定义
每一步都做出当前看来最优的操作。
问题引入——活动选择问题
问题描述
活动选择问题就是对给定的包含n个活动的集合S，在已知每个活动开始时间和结束时间的条件下，从中选出最多可兼容活动的子集合，称为最大兼容活动集合。 不失一般性，设活动已经按照结束时间单调递增排序。
分析
这个问题具有最优子结构，可以用动态规划，但用贪心复杂度更低。
实际上，任何一个可以用贪心解决的问题都可以用动态规划解决。
这里的贪心策略为：每次都选择能选择的活动中结束时间最早的活动。
证明贪心正确性：
感性上，这样做可以为后面留出最多的时间。
严格证明，只需证明如下定理：
考虑任意非空子问题
，令
是
证明：
设
为
。
若
，则成立。
若
，则设
，由于
也是
，故
证毕。
实现
自顶向下
自底向上
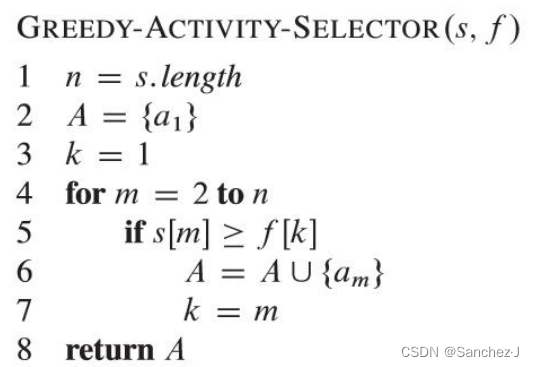
总结——贪心算法的一般步骤
1）确定问题的最优子结构；
2）将最优化问题转化为这样的形式：每次对其作出选择后，只剩下一个子问题需要求解；
3）证明作出贪心选择后，剩余的子问题满足：其最优子解与前面的贪心选择组合即可得到原问题的最优解(具有最优子结构)。
总结——证明贪心算法正确性
贪心选择性质和最优子结构性是两个关键要素。
贪心选择性质：可以通过做出局部最优（贪心）选择来构造全局最优解的性质。
贪心选择性质使得我们进行选择时，只需做出当前看起来最优的选择，而不用考虑子问题的解。
例子——Huffman编码
Huffman算法
从 |C| 个叶子结点开始，每次选择频率最低的两个结点合并，将得到的新结点加入集合继续合并，这样执行 |C|-1次 “合并” 后即可构造出一棵编码树——Huffman树。
（采用以freq为关键字的最小优先队列Q，提取两个最低频率的对象将之合并。）
时间复杂度分析
假设Q使用最小二叉堆实现，则：
首先，Q的初始化时间复杂度O(n)。
其次，循环的总代价是O(nlgn)：for循环共执行了n-1次，每次从堆中找出当前频率最小的两个结点及把合并得到的新结点插入到堆中均花费O(lgn)，所以循环的总代价是O(nlgn)。
总时间复杂度O(nlgn)。
正确性证明
首先，可以发现，一个最优字符编码方案总对应一棵满 (full) 二叉树， 即每个非叶子结点都有两个孩子结点。
引理1
令C为一个字母表，其中每个字符 c∈C 都有一个频率 c.freq。 令 x 和 y 是C中频率最低的两个字符。那么存在C的一个最优前缀码，x和y的码字长度相同，且只有最后一个二进制位不同。
证：
令T是一个最优前缀码所对应的编码树，a和b是T中深度最大的兄弟叶结点。 不失一般性，假设 a.freq ≤ b.freq 且 x.freq ≤ y.freq。
由于x和y是叶结点中频率最低的两个结点，所以应有 x.freq ≤ a.freq 且y.freq ≤ b.freq。
若 x.freq = b.freq，则有a.freq = b.freq = x.freq = y.freq，此时引理成立。
若 x.freq ≠ b.freq，即 x≠ b。则在T中交换 x 和 a，生成一棵 新树T’ ；然后再在T’中交换 b和y，生成另一棵新树T” ，那么在T”中x和y是深度最深的两个兄弟结点。
计算代价差：
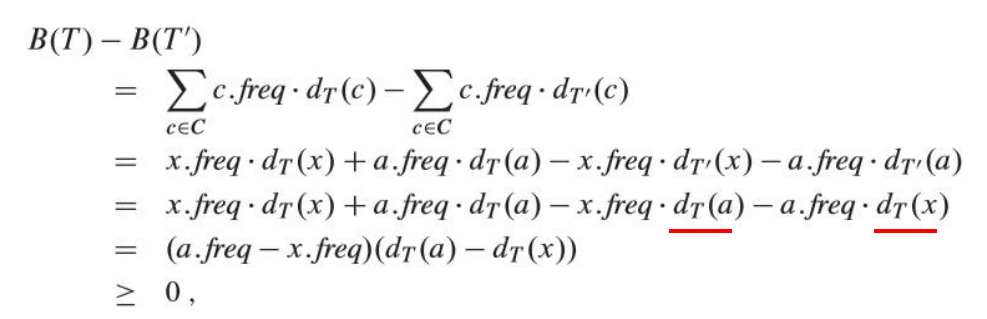
同理有
因此，又B(T)为最优编码，故
即得证：T” 也是最优解，且 x 和 y 是其中深度最大的两个兄弟结点，x和y的码字长度相同，且只有最后一个二进制位不同。
引理2
令C为一个给定的字母表，其中每个字符c∈C都有一 个频率c.freq。x和y是C中频率最低的两个字符。
令C'为C去掉字符x和y，并加入一个新字符z后得到的字母表， 即C' = C - {x, y}∪{z}，z.freq= x.freq + y.freq。 令T'为字母表C'的任意一个最优前缀码对应的编码树。
则有：可以将T'中叶子结点 z 替换为一个以x和y为孩子的内部结点，得到树T，而T表示字母表C的一个最优前缀码。
由引理1、2可得Huffman算法的正确性。
![[PyTorch][chapter 9][李宏毅深度学习][CNN]](https://img-blog.csdnimg.cn/direct/ee1281c966204a209c3204c8f2113047.png)
