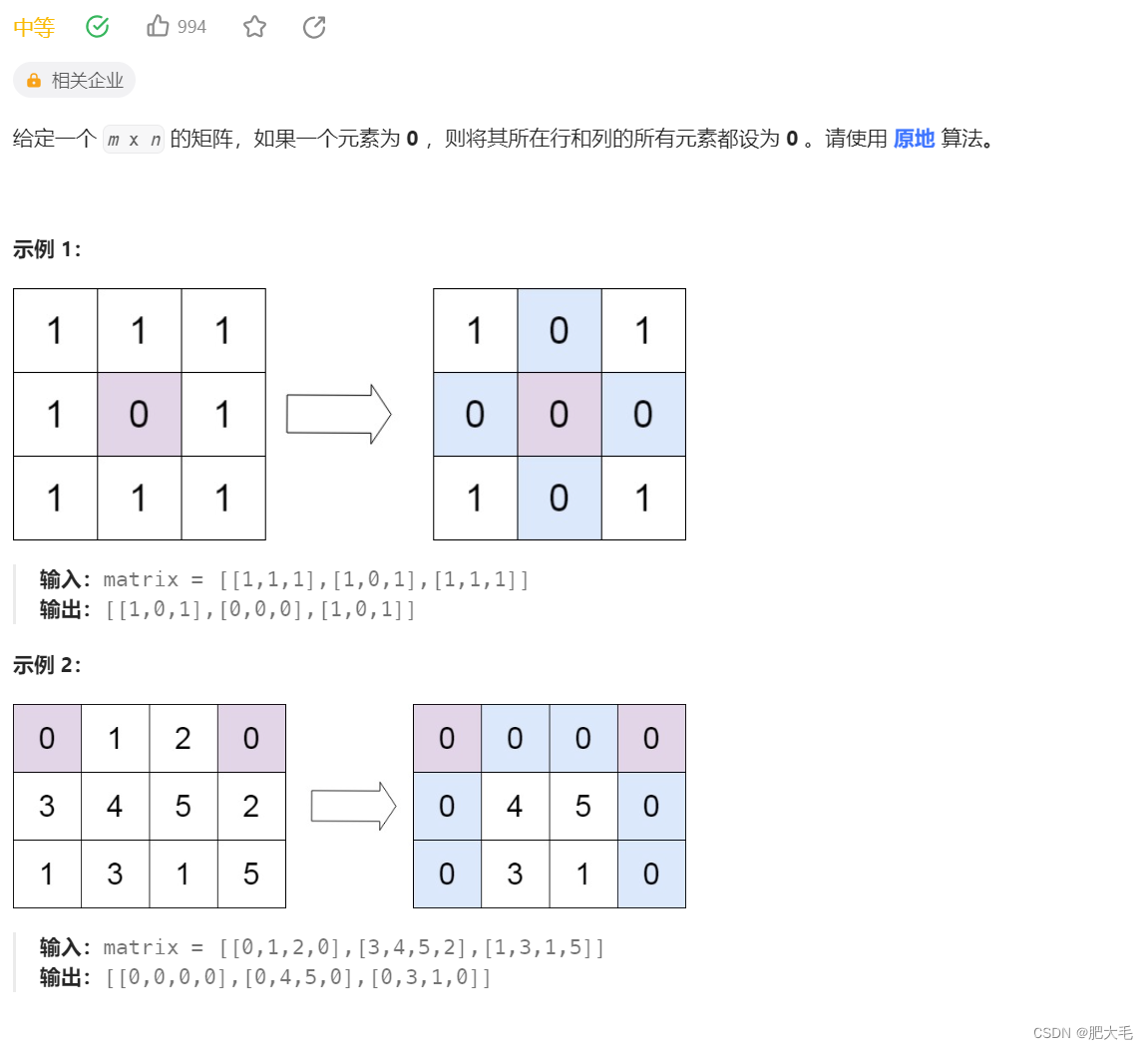
解题思路：

本题要求原地置换元素
对矩阵进行第一轮遍历，使用第一行第一列来充当该行该列是否要置换为0的标记位，如果第一行或第一列本身就含有零元素，我们使用colZero和rowZero变量来对其标记。如果第i行第j列的那个元素为0，我们就将[i][0]和[0][j]的元素置换为0，接着判断i和j是否为0，即第一行第一列，如果是，则colZero和rowZero都赋值为true。
对矩阵进行第二轮遍历：即对不包含第一行或第一列进行处理，根据第一轮遍历得到的标记将对应的行和列中的元素置换为0。
对矩阵进行第三轮遍历：即对第一行和第一列本身就含有0元素的情况进行处理，如果第一行或者第一列本身就包含0元素，则将其对应的行或列元素都置换为0。

代码实现：

 public void setZeroes(int[][] matrix) {
        int m=matrix.length;
        int n=matrix[0].length;
        boolean colZero=false;//第一行是否有0
        boolean rowZero=false;//第一列是否有0
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(matrix[i][j]==0)
                {
                    matrix[0][j]=matrix[i][0]=0;//标记位
                    //判断是否第一行第一列为0
                    if(i==0) rowZero=true;
                    if(j==0) colZero=true;
                }
            }
        }

        //第二轮遍历，将标记的行和列置换为0
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                if(matrix[i][0]==0 || matrix[0][j]==0)
                {
                    matrix[i][j]=0;
                }
            }
        }

        //如果第一行或第一列本来就有0，则进行0置换
        for(int i=0; colZero && i<m;i++) matrix[i][0]=0;
        for(int j=0; rowZero && j<n;j++) matrix[0][j]=0;
    }