李沐机器学习系列1--- 线性规划

1 Introduction

1.1 线性回归函数

典型的线性回归函数
$f(x)=\vec{w} \cdot \vec{x}$
现实生活中，简单的线性回归问题很少，这里有一个简单的线性回归问题。房子的价格和房子的面积以及房子的年龄假设成线性关系。
$price = w_{area}*area + w_{age}+b$

1.2 损失函数

确定了变量和结果之间的大致关系以后，我们需要通过优化的方法进行迭代优化求解。
让我们从优化的角度来看这个问题。
$0.5\sum_i^n(\vec{w}*x-y^{i})^TQ(\vec{w}*x-y^{i})$
这是一个典型的QP问题，可以使用迭代的方法找到最优解。
在QP问题中，往往采用wolfe规则，但是这往往使用到全部的数据，在大规模的机器没有办法这么做，采用SGD的方法。

1.3 随机梯度下降

对于方程求解问题，典型的方法是牛顿迭代法。
基础的牛顿迭代法可以这么理解：
$\begin{aligned} 0-f(x_i) &=f'(x_i)(x_{i+1}-x_i) \\ x_{i+1}&=x_i-\frac{f(x_i)}{f'(x_i)} \end{aligned}$
对于这个符号，从直觉的角度理解，对于一个单调函数，如果f(x_i)和f’(x_i)要是同方向，就会离稳态越来越远，所以需要添加符号来保持稳态。使用简单的牛顿迭代法，参数会变化太大，所以在步长的选择上，有很多trick。
对于一个凸函数来说，梯度方向是让函数值升高的最快方向，对于一个非凸函数，梯度方向可能会导致求解进入局部最大值或者鞍点。
$\begin{aligned} w' &=w-\lambda f'(x) \\ w' &= w-\frac{\lambda}{\beta}\sum_{i\in \beta}x^{(i)}(w^Tx^{(i)}+b -y^{(i)}) \\ b' & = b-\frac{\lambda}{\beta}\sum_{i\in \beta}(w^Tx^{(i)}+b -y^{(i)}) \\ \end{aligned}$

在这里插入图片描述

1.3 正态分布与平方损失

每个参数可能会有一定的噪声，噪声正态分布如下：
$\begin{aligned} y &=\vec{w}^T\vec{x}+b+\epsilon \\ \epsilon& \in N(0, \sigma^2) \end{aligned}$

给定的x观察到特定的y的似然
$\begin{aligned} p(y|x)&=\frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{1}{2\sigma^2}(y-\vec{w}^T\vec{x}-b)^2) \end{aligned}$
每个点都是独立同分布
$P(y|X)=\prod_{i=1}^n(p(y^{i}|x^i))$
进行对数
$-logP(y|X)=\sum_{i=1}^n0.5log(2\pi \sigma^2)+\frac{1}{2\sigma^2}(y^i-w^Tx^i-b)^2$

2 线性回归从零开始实现

2.1 生成数据

def generate_data(w, b, num_examples):
	x = torch.norm(0, 1, (num_examples, len(w)))
	y = torch.matmul(w, x) + b
	y += torch.norm(0, 0.01, y.shape())
	return x, y.reshape((-1, 1))

2.2 batch size data selector

def data_iter(features, labels, batch_size=10):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i:min(i + batch_size, num_examples)])
        yield(features[batch_indices], labels[batch_indices]

2.3 定义网络和loss

sgd 和优化中的方法的区别，sgd利用部分样本，采用迭代的方式，进行优化；传统的优化方法，如qp或者sqp则对全部的样本的loss进行迭代，并且迭代过程中，会同时优化步长；

def linreg(x, w, b):
    y = torch.matmul(x, w) + b
    return y

def loss(y_hat, y):
    l = 0.5 * (y - y_hat) ** 2
    return l

w = torch.normal(0, 0.1, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
def sgd(params, lr, batch_size):
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

一定要在参数更新这里将param.grad.zero_()

2.4 进行训练

num_epochs = 3
net = linreg
lr = 0.02
batch_size = 10
for epoch in range(num_epochs):
    for x, y in data_iter(features, labels, batch_size):
        l = loss(y, net(x, w, b))
        l.sum().backward()
        sgd([w, b], lr, batch_size) 
    with torch.no_grad():
        predicted = net(features, w, b)
        mse = ((predicted - labels) ** 2).mean()
        print("epoch ", epoch, " MSE: ", mse.item())

3 使用pytorch进行简化

3.1 数据选择器

# 定义迭代器
def data_selector(data_arrays, batch_size, is_train=True):
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = data_selector((features, labels), batch_size, True)

3.2 网络

# 定义各种函数
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))
# 初始化数值
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# 定义损失函数
loss = nn.MSELoss()
# 使用优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

采用框架，参数被封装在了net中，在定义sgd训练，使用net.parameters()传递参数

3.3 训练

num_epochs = 3
for epoch in range(num_epochs):
    for x, y in data_iter:
        l = loss(net(x), y)
        trainer.zero_grad()
        l.sum().backward()
        trainer.step()
    l = loss(net(x), y)
    print(f'epoch {epoch}, loss {l: f}')

4 softmax

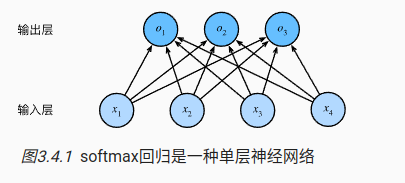
在这里插入图片描述
我们在机器学习中经常会遇到分类问题，每个种类都自己的预测结果。
$\vec{o}=\vec{W}\vec{x}+\vec{b}$

4.1 softmax运算

如果只是这样简单的全连接层计算，会产生一个问题，输出的累计和并不等于1。但是我们的标签的总和是1.
为了让总和为1，每项的输出范围为[0,1]，并且使用exp求导的时候更加简单
$softmax(x)=\frac{exp(\vec{o}_i)}{\sum_{i=0}^n(exp(\vec{o}_i))}$
我们在做决策的时候，输出最大概率项
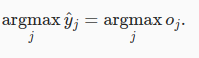
在这里插入图片描述

4.2 损失函数

使用最大似然估计
$-logP(Y|X)=\sum_{i=1}^n-logP(y^{(i)}|x^{(i)})=\sum_{i=1}^nl(y^{(i)},\hat{y}^{(i)})$
理解不了，以后再说。

熵
知道真实概率的人所经历的惊异程度
$H[P]=\sum_j-P(j)logP(j)$

4.3 训练代码

数据

# 使用pytorchvision 下载数据
# iterator
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
    root="../data", train=False, transform=trans, download=True)

image, label = mnist_train[0]

train_iter = data.DataLoader(mnist_train, 32, shuffle=True,
                            num_workers=4)
test_iter = data.DataLoader(mnist_test, 32, shuffle=True,
                            num_workers=4)
for x, y in train_iter:
    break

定义网络结构
这里要注意，pytorch上，采用nnum_inputs这种输入结构，输出结构1num_outputs

# 定义网络结构，输入结构是o=W*x+b, x是[n * 784], w = 784 * 10, b = 1 * 10
num_inputs = 784
num_outputs = 10
w = torch.normal(0, 0.01, (num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
print(w.shape, b.shape)

定义softmax函数

# 定义关键函数softmax, 两个样本
x = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
y = torch.tensor([0, 2])
print(x[[0, 1], y])
# -log,这里的keepdim非常关键，这样才能保证两个数组的维度相同，可以对应上
def softmax(x):
    x_exp = torch.exp(x)
    partition = x_exp.sum(axis=1, keepdim=True)
#     print(partition.shape)
    return x_exp / partition

p_x = softmax(x)
print(p_x)

定义loss

# 自定义模型
# 这里需要对x进行reshape，因为x很可能是乱的，需要reshape成n*num_inputs这种类型的
def net(x):
    return softmax(torch.matmul(x.reshape((-1, w.shape[0])), w) + b)

# 定义损失函数
# 这里采用了小技巧，二维数组中，使用两个等长的向量，可以快捷的索引元素
def crossEntropy(y_hat, y):
    return -torch.log(y_hat[range(len(y_hat)), y])

y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
crossEntropy(y_hat, y)

评估训练中的精度

# 记录分类精度， 用argmax(y_hat)==y, 记录是否正确
def accuracy(y_hat, y):
    # 防止y_hat采用概率, 并且有多个类别
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

# 用总数和预测值进行比较
accuracy(y_hat, y) / len(y)

#创建一个通用的评估器
class Accumulator:
    def __init__(self, n):
        self.data = [0.0] * n
    # 解决各种不同类型元素累加的trick
    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]
    def reset(self):
        self.data = [0.0] * len(self.data)
    def __getitem__(self, i):
        return self.data[i]

def evaluate_accuracy(net, data_iter):
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metrics = Accumulator(2)
    with torch.no_grad():
        for x, y in data_iter:
            metrics.add(accuracy(net(x), y), y.numel())
    return metrics[0] / metrics[1]

evaluate_accuracy(net, test_iter)

进行训练

#进行训练
lr = 0.1
def updater(batch_size):
    return d2l.sgd((w, b), lr, batch_size)

def train_epoch_ch3(net, train_iter, loss, updater):
    if isinstance(net, torch.nn.Module):
        net.train()
    metric = Accumulator(3)
    for x, y in train_iter:
        y_hat = net(x)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            l.sum().backward()
            updater(x.shape[0])
        metric.add(l.sum(), accuracy(y_hat, y), y.numel())
    return metric[0] / metric[2], metric[1] / metric[2]

其他内容

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

进行训练

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc
    
num_epochs = 10
train_ch3(net, train_iter, test_iter, crossEntropy, num_epochs, updater)

4.4 softmax 的简洁实现

通过softmax 函数得到每项的概率时
$\hat{y}_j=\frac{exp(o_j)}{\sum_kexp(o_k)}$
为了避免太大的数，造成数据的上溢，将特别大的项减掉
$\hat{y}_j=\frac{exp(o_j - max(o_k))}{\sum_kexp(o_k-max(o_k))}$
这样会造成某一些数会非常小，接近0，在计算交叉熵时， $y_ilog\hat{y}_i$ 会出现无穷小的情况，计算交叉熵时有一个小技巧
$log(\hat{y}_i)=o_j-max(o_k)-log(\sum_kexp(o_k-max(o_k)))$

使用pytorch 完整的代码实现

import torch
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader


transform = transforms.ToTensor()
train_dataset = torchvision.datasets.MNIST(root='./data', 
                                           train=True, 
                                           transform=transform, 
                                           download=True)
test_dataset = torchvision.datasets.MNIST(root='./data', 
                                          train=False, 
                                          transform=transform)

batch_size = 256
train_iter = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_iter = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
loss = nn.CrossEntropyLoss(reduction='mean')
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
num_epochs = 10

for epoch in range(num_epochs):
    total_loss = 0.0  # 初始化总损失为零
    for x, y in train_iter:
        # 前向传播
        output = net(x)
        l = loss(output, y)

        # 反向传播
        trainer.zero_grad()
        l.backward()
        trainer.step()

        # 累加批次的损失
        total_loss += l.item()  # 使用 l.item() 将损失转换为 Python 数字

    # 计算整个 epoch 的平均损失
    average_loss = total_loss / len(train_iter)
    
    # 打印当前轮的平均损失
    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {average_loss:.4f}')

Epoch [1/10], Loss: 1.0835
Epoch [2/10], Loss: 0.6061
Epoch [3/10], Loss: 0.5108
Epoch [4/10], Loss: 0.4644
Epoch [5/10], Loss: 0.4364
Epoch [6/10], Loss: 0.4164
Epoch [7/10], Loss: 0.4017
Epoch [8/10], Loss: 0.3903
Epoch [9/10], Loss: 0.3814
Epoch [10/10], Loss: 0.3728