论文阅读和复现：去除PPG运动伪影的IEEE论文

news2024/12/25 9:58:30

论文阅读和代码复现：
《Combining Nonlinear Adaptive Filtering and Signal Decomposition for Motion Artifact Removal in Wearable Photoplethysmography》

基本介绍：

由于手腕运动造成的噪声：运动伪影，使得PPG方法的心率监测不准，去除运动伪影噪声在智能手表中是一个难点。

论文中使用的开源数据：PPG database used in 2015 IEEE Signal Processing Cup[1]

[1]Pace and Bricout, “Low Heart Rate Response of Children with Autism Spectrum Disorders in Comparison to Controls during Physical Exercise,” Physiology & Behavior, vol.141, pp.63-68, 2015.

目前已经有的研究：

使用独立成分分析ICA

ICA有一个关键的统计独立或不相关假设[11]。因此，在许多实际场景中，将MA与PPG信号分离的结果并不令人满意。

[11]J. Yao and S. Warren, “A short study to assess the potential of independent component analysis for motion artifact separation in wearable pulse oximeter signals,” in Proc. 27th Annual Conf IEEE Engg. Medicine and Biology, pp. 3585-3588, 2005.

使用自适应滤波

通过适当设计参考信号，在某些情况下可以达到令人满意的效果。然而，一个设计不好的参考信号会导致较差的MA去除性能。此外，原始PPG信号中的MA与参考信号之间的关系可能不是线性相关的，而是非线性相关的，当选择同步加速度信号作为参考信号时。

[12] Comtois Gary, Yitzhak Mendelson, and Piyush Ramuka, “A Comparative Evaluation of Adaptive Noise Cancellation Algorithms for Minimizing Motion Artifacts in a Forehead-Mounted Wearable Pulse Oximeter,” 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pp.1528-1531, 2007.
[13] A. B. Barreto, L. M. Vicente, and I. K. Persad, “Adaptive Cancellation of Motion Artifact in Photoplethysmographic Blood Volume Pulse Measurements for Exercise Evaluation,” Engineering in Medicine and Biology Society, IEEE 17th Annual Conference, vol.2, pp.983-984. 1995.
[14] Ram, M. Raghu, et al. “A novel approach for motion artifact reduction in PPG signals based on AS-LMS adaptive filter.” IEEE Transactions on Instrumentation and Measurement, pp. 1445-1457, 2012.
[15] Hyonyoung Han and Jung Kim, “Artifacts in wearable photoplethysmographs during daily life motions and their reduction with least meansquare based active noise cancellation method,” Computers in Biology and Medicine 42, pp. 387-393, 2012.
[16] Asada, H. Harry, Hong-Hui Jiang, and Peter Gibbs, “Active noise cancellation using MEMS accelerometers for motion-tolerant wearable bio-sensors,” Engineering in Medicine and Biology Society, 2004. IEMBS’04. 26th Annual International Conference of the IEEE. vol. 1, 2004.

使用信号分解

信号分解[17]，[18]最近被证明是一种有效的去除MA的方法。例如，在[17]中，作者使用奇异谱分析(SSA)将原始PPG分解为多个分量，然后使用同步加速度信号的信息来识别与MA相关的分量。去除这些分量后，利用剩余分量重构PPG信号，得到更清晰的PPG信号。同样，在[18]中，使用经验模态分解(EMD)将一个原始PPG信号分解为许多分量，并使用同步加速度信号的频谱进行频谱减法去除与MA相关的分量。然而，信号分解通常具有较大的计算量，这可能会阻碍其在低功耗可穿戴设备中的应用。

[17] Z. Zhang, Z. Pi, and B. Liu, “TROIKA: A general framework for heart rate monitoring using wrist-type photoplethysmographic signals during intensive physical exercise,” IEEE Transactions on Biomedical Engineering, vol. 62, no. 2, pp. 522-531, 2015.

[18] Y. Zhang, B. Liu, Z. Zhang, “Combining Ensemble Empirical Mode Decomposition with Spectrum Subtraction Technique for Heart Rate Monitoring Using Wrist-Type Photoplethysmography,” Biomedical Signal Processing and Control, vol. 21, pp. 119-125, 2015.

论文的算法方案

在这里插入图片描述

基本步骤：

1、PPG传感器和加速度传感器同时采集原始数据；并且对数据进行带通滤波处理，PPG数据的通带选择0.4-5.0 HZ；

2、A：Volterra RLS 非线性滤波算法处理PPG数据，其中的加速度数据作为Volterra RLS的参考信号；

3、判断Volterra RLS滤波结果是否满足要求，根据相关性的阈值进行判断；

4、第3步的判断满足要求YES，则进入到步骤6，谱峰追踪算法；No则进入步骤5；

5、SSA进行进一步处理PPG数据，去除运动伪影；

6、谱峰追踪，原因是即使进行运动伪影的处理，在FFT算法处理PPG信号后，得到的频谱的最大幅值对应的频率不一定是心率值，运动伪影太强会导致出现多个谱峰，而且运动伪影造成的谱峰比心率峰值还要大的现象。这里需要使用机器学习算法或专家经验（例如两个时间窗之间的心率不会突变）进行谱峰选取；

7、最终计算得到心率值；

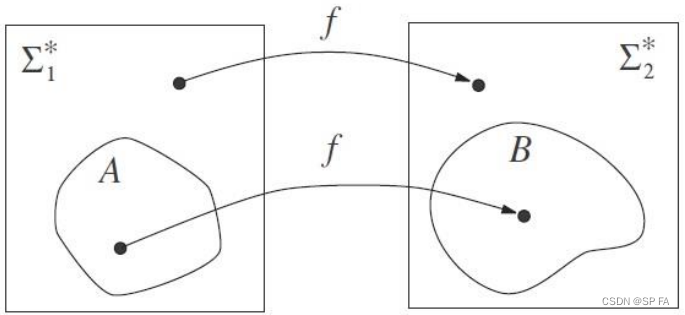
Volterra-RLS去除运动伪影算法原理

在这里插入图片描述

如图所示。基于RLS volterra的非线性自适应滤波系统框图。它有两个输入。一个是原始PPG信号s(k)，包含感兴趣的信号s1(k)和加上干扰n(k)。另一个输入是加速度数据xk。对噪声进行过滤，以产生与n(k)尽可能接近的副本的输出n(k)。这个输出从主要输入s(k)中减去，得到系统输出ε(k)。

代码基本实现Volterra-RLS算法去除运动伪影：

算法流程参考：
Paulo S. R. Diniz (auth.) - 《Adaptive Filtering_ Algorithms and Practical Implementation》-Springer US (2013)

在这里插入图片描述

根据作者介绍可知，Volterra RLS算法和传统的RLS算法的区别就是输入 $\pmb{x}(k)$ 。其中 $\pmb{x}(k)$ 如下所示：其中N是指滤波器的阶数。

在这里插入图片描述

# -*- coding: utf-8 -*-
#
# Copyright (C) 2022 Emperor_Yang, Inc. All Rights Reserved 
#
# @CreateTime    : 2022/12/31 8:00
# @Author        : Emperor_Yang 
# @File          : volterra_rls.py
# @Software      : PyCharm

import numpy as np
import queue


class PPGAccData(object):
    def __init__(self):
        self._ppg = []
        self._acc = []

    def push_data(self, ppg_data, acc_data):
        assert (len(ppg_data) == len(acc_data))  # 保证ppg和acc数据是长度一致的
        self._ppg.append(ppg_data)
        self._acc.append(acc_data)

    def get_data(self, data_len):
        ppg_data = []
        acc_data = []
        current_ppg_data_len = len(self._ppg)
        if len(self._ppg) > data_len:
            ppg_data = self._ppg[-data_len: -1]
            acc_data = self._acc[-data_len: -1]
        else:
            for i in range(data_len - current_ppg_data_len):
                ppg_data.append(0)
                acc_data.append(0)
            ppg_data.append(self._ppg)
            acc_data.append(self._acc)
        return np.array(ppg_data), np.array(acc_data)


N = 10  # 滤波算法的阶数
delta = 10  # signal power
matrix_size = (N + 1) * (N + 1) + (N + 1)
S_D_init = delta * np.ones((matrix_size, matrix_size))
x_init = np.zeros((matrix_size, 1))
w_init = np.zeros((matrix_size, 1))
lambda_value = 0.1  # (0, 1)

ppg_acc_data = PPGAccData()
ppg_data, acc_data = ppg_acc_data.get_data(N)
x = x_init
S_D = S_D_init
w = w_init

stop_flag = True

while stop_flag:
    e = acc_data - np.transpose(x) @ w
    pha_matrix = S_D @ x
    S_D = 1 / lambda_value * (
                S_D - (pha_matrix @ np.transpose(pha_matrix) / lambda_value + np.transpose(pha_matrix) @ x))
    w = w + e @ S_D @ x
    y = np.transpose(w) @ x
    delta_vector = acc_data - y
    ppg_data, acc_data = ppg_acc_data.get_data(N)
    x = ppg_data
    d = acc_data