C++实现哈希表。

news2024/9/20 0:52:05

目录

一. unordered_map unordered_set 和 map set的区别

二. 哈希

1. 哈希，哈希表，哈希函数。

2. 哈希冲突。

3. 哈希函数补充

3. 解决哈希冲突的两大方法：闭散列，开散列

闭散列

闭散列实现代码：

闭散列的删除问题：

负载因子：

开散列：

开散列哈希表代码实现：

开散列的负载因子和扩容问题：

开散列和闭散列的比较：

一. unordered_map unordered_set 和 map set的区别

1. map set底层采取的红黑树的结构，unordered_xxx 底层数据结构是哈希表。unordered_map容器通过key访问单个元素要比map快，但它通常在遍历元素子集的范围迭代方面效率较低。

2. Java中对应的容器名为 HashMap HashSet TreeMap TreeSet，命名方面比C++好了很多。主要是早期C++并没有实现哈希结构的容器（C++11之前），也就是unordered系列，在C++11中新增了unordered_map，unordered_set，unordered_multimap，unordered_multiset，故因为历史命名问题，取了这样的名字。

3. 它们的使用大体上几乎一致。显著的差别是：
a、map和set为双向迭代器，unordered_xxx和是单向迭代器。
b、map和set存储为有序存储（红黑树结构，中序遍历有序），unordered_xxx为无序存储（哈希表的结构致使）

4. 性能差异：采取哈希表的unordered系列容器在大量数据的增删查改效率更优，尤其是查（搜索）

二. 哈希

1. 哈希，哈希表，哈希函数。

哈希的思想是：将元素的关键码与元素在哈希表中的存储位置构建某种函数关系，使得查找时，可以通过这个函数，直接获取元素的存储位置。对比顺序表和搜索树，顺序表需要将关键码一一对比，时间复杂度为O(N)，而搜索树这样的结构，时间复杂度也是(log_2 N)，取决于元素个数，树的高度，同样需要若干次比较。而哈希可以使得查找元素的存储位置不需要比较，直接通过函数获取。

将这个转换函数成为哈希函数（散列函数），得到的元素的存储位置成为哈希地址（也就是在哈希表中的下标，哈希表一般为顺序表结构），将构造出的数据结构成为哈希表（散列表）。

2. 哈希冲突。

难免有某些元素的不同关键码通过同一个哈希函数转换后得到的哈希地址相同，这种现象称为哈希冲突或哈希碰撞。

故，要想构造出理想的哈希存储结构，必须解决哈希冲突，合理安排那些关键码不同，而哈希地址相同的元素。

3. 哈希函数补充

哈希函数有很多种，也就是将元素的关键码，转换为元素存储位置的函数。哈希函数的设计越精妙，产生哈希冲突的概率越低，但是无法完全避免哈希冲突。

下方哈希表的实现代码中，采取的哈希函数为除留余数法，即将关键码取模哈希表的长度，获取哈希地址。

3. 解决哈希冲突的两大方法：闭散列，开散列

闭散列

闭散列：也叫开放定址法。核心思想比较简单：若某两个元素发生哈希冲突，第二个得到该哈希地址的元素插入时，将该元素存放到哈希表中发生哈希冲突的“下一个”空位置中去。其实也就是再找一个空位置，然后插入。

如何寻找下一个“空位置”的方法有两种，1. 线性探测，即从哈希地址处起，逐个位置进行判断，直到找到空位置。2. 二次探测：第一次看hashAdd+0^2下标处有没有被占用（设哈希地址为hashAdd。其实也就是看获取的哈希地址处有没有没被占用），第二次看hashAdd+1^2，第三次看hashAdd+2^2，直到找到没有被占用的位置。

相比于线性探测，二次探测只是将发生哈希冲突的元素的存储位置分离一些，不像线性探测一样连续存储，能一定程度减少哈希冲突带来的性能损耗，但是不能根本解决问题。

闭散列实现代码：

// 开散列（链地址法）解决哈希表中的哈希冲突
namespace OpenHashing
{
    // 这里仅仅是实现哈希表的最简单逻辑，Find等函数的实现没有考虑unordered_map等容器
    template <class K, class V>
    struct HashNode
    {
        HashNode<K,V>(const pair<K,V>& kv)
        :_kv(kv)
        { }
        pair<K, V> _kv;
        HashNode* _next = nullptr;
    };

    template <class K>
    struct HashAddressConvert
    {
        size_t operator()(const K& key) {
            return key;
        }
    };

    // 模板特化
    template <>
    struct HashAddressConvert<string>
    {
        size_t operator()(const string& str) {
            size_t sum = 0;
            for(auto&ch:str)
            {
                sum*=131;
                sum+=ch;
            }
            return sum;
        }
    };

    template <class K, class V, class HDC = HashAddressConvert<K>>
    class HashTable
    {
        typedef HashNode<K, V> Node;
    public:
        ~HashTable() {
            for(auto& ptr : _table) {
                Node* cur = ptr;
                while(cur) {
                    Node* next = cur->_next;
                    delete cur;
                    cur = next;
                }
                ptr = nullptr;
            }
        }
        bool Insert(const pair<K, V>& kv) {
            if(Find(kv.first)) {
                return false;
            }
            HDC convert;
            if(_table.size() == 0 || 10 * _size / _table.size() >= 10) {
                // 开散列法哈希表扩容
                vector<Node*> newTable;
                size_t newSize = _table.size() == 0 ? 10 : _table.size()*2;
                newTable.resize(newSize);
                for(size_t i = 0; i < _table.size(); ++i) {
                    Node* cur = _table[i];
                    while(cur) {
                        Node* next = cur->_next;
                        size_t hashAddress = convert(cur->_kv.first) % newTable.size();
                        cur->_next = newTable[hashAddress];
                        newTable[hashAddress] = cur;
                        cur = next;
                    }
                    _table[i] = nullptr;
//                    if(_table[i]) {
//                        Node* cur = _table[i];
//                        Node* next = cur->_next;
//                        while(cur) {
//                            size_t hashAddress = convert(cur->_kv.first) % newTable.size();
//                            cur->_next = newTable[hashAddress];
//                            newTable[hashAddress] = cur;
//                            cur = next;
//                            if(cur)
//                                next = cur->_next;
//                        }
//                        // 也没必要其实
//                        _table[i] = nullptr;
//                    }
                }
                _table.swap(newTable);
            }
            // 通过哈希函数求哈希地址
            size_t hashAddress = convert(kv.first) % _table.size();
            Node* ptr = _table[hashAddress];
            Node* newNode = new Node(kv);
            // 每个哈希桶中进行头插
            newNode->_next = ptr;
            _table[hashAddress] = newNode;
            ++_size;
            return true;
        }

        Node* Find(const K& key) {
            if(_table.size() == 0) {
                return nullptr;
            }
            HDC convert;
            size_t hashAddress = convert(key) % _table.size();
            Node* cur = _table[hashAddress];
            while(cur) {
                if(cur->_kv.first == key) {
                    return cur;
                }
                cur = cur->_next;
            }
            return nullptr;
        }

        bool Erase(const K& key) {
            if(_table.size() == 0)
                return false;
            HDC convert;
            size_t hashAddress = convert(key) % _table.size();
            Node* cur = _table[hashAddress];
            Node* prev = nullptr;
            while(cur) {
                if(cur->_kv.first == key) {
                    if(prev)
                        prev->_next = cur->_next;
                    else
                        _table[hashAddress] = cur->_next;
                    delete cur;
                    --_size;
                    return true;
                }
                prev = cur;
                cur = cur->_next;
            }
            // 不存在该节点
            return false;
        }

        // 哈希表的长度
        size_t TableSize() {
            return _table.size();
        }

        // 非空哈希桶的个数
        size_t BucketNum() {
            size_t num = 0;
            for(auto&ptr:_table) {
                if(ptr)
                    num++;
            }
            return num;
        }

        // 哈希表中数据的个数
        size_t Size() {
            return _size;
        }

        // 最大的桶的长度
        size_t MaxBucketLength() {
            size_t max = 0;
            for(size_t i = 0; i < _table.size(); ++i) {
                size_t len = 0;
                Node* ptr = _table[i];
                while(ptr)
                {
                    len++;
                    ptr = ptr->_next;
                }
                if(len > max)
                    max = len;
//                if (len > 0)
//                    printf("[%d]号桶长度:%d\n", i, len);
            }
            return max;
        }
    private:
        vector<HashNode<K, V>*> _table;
        size_t _size = 0;
    };

}

闭散列的删除问题：

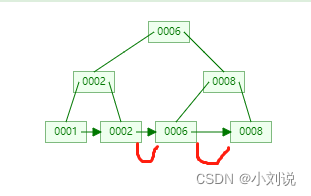
如上哈希表中，关键值4和44采取除留余数法哈希函数获取的哈希地址相同，都是4，最后插入44时，向后找空位置，无论是线性探测还是二次探测，都会插入到哈希表中哈希地址（下标）为8处。

此时，若删除5（或者4，6，7），再查找44，就会影响44的查找，故在闭散列的哈希表实现中，哈希表中每个存储位置的存储状态，包括：存在EXIST，删除DELETE，空EMPTY。查找44时，不能因为5位置为空就停止线性探测查找，也就是遇到DELETE不停。（看代码）。线性探测采用标记的伪删除法来删除一个元素。

负载因子：

负载因子为哈希表中的元素个数/哈希表长度。

负载因子越大，同样长度的哈希表存储的元素越多，发生哈希冲突概率越大，查找时效率越低，但是空间使用率越高。

负载因子越小，同样长度的哈希表存储的元素越少，发生哈希冲突概率越小，查找时效率越高，但是空间使用率越低。

理论上，采取闭散列的哈希表的最大负载因子为1，负载因子为1时必须扩容。但是，闭散列哈希表当负载因子超过0.8时，查表时CPU缓存不命中按照指数曲线上升。故，负载因子需要取一个合适的值，对于闭散列（开放定址法）的哈希表，负载因子非常重要，应控制在0.7 ~ 0.8以下，若超出，即需要扩容哈希表。

开散列：

开散列是另一种解决哈希冲突的方法。核心思想是：首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码（发生哈希冲突）归于同一子集合，每一个子集合称为一个哈希桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

哈希表代码实现中，哈希表数组存储的是结点指针（结点封装数据和单链表next指针）。

开散列的哈希表中每个哈希桶存放的都是发生哈希冲突的元素。

开散列哈希表代码实现：

// 开散列（链地址法）解决哈希表中的哈希冲突
namespace OpenHashing
{
    // 这里仅仅是实现哈希表的最简单逻辑，Find等函数的实现没有考虑unordered_map等容器
    template <class K, class V>
    struct HashNode
    {
        HashNode<K,V>(const pair<K,V>& kv)
        :_kv(kv)
        { }
        pair<K, V> _kv;
        HashNode* _next = nullptr;
    };

    template <class K>
    struct HashAddressConvert
    {
        size_t operator()(const K& key) {
            return key;
        }
    };

    // 模板特化
    template <>
    struct HashAddressConvert<string>
    {
        size_t operator()(const string& str) {
            size_t sum = 0;
            for(auto&ch:str)
            {
                sum*=131;
                sum+=ch;
            }
            return sum;
        }
    };

    template <class K, class V, class HDC = HashAddressConvert<K>>
    class HashTable
    {
        typedef HashNode<K, V> Node;
    public:
        ~HashTable() {
            for(auto& ptr : _table) {
                Node* cur = ptr;
                while(cur) {
                    Node* next = cur->_next;
                    delete cur;
                    cur = next;
                }
                ptr = nullptr;
            }
        }
        bool Insert(const pair<K, V>& kv) {
            if(Find(kv.first)) {
                return false;
            }
            HDC convert;
            if(_table.size() == 0 || 10 * _size / _table.size() >= 10) {
                // 开散列法哈希表扩容
                vector<Node*> newTable;
                size_t newSize = _table.size() == 0 ? 10 : _table.size()*2;
                newTable.resize(newSize);
                for(size_t i = 0; i < _table.size(); ++i) {
                    Node* cur = _table[i];
                    while(cur) {
                        Node* next = cur->_next;
                        size_t hashAddress = convert(cur->_kv.first) % newTable.size();
                        cur->_next = newTable[hashAddress];
                        newTable[hashAddress] = cur;
                        cur = next;
                    }
                    _table[i] = nullptr;
//                    if(_table[i]) {
//                        Node* cur = _table[i];
//                        Node* next = cur->_next;
//                        while(cur) {
//                            size_t hashAddress = convert(cur->_kv.first) % newTable.size();
//                            cur->_next = newTable[hashAddress];
//                            newTable[hashAddress] = cur;
//                            cur = next;
//                            if(cur)
//                                next = cur->_next;
//                        }
//                        // 也没必要其实
//                        _table[i] = nullptr;
//                    }
                }
                _table.swap(newTable);
            }
            // 通过哈希函数求哈希地址
            size_t hashAddress = convert(kv.first) % _table.size();
            Node* ptr = _table[hashAddress];
            Node* newNode = new Node(kv);
            // 每个哈希桶中进行头插
            newNode->_next = ptr;
            _table[hashAddress] = newNode;
            ++_size;
            return true;
        }

        Node* Find(const K& key) {
            if(_table.size() == 0) {
                return nullptr;
            }
            HDC convert;
            size_t hashAddress = convert(key) % _table.size();
            Node* cur = _table[hashAddress];
            while(cur) {
                if(cur->_kv.first == key) {
                    return cur;
                }
                cur = cur->_next;
            }
            return nullptr;
        }

        bool Erase(const K& key) {
            if(_table.size() == 0)
                return false;
            HDC convert;
            size_t hashAddress = convert(key) % _table.size();
            Node* cur = _table[hashAddress];
            Node* prev = nullptr;
            while(cur) {
                if(cur->_kv.first == key) {
                    if(prev)
                        prev->_next = cur->_next;
                    else
                        _table[hashAddress] = cur->_next;
                    delete cur;
                    --_size;
                    return true;
                }
                prev = cur;
                cur = cur->_next;
            }
            // 不存在该节点
            return false;
        }

        // 哈希表的长度
        size_t TableSize() {
            return _table.size();
        }

        // 非空哈希桶的个数
        size_t BucketNum() {
            size_t num = 0;
            for(auto&ptr:_table) {
                if(ptr)
                    num++;
            }
            return num;
        }

        // 哈希表中数据的个数
        size_t Size() {
            return _size;
        }

        // 最大的桶的长度
        size_t MaxBucketLength() {
            size_t max = 0;
            for(size_t i = 0; i < _table.size(); ++i) {
                size_t len = 0;
                Node* ptr = _table[i];
                while(ptr)
                {
                    len++;
                    ptr = ptr->_next;
                }
                if(len > max)
                    max = len;
//                if (len > 0)
//                    printf("[%d]号桶长度:%d\n", i, len);
            }
            return max;
        }
    private:
        vector<HashNode<K, V>*> _table;
        size_t _size = 0;
    };
}

开散列的负载因子和扩容问题：

注意：哈希表是需要扩容的，而是否扩容的衡量指标就是负载因子。

开散列中，当负载因子为1时，也就是理想情况下每个哈希桶中只挂一个元素时，进行扩容。因为再继续插入元素时，每一次都会发生哈希冲突，而开散列哈希表中若一个桶中的元素个数比较多时，会影响哈希表的性能。理想情况就是每个哈希桶中只挂一个元素，此时搜索时间复杂度为O(1)。

开散列和闭散列的比较：

应用链地址法处理哈希冲突，需要增设链接指针，似乎增加了存储开销。事实上： 由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <= 0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/13525.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MDF和DHF、DMR、DHR三者差异？注册与备案文件？

MDF和DHF、DMR、DHR三者差异？注册与备案文件？

医疗器械研发、工艺、注册、质量人员时常会接触到DHF, DMR, DHR。这几个单词缩写不光是拼写非常相似&#xff0c;其含义也有许多相同之处&#xff0c;所以十分容易混淆。本文就来聊一聊这三者的区别和联系。 ISO13485:2016 证明符合法规要求 MDF-Medical Device File&#xf…
阅读更多...
计算机毕业设计——税务缴纳信息管理

计算机毕业设计——税务缴纳信息管理

一.项目介绍 本项目包含管理员、普通用户两种角色 普通用户 可以浏览 首页、新闻信息、法律法规、税务政策、通知公告、留言板、个人中心、后台管理、在线咨询 普通用户进入后台管理可以修改密码、个人信息以及税务申报、填写留言 管理员用户登录可以操作 个人中心、用…
阅读更多...
服务器证书是网络信息安全的基础

服务器证书是网络信息安全的基础

我们都清楚&#xff0c;互联网安全存在两大基本隐患&#xff0c;一是因为身份认证机制的缺位&#xff0c;使网络成为各种“钓鱼”诈骗行为的温床&#xff0c;导致互联网空间缺乏信任。互联网每时每刻都在传输数以亿万的信息&#xff0c;这些信息如果未经加密&#xff0c;就有可…
阅读更多...
自动化测试如何区分用例集合及编写规范

自动化测试如何区分用例集合及编写规范

目录 前言 业务量和复杂度增长现状是什么&#xff1f; 如何区分自动化测试的用例集合&#xff1f; 区分用例集合的过程要注意什么&#xff1f; 自动化测试用例选择 自动化测试用例编写 用例编写规范 结语 前言 前面的文章介绍过如何设计自动化测试case&#xff0c;有同…
阅读更多...
一、翻越前端的三座大山——继承/原型链

一、翻越前端的三座大山——继承/原型链

文章目录原型专题前言什么是原型&#xff1f;实例和原型的关系什么是原型链&#xff1f;Object 和 Function 的继承关系原型运用例子&#xff1a;手写instanceof手写call&#xff0c;apply手写new六大继承方式原型链继承构造函数继承原型链 构造函数优化&#xff08;原型链 构…
阅读更多...
mysql 中的锁

mysql 中的锁

文章目录锁的分类锁粒度InnoDB 中的表锁InnoDB 中的行锁锁的分类 共享锁&#xff08;Shared Locks&#xff09; // 行共享锁 // 获取到当前记录的S锁&#xff08;共享锁&#xff09;&#xff0c;兼容其他事务的S锁&#xff0c;不兼容X锁&#xff08;排他锁&#xff09; select…
阅读更多...
服务注册中心

服务注册中心

什么是注册中心&#xff1f; 注册中心主要有三种角色&#xff1a; ● 服务提供者&#xff08;Provider&#xff09;&#xff1a;在启动时&#xff0c;向 Registry 注册自身服务&#xff0c;并向 Registry 定期发送心跳汇报存活状态。 ● 服务消费者&#xff08;Consumer&#…
阅读更多...
HCSC: Hierarchical Contrastive Selective Coding

HCSC: Hierarchical Contrastive Selective Coding

原型对比学习&#xff1a;图像表征与聚类中心之间的交互&#xff0c;可以简单总结为在表征空间中最大化图像特征与其所属的聚类中心的相似度。分层语义结构 自然存在于图像数据集中&#xff0c;其中几个语义相关的图像簇可以进一步集成到一个更大的簇中&#xff0c;具有更粗粒度…
阅读更多...
Tomcat多实例部署

Tomcat多实例部署

文章目录一、Tomcat多实例的操作步骤1、关闭防火墙&#xff0c;将安装 Tomcat 所需软件包传到/opt目录下2、安装JDK3、安装 tomcat4、配置 tomcat 环境变量5、修改 tomcat2 中的 server.xml 文件&#xff0c;要求各 tomcat 实例配置不能有重复的端口号6、修改各 tomcat 实例中的…
阅读更多...
openpnp软件的使用 - 配置自动电动飞达

openpnp软件的使用 - 配置自动电动飞达

文章目录openpnp软件的使用 - 配置自动电动飞达概述笔记新建执行器(电动飞达类型)新建电动飞达的料站配置飞达的x,y位置配置飞达移动到料表面时的高度测试这个Z高度, 是否能让吸嘴取得元件?设置元件料封装使用的吸嘴.试试开始贴片贴片后的元件位置目测备注ENDopenpnp软件的使用…
阅读更多...
实操小微风控报告中的地址信息的清洗与照面和司法数据使用

实操小微风控报告中的地址信息的清洗与照面和司法数据使用

在中小微企业的大数据风控体系中&#xff0c;工商数据与司法数据是最基本也是最常见的两类信息维度&#xff0c;在企业大数据体系的应用场景中扮演着重要角色。由于企业工商与司法数据的多部分内容属于社会公开化信息&#xff0c;因此在行业市场内也是非常容易获取的&#xff0…
阅读更多...
详解：看似遥不可及的元宇宙

详解：看似遥不可及的元宇宙

导语：元宇宙是人们娱乐、生活乃至工作的虚拟时空。Roblox 这款游戏，展示了元宇宙的诸多特征。核心是数字创造、数字资产、数字交易、数字货币和数字消费，尤其是在用户体验方面，达到了真假难辨、虚实混同的境界。 大约再过15 年，互联网就可能会发生一次重大的变革。正如从…
阅读更多...
技术 | 终端安全 | 服务器并不像您想象的那么安全

技术 | 终端安全 | 服务器并不像您想象的那么安全

在从1到10的评分中&#xff0c;现状方法对服务器安全的有效性如何&#xff1f; 从理论上讲&#xff0c;应该是10分。保护服务器免受外界影响的途径(分段、防火墙、漏洞修补、安全解决方案等)是众所周知的。 然而&#xff0c;现实生活的结果显示出与理论的巨大差距。从红十字会…
阅读更多...
【前端】Ajax-form表单与模板引擎

【前端】Ajax-form表单与模板引擎

目录 一、form表单的基本使用 1.1什么是表单 1.2表单的组成部分 1.3form标签属性 1.4表单的同步提交及缺点 1.4.1什么是表单的同步提交 1.4.2表单同步提交的缺点 1.4.3如何解决表单同步提交的缺点 二、通过Ajax提交表单数据 2.1监听表单提交事件 2.2阻止表单默认提交…
阅读更多...
（超级详细1秒钟秒懂）华为网络初级工程师知识总结（一）

（超级详细1秒钟秒懂）华为网络初级工程师知识总结（一）

文章目录一&#xff0c;人机交互的工作模式二&#xff0c;OSI参考模型---OSI/RM三&#xff0c;常见的网络协议端口号四&#xff0c;网络层的地址查询&#xff0c;转发。五&#xff0c;ARP协议的转发原理六&#xff0c;TCP/IP协议的封装和解封装及跨层封装一&#xff0c;人机交互…
阅读更多...
预编码ZF,MMSE,THP准则线性预编码误码率仿真

预编码ZF,MMSE,THP准则线性预编码误码率仿真

目录 1.算法概述 2.仿真效果预览 3.核心MATLAB代码预览 4.完整MATLAB程序 1.算法概述 恒定包络( Constant Enve-lope&#xff0c;CE) 预编码&#xff1b; 该算法规定&#xff0c;每根天线上的发射功率被限定为一个与信道条件和信号符号均无关的常数&#xff0c;各根天线均…
阅读更多...
Nacos下载和安装步骤

Nacos下载和安装步骤

1. 下载安装包 1.1. Nacos官网 :https://nacos.io/zh-cn/hub 打开官网&#xff0c;点击前往Github 1. Nacos官网 1.2. 打开Nacos Github主页&#xff0c;点击Release&#xff0c;点击tags&#xff0c;可以看到所有的版本&#xff0c;选择自己需要的版本下载 Nacos Github主页 …
阅读更多...
线性代数 --- 投影Projection 四（投影有什么用？Why projection）

线性代数 --- 投影Projection 四（投影有什么用？Why projection）

笔者在本系列的开篇就说过&#xff0c;我在学习投影的过程中&#xff0c;有很长的一段时间都是把重点放在了&#xff0c;如何计算投影本身&#xff0c;也就是背公式。 现在我发现&#xff08;尤其是明白了投影即分量之后&#xff09;&#xff0c;学习投影的主要目的&#xff0c…
阅读更多...
IB数学AA/AI应该如何选择？IB数学AA HL有多难？

IB数学AA/AI应该如何选择？IB数学AA HL有多难？

IB课程即国际文凭组织IBO&#xff0c;是为全球学生开设从幼儿园到大学预科的课程&#xff0c;为3-19岁的学生提供智力、情感、个人发展、社会技能等方面的教育&#xff0c;使其获得学习&#xff0c;工作以及生存于世的各项能力。 IB课程难在哪&#xff1f; IB课程不像AP、A-lev…
阅读更多...
读书笔记-学习GNU Emacs-1

读书笔记-学习GNU Emacs-1

学习本书目的&#xff1a; emacs的学习一直是陆陆续续看博客和上手实践&#xff0c;这次想通过阅读"学习GNU Emacs"这本书好好系统的再复习下emacs。 ps:读技术书应该是带着一定的目的去读的&#xff0c;最简单的目的可能就是为了学好某一项技术或者复习下某一项技术…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023