一、一元二次方程

1、定义

只含有一个未知数，且未知数的最高次数是2的整式方程。
表达式：ax²+bx+c=0

2、常用解法

1、直接开平方法
2、配方法
3、公式法。(常用)
x=[-b±√(b-4ac)]/2a

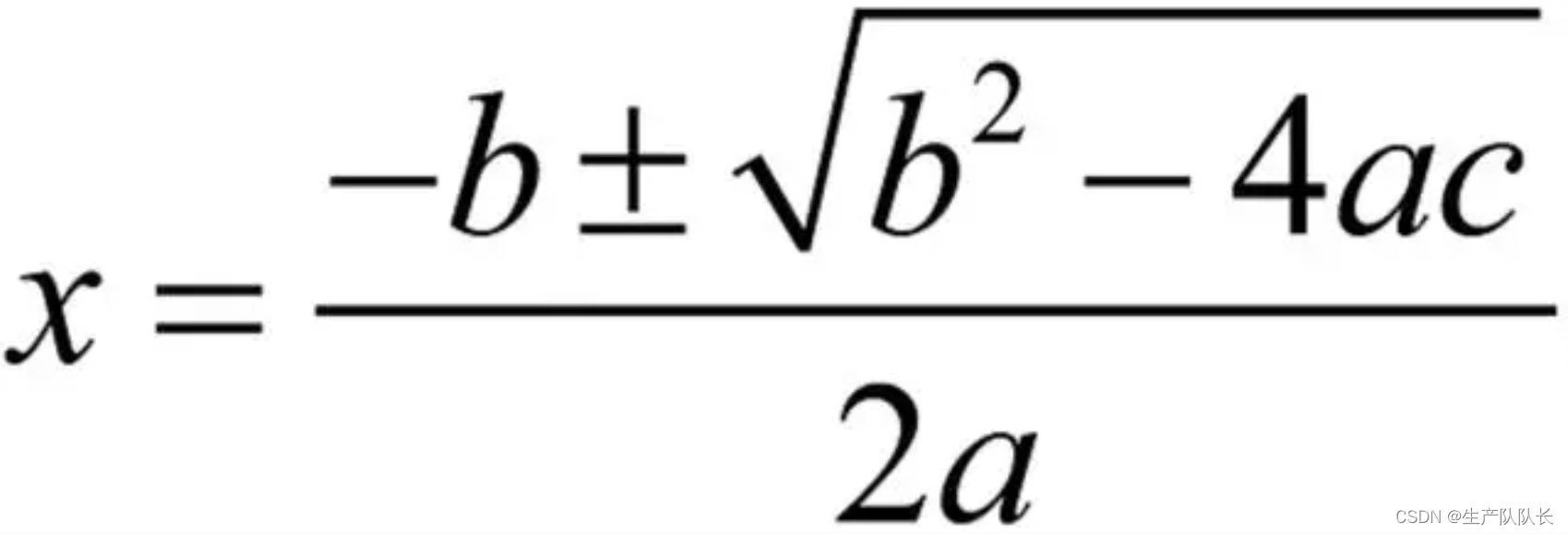
4、因式分解法（十字相乘法）(常用)
将方程通过因式分解变形为：(x-m)*(x-n)=0的形式，则两个根就是m和n。

3、判别式

∆=b^2-4ac
∆>0,有两个不等实数根
∆=0,有两个相等实数根
∆<0,没有实数根（无解）

4、根于系数的关系

如果ax²+bx+c=0方程的两个实数根是m和n
则：m+n=-b/a；m*n=c/a

二、一元二次函数

1、图像

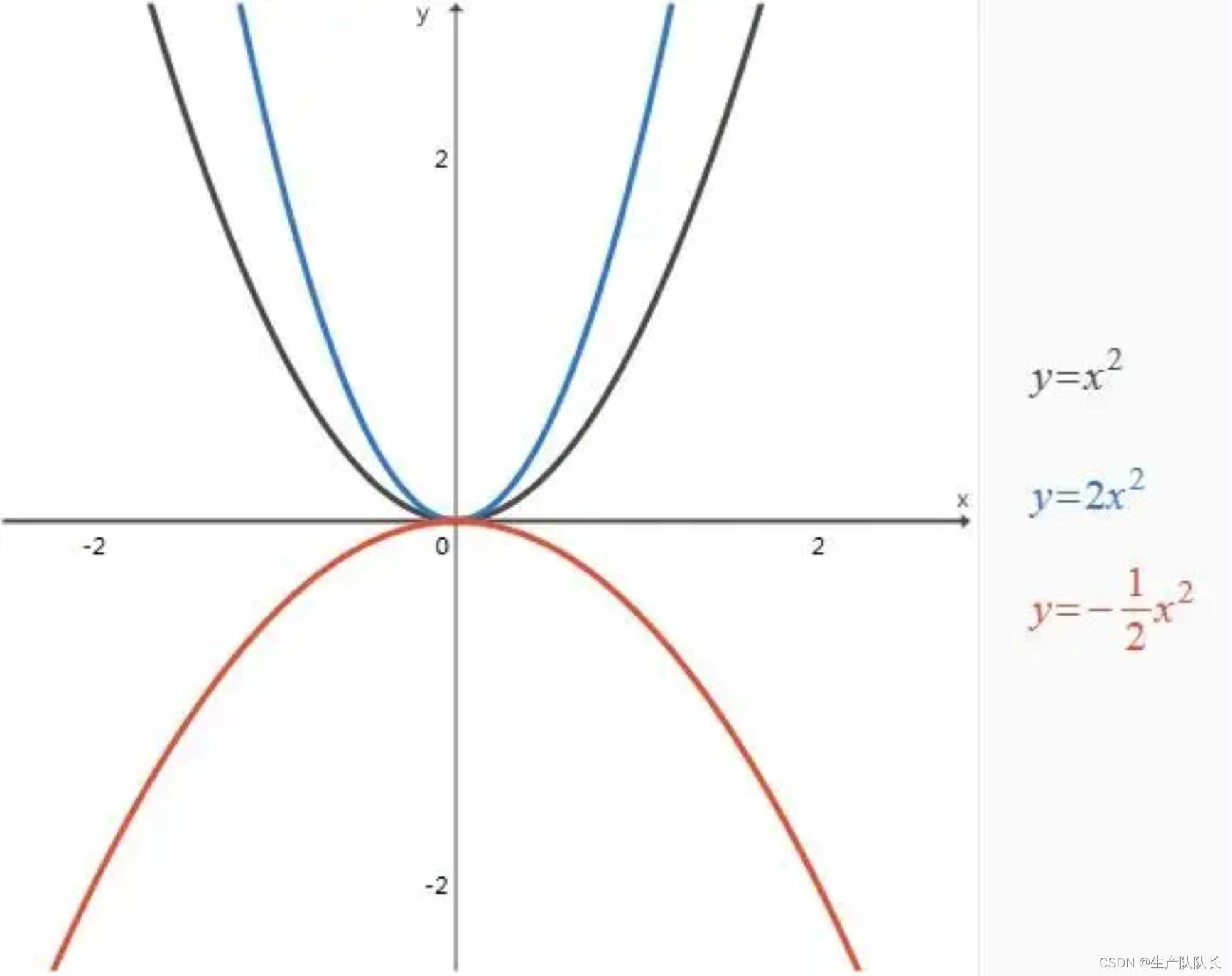
2、解析式

1、一般式
2、顶点式

3、两根式

3、一般常用性质了解

（1）a>0时，抛物线开口向上（与y轴正向一致）。
（2）a<0时，抛物线开口向下（与y轴负向一致）。
（3）|a|越大，抛物线开口越小。
（4）|a|越小，抛物线开口越大。

对称轴：-b/2a