一、介绍

        DEEP学习在人工智能领域迈出了一大步。目前，神经网络在非表格数据（图像、视频、音频等）上的表现优于其他类型的算法。深度学习模型通常具有很强的复杂性，并提出数百万甚至数十亿个可训练的参数。这就是为什么在现代使用加速技术来减少训练时间至关重要的原因。

        在训练过程中执行的最常见算法之一是反向传播，包括神经网络相对于给定损失函数的权重变化。反向传播通常通过梯度下降来执行，梯度下降试图逐步将损耗函数收敛到局部最小值。

        事实证明，朴素梯度下降通常不是训练深度网络的首选，因为它的收敛速度很慢。这成为研究人员开发加速梯度下降的优化算法的动力。

在阅读本文之前，强烈建议您熟悉优化算法中使用的指数移动平均线概念。如果没有，您可以参考下面的文章。

二、梯度下降

        梯度下降是最简单的优化算法，它计算相对于模型权重的损失函数梯度，并使用以下公式更新它们：

        梯度下降方程。w 是权重向量，dw 是 w 的梯度，α 是学习率，t 是迭代次数

        为了理解为什么梯度下降会缓慢收敛，让我们看一下下面的峡谷示例，其中两个变量的给定函数应该最小化。

        沟壑区域梯度下降的优化问题示例。起点以蓝色表示，局部最小值以黑色表示。

沟壑是表面在一个维度上比在另一个维度上陡峭得多的区域

        从图像中，我们可以看到起点和局部最小值具有不同的水平坐标，并且几乎是相等的垂直坐标。使用梯度下降来求局部最小值可能会使损失函数向垂直轴缓慢振荡。发生这些反弹是因为梯度下降不存储有关其先前梯度的任何历史记录，从而使梯度步骤在每次迭代时更加不确定。此示例可以推广到更多的维度。

因此，使用较大的学习率是有风险的，因为它可能导致收敛。

三、动量

        基于上面的例子，希望使损失函数在水平方向上执行较大的步长，在垂直方向上执行较小的步长。这样，收敛速度会快得多。这种效果正是由 Momentum 实现的。

        Momentum 在每次迭代时都使用一对方程式：

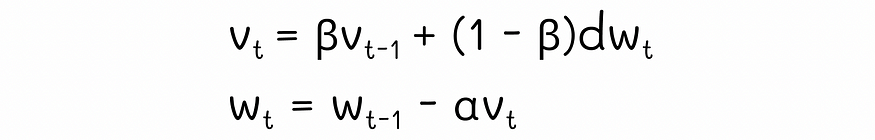
        动量方程

        第一个公式对梯度值 dw 使用指数移动平均值。基本上，这样做是为了存储有关一组先前梯度值的趋势信息。第二个方程使用当前迭代中计算出的移动平均值执行正常梯度下降更新。α是算法的学习率。

        动量对于上述情况特别有用。想象一下，我们在每次迭代中都计算了梯度，如上图所示。我们不是简单地使用它们来更新权重，而是取几个过去的值，并在平均方向上执行字面上的更新。

塞巴斯蒂安·鲁德（Sebastian Ruder）在他的论文中简明扼要地描述了动量的影响：“对于梯度指向相同方向的维度，动量项会增加，而对于梯度改变方向的维度，动量项会减少更新。因此，我们获得了更快的收敛速度并减少了振荡。

因此，Momentum 执行的更新可能如下图所示。

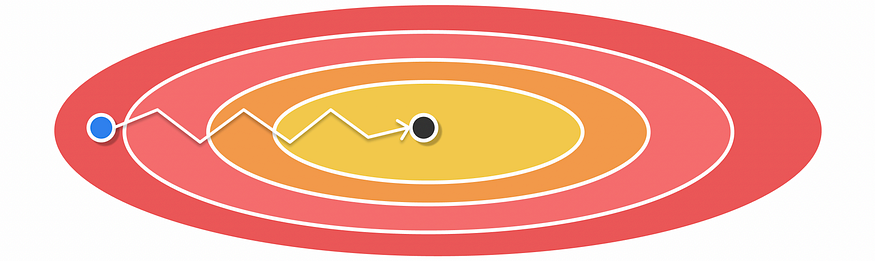
利用 Momentum 进行优化

在实践中，动量收敛速度通常比梯度下降快得多。借助 Momentum，使用更高的学习率的风险也更小，从而加快了训练过程。

在 Momentum 中，建议选择接近 0.9 β。

四、AdaGrad（自适应梯度算法）

        AdaGrad 是另一个优化器，其动机是根据计算出的梯度值调整学习率。在训练过程中，可能会出现这样的情况：权重向量的一个分量具有非常大的梯度值，而另一个分量的梯度值非常小。当不频繁的模型参数似乎对预测的影响很小时，尤其会发生这种情况。值得注意的是，对于频繁的参数，此类问题通常不会发生，因为对于它们的更新，模型使用了大量的预测信号。由于梯度计算会考虑来自信号的大量信息，因此梯度通常足够，并且表示朝向局部最小值的正确方向。然而，对于罕见的参数来说，情况并非如此，这会导致极大且不稳定的梯度。对于稀疏数据，如果有关某些要素的信息太少，则也会出现同样的问题。

        AdaGrad 通过独立调整每个权重成分的学习率来解决上述问题。如果对应于某个权重向量分量的梯度很大，则相应的学习率将很小。相反，对于较小的梯度，学习率会更大。这样，Adagrad 就可以处理梯度消失和爆炸问题。

        在引擎盖下，Adagrad 从所有先前迭代中累积了元素平方 dw² 的梯度。在权重更新期间，AdaGrad 不使用正常的学习率α，而是通过将α除以累积梯度 √vt） 的平方根来对其进行缩放。此外，在分母上添加了一个小的正项ε，以防止潜在的除以零。

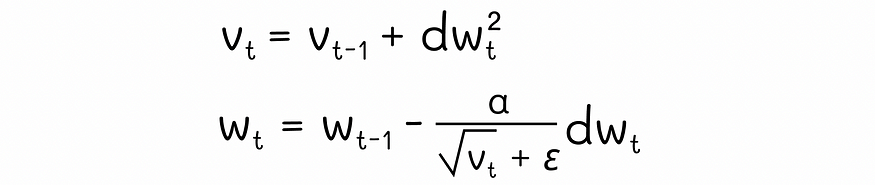
AdaGrad 方程

        AdaGrad 的最大优点是不再需要手动调整学习率，因为它会在训练过程中自行调整。然而，AdaGrad 也有不利的一面：学习率随着迭代次数的增加而不断衰减（学习率总是除以正累积数）。因此，算法在最后一次迭代期间趋向于缓慢收敛，此时收敛变得非常低。

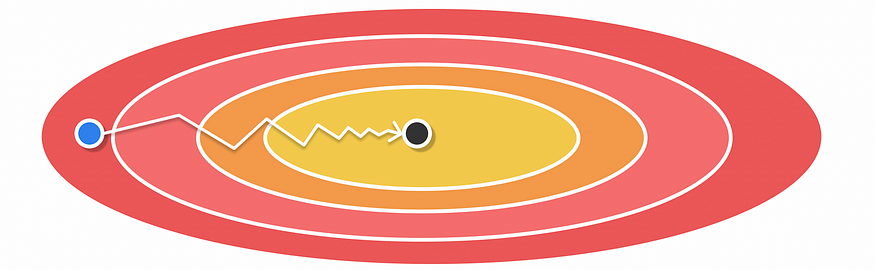
使用 AdaGrad 进行优化

五、RMSProp（均方根传播）

        RMSProp 被详细阐述为对 AdaGrad 的改进，解决了学习率衰减的问题。与 AdaGrad 类似，RMSProp 使用一对权重更新完全相同的方程。

RMSProp 方程

        但是，不是存储 vt 的梯度 dw² 的平方和，而是计算梯度 dw² 的平方移动平均值。实验表明，RMSProp 通常比 AdaGrad 收敛得更快，因为在指数移动平均值中，它更强调最近的梯度值，而不是通过简单地从第一次迭代中累积梯度来平均分配所有梯度的重要性。此外，与 AdaGrad 相比，RMSProp 中的学习率并不总是随着迭代次数的增加而衰减，从而可以在特定情况下更好地适应。

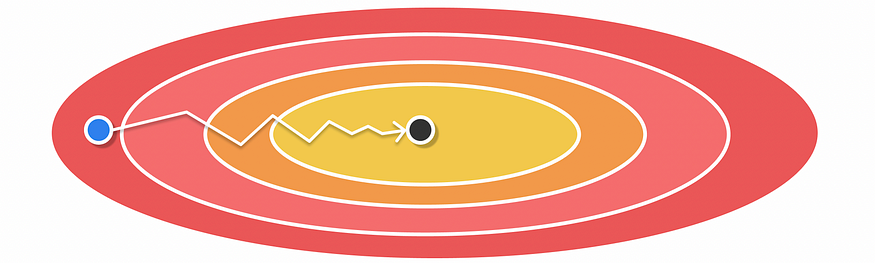
使用 RMSProp 进行优化

在 RMSProp 中，建议选择接近 1 β。

为什么不简单地使用v t的平方梯度而不是指数移动平均线呢？

众所周知，指数移动平均线将较高的权重分配给最近的梯度值。这是 RMSProp 快速适应的原因之一。但是，如果我们只考虑每次迭代时的最后一个平方梯度 （vt = dw²），而不是移动平均线，那不是更好吗？事实证明，更新方程将按以下方式转换：

使用平方梯度而不是指数移动平均线时 RMSProp 方程的变换

正如我们所看到的，得到的公式看起来与梯度下降中使用的公式非常相似。但是，我们现在没有使用正常的梯度值进行更新，而是使用梯度符号：

• 如果 dw > 0，则权重 w 减少 α。
• 如果 dw < 0，则权重 w 增加 α。

综上所述，如果 vt = dw²，则模型权重只能按 ±α 更改。虽然这种方法有时有效，但它仍然不灵活，算法对α的选择变得非常敏感，并且梯度的绝对幅度被忽略，这可能使该方法的收敛速度非常慢。该算法的一个积极方面是，只需要一个位来存储 gradietns 的迹象，这在具有严格内存要求的分布式计算中非常方便。

六、亚当（自适应矩估计）

        目前，Adam是深度学习中最著名的优化算法。在高层次上，Adam 结合了 Momentum 和 RMSProp 算法。为了实现它，它只是分别跟踪计算梯度和平方梯度的指数移动平均值。

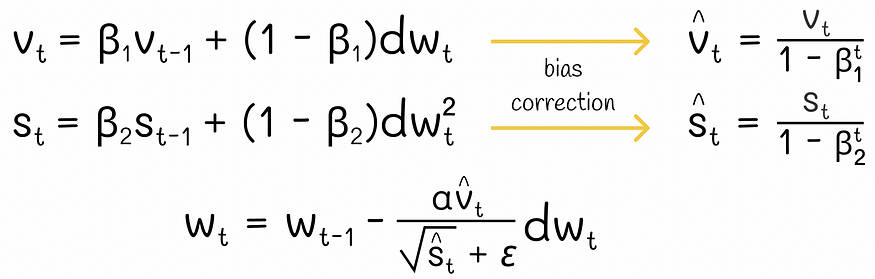
亚当方程

        此外，还可以对移动平均线使用偏差校正，以便在前几次迭代中更精确地近似梯度趋势。实验表明，Adam 利用 Momentum 和 RMSProp 的优势，很好地适应了几乎任何类型的神经网络架构。

与Adam一起优化

根据 Adam 论文，超参数的良好默认值为 β₁ = 0.9，β₂ = 0.999，ε = 1e-8。

七、结论

        我们已经研究了神经网络中不同的优化算法。作为 Momentum 和 RMSProp 的组合，Adam 是其中最优越的一个，它能够稳健地适应大型数据集和深度网络。此外，它具有简单的实现和很少的内存要求，使其成为大多数情况下的首选。

资源

• 梯度下降优化算法概述
• Adam：一种随机优化方法

 图片作者提供