1、 模型评估
那我们如何测量预测函数 fθ(x)的正确性,也就是精度呢?
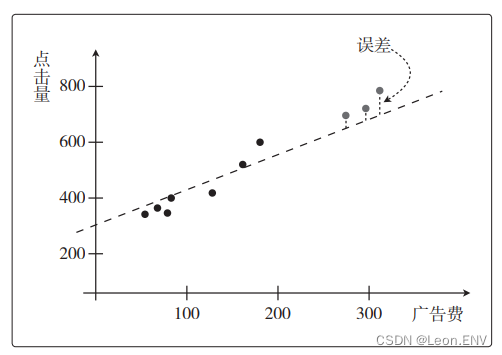
观察函数的图形,看它能否很好地拟合训练数据:
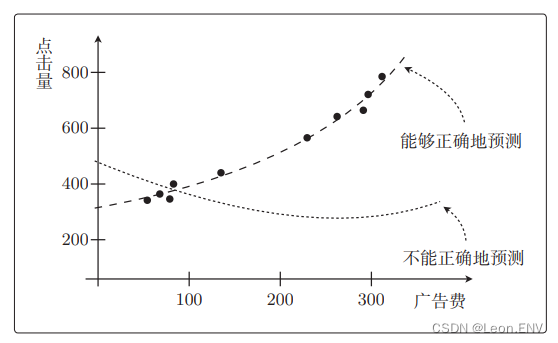
这是只有一个变量的简单问题,所以才能在图上展 示出来。
过像多重回归这样的问题,变量增加后就不能在图上展示了。
所以我们需要能够定量地表示机器学习模型的精度。
2、 交叉验证
回归问题的验证
把获取的全部训练数据分成两份:一份用于测试,一份用于训练,然后用前者来评估模型。
如果变量增加,就不能画图了,就算能画图,也会很麻烦。
对于回归的情况,只要在训练好的模型上计算测试数据的误差的平方,再取其平均值就可以了。假设测试数据有 n 个,那么可以 这样计算:
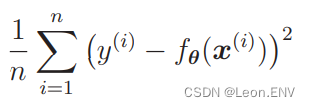
这个值被称为均方误差或者
MSE,全称 Mean Square Error。
这个误差越小,精度就越高,模型也就越好。
分类问题的验证
由于回归是连续值,所以可以从误差入手, 但是在分类中我们必须要考虑分类的类别是否正确。
我们是根据图像为横向的概率来分类的, 关于分类是否成功就会有下面 4 种情况:

设横向的情况为正、非横向的情况为负,那么一般来 说,二分类的结果可以用这张表来表示:
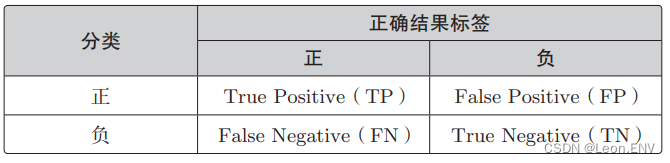
分类结果为正的情况是 Positive、为负的情况是 Negative。分类 成功为 True、分类失败为 False。
我们可以使用表里的 4 个记号来计算分类的精度。精 度的英文是 Accuracy,它的计算表达式是这样的:

它表示的是在整个数据集中,被正确分类的数据 TP 和 TN 所占 的比例。
假如 100 个数据中 80 个被正确地分类了,那么精度就是这样:

精确率和召回率
一般来说,只要计算出这个 Accuracy 值,基本上就可以掌握分类 结果整体的精度了。
但是有时候只看这个结果会有问题,所以还 有别的指标。
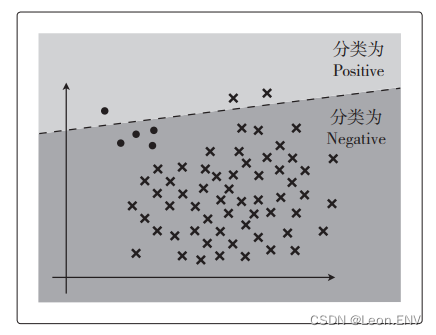
假设图中的圆点是 Positive 数据、叉号是 Negative 数据,我们来考虑一下数据量极其不平衡的情况:

假设有 100 个数据,其中 95 个是 Negative。那么,哪怕出现模型把数据全部分类为 Negative 的极端情况,Accuracy 值也为 0.95, 也就是说模型的精度是 95%。
但是不管精度多高,一个把所有数据都分类为 Negative 的模型, 不能说它是好模型。
假设分类如下:
首先我们来看第一个指标——
精确率。它的英文是 Precision:

这个指标只关注 TP 和 FP。根据表达式来看,它的含义是在被分类为 Positive 的数据中,实际就是 Positive 的数据所占的比例:

(这个值越高,说明分类错误越少。)
还有一个指标是
召回率,英文是 Recall:

这个指标只关注 TP 和 FN。根据表达式来看,它的含义是在 Positive 数据中,实际被分类为 Positive 的数据所占的比例:
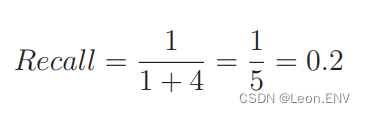
(
这个值越高,说明被正确分类的数据越多。
)
基于这两个指标来考虑精度是比较好的,不过一般来说,精确率和召回率会一个高一个低,需要我们取舍,有些麻烦。
F 值
假设现在有两个模型, 它们的精确率和召回率是这样的:

如果将所有的数据都分类为 Positive,那么召回率就是 1.0。但是 这样一来,Negative 数据也会被分类为 Positive,所以精确率会变得很低。
看一下两个模型的平均值,会发现模型 B 的更高。但它是把所有 数据都分类为 Positive 的模型,精确率极低,仅为 0.02,并不能说它是好模型。
所以就出现了评定综合性能的指标 F 值。表达式中的 Fmeasure 就是 F 值,Precision 是前面说的精确率,Recall 是召回率:

精确率和召回率只要有一个低,就会拉低 F 值。计算一下前面两个模型的 F 值就知道了:
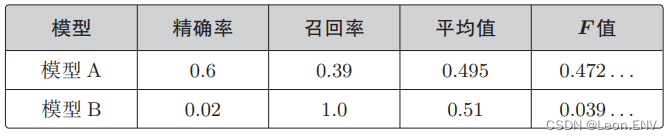
这说明该指标考虑到了精确率和召回率的平衡。其实,也有很多人把前面那个 F 值的表达式变形,写成下面这样,二者是相同的:

有时称 F 值为 F1 值会更准确,这一点需要注意。
F 和 F1 有的时候含义相同,有的时候却并不相同。
除 F1 值之外,还有一 个带权重的 F 值指标:

我们可以认为
F 值指的是带权重的 F 值,当权重为 1 时才 是刚才介绍的 F1 值。
F1 值在数学上是精确率和召回率的调和平均值。关于调和平均值,不需要太深入地了解。
之前介绍的精确率和召回率都是以 TP 为主进行计 算的,那么也能以 TN 为主:

以哪个为主都可以吗?
当数据不平衡时,使用数量少的那个会更好。最开始的例子中 Positive 极少,所以我们使用了 Positive 来计算,反之如果 Negative 较少,那就使用 Negative。
对于回归和分类,我们都可以这样来评估模型。
把全部训练数据分为测试数据和训练数据的做法称为交叉验证,这是非常重要的方法。
交叉验证的方法中,尤为有名的是
K 折交叉验证,掌握这种方法很有好处:
● 把全部训练数据分为 K 份
● 将 K − 1 份数据用作训练数据,剩下的 1 份用作测试数据
● 每次更换训练数据和测试数据,重复进行 K 次交叉验证
● 最后计算 K 个精度的平均值,把它作为最终的精度
假如我们要进行 4 折交叉验证,那么就会这样测量精度:
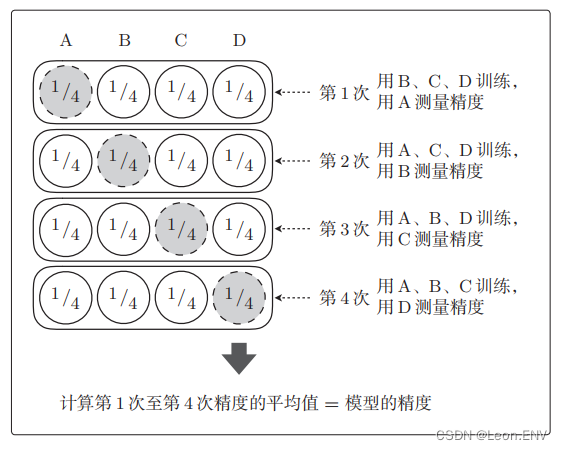
如果全部训练数据的量较大,这种方法必须训练多次,会比较花时间。
不切实际地增加 K 值会非常耗费时间,所以我们必须要确定一个合适的 K 值。
3、正则化
过拟合
之前我们提到过的模型只能拟合训练数据的状态被称为过拟合, 英文是 overfitting。
如: 过度增加函数 fθ(x)的次数会导致过拟合。
有几种方法可以避免过拟合:
● 增加全部训练数据的数量
● 使用简单的模型
● 正则化
首先,重要的是增加全部训练数据的数量。机器 学习是从数据中学习的,所以数据最重要。
另外,
使用更简单的模型也有助于防止过拟合。
正则化的方法
在讲解回归的时候提到的目标函数:
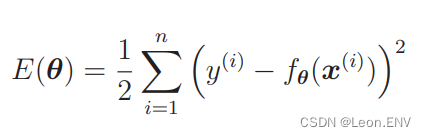
我们要向这个目标函数增加下面这样的正则化项:
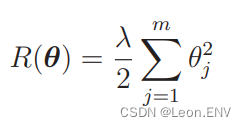
得到新的目标函数:

我们要对这个新的目标函数进行最小化,这种方法就称为 正则化。
不过一般来说不对 θ0 应用正则化,所以仔细看会发现 j 的 取值是从 1 开始的。
这也就是说,假如预测函数的表达式为 fθ(x) = θ0 + θ1x + θ2x^2 , 那么 m = 2 就意味着正则化的对象参数为 θ1 和 θ2。
θ0 这种只有参数的项称为偏置项,一般不对它进行正则化。
λ 是决定正则化项影响程度的正的常数,这个值需要我们自己来定。
正则化的效果
首先把目标函数分成两个部分:

所以我们实际地 把这两个函数的图形画出来,加起来看看。
把这两个函数的图形画出来,加起来看看。
不过参数太多就画不出图来了,所以这里我们只关注 θ1。而且为了更加易懂,先不考 虑 λ。
不用太在意形状是否精确, 假设它的形状是这样的:
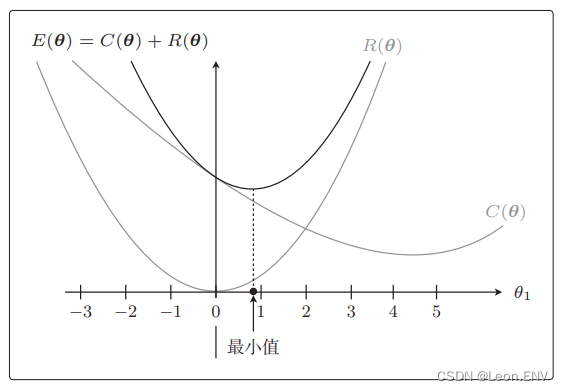
C(θ) :θ1 = 4.5 附近是最小值。
E(θ) = C(θ) + R(θ): θ1 = 0.9 附近是最小值。
与加正则化项之前相比,θ1 更接近 0 了。
这就是正则化的效果。它可以防止参数变得过大,有助于参数接近较小的值。
虽然我们只考虑了 θ1,但其他 θj 参数的情况也是类似的。
参数的值变小,意味着该参数的影响也会相应地变小。比如,有这样的一个预测函数 fθ(x):

再极端一点,假设 θ2 = 0,这个表达式就从二次变为一次了:

这就意味着本来是曲线的预测函数变为直线了。
这正是通过减小不需要的参数的影响,将复杂模型替换为简单模型来防止过拟合的方式。
不过刚才的只是个例子,并不是一定要减小次数最高项的参数值。
就是为了防止参数的影响过大,在训练时要对参数施加一些惩罚。
那一开始就提到的 λ,是可以控制正则化惩罚的强度:
比如令 λ = 0,那就相当于不使用正则化。
反过来 λ 越大,正则化的惩罚也就越严厉:

分类的正则化
刚才讨论的是回归的情况,对于分类也可以应用正则化。
逻辑回归的目标函数:
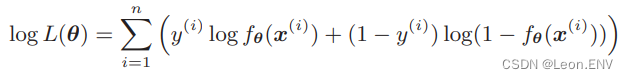
分类也是在这个目标函数中增加正则化项就行了, 道理是相同的:
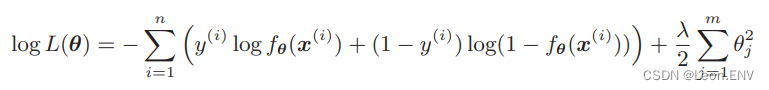
为什么在原来的目标函数上加上负号?
对数似然函数本来以最大化为目标。但是,这次我想让它变成和回归的目标函数一样的最小化问题,所以加了负号。这样就可以 像处理回归一样处理它,所以只要加上正则化项就可以了。
反转符号是为了将最大化问题替换为最小化问题。
反转了符号之后,在更新参数时就要像回归一样,与微分的函数的符号反方向移动才行。
包含正则化项的表达式的微分
目标函数分成了 C(θ) 和 R(θ):
因为是加法,所以对各部分进行偏微分:
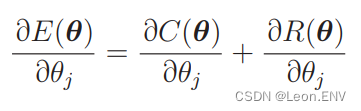
C(θ) 是原来的目标函数,讲解回归的时候我们已经求过它 的微分形式了:

所以接下来只要对正则化项进行微分就行了:
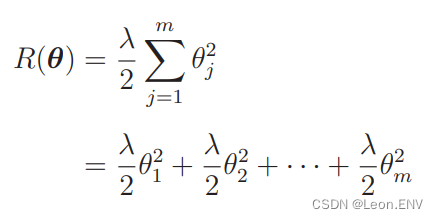
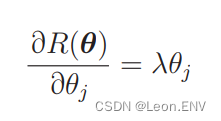
最终的微分结果就是这样:
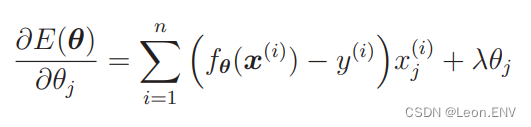
剩下要做的就是把这个微分结果代入到参数更新表达式里去:

不过,我们之 前说过一般不对 θ0 应用正则化。R(θ) 对 θ0 微分的结果为 0,所 以 j = 0 时表达式的 λθj 就消失了。因此,实际上我们需 要像这样区分两种情况:

逻辑回归的流程也是一样的:
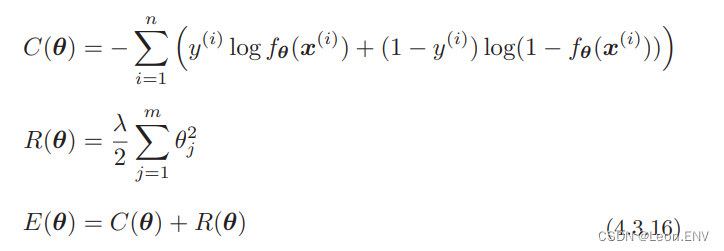
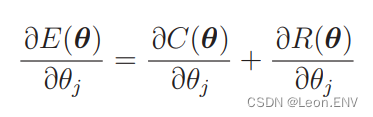
不过现在考虑的是最小化问题,所以要注意在前面加上负号:

最后得到:
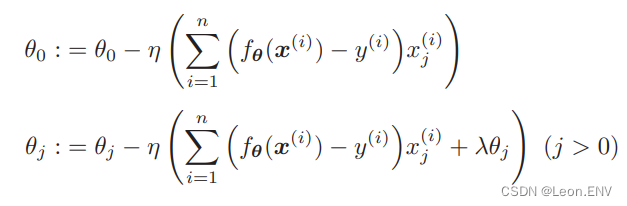
刚才介绍的方法其实叫
L2 正则化。
除 L2 正则化方法之外,还有
L1 正则化方法,它的正则化项 R 是这样的:
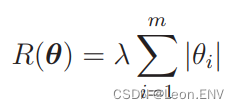
L1 正则化的特征是被判定为不需要的参数会变为 0,从而减少变 量个数。
L2 正则化不会把参数变为 0。
刚才说过二次式变为 一次式的例子,用 L1 正则化就真的可以实现了。
L2 正则化会抑制参数,使变量的影响不会过大,而 L1 会直接去除不要的变量。
使用哪个正则化取决于要解决什么问题,不能一概而论。
4、学习曲线
欠拟合
前面我们聊了很多过拟合的话题,而反过来又有一种叫作欠拟合的状态,用英文说是 underfitting。在这种情况下模型的性能也会变差。
欠拟合是与过拟合相反的状态,所以它是没有拟合训练数据的状态。
比如用直线对图中这种拥有复杂边界线的数据进行分类的情况,无论怎样做都不能很好地分类,最终的精度会很差:
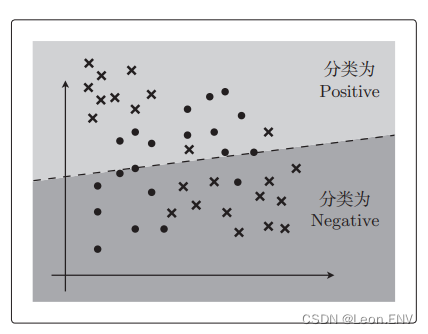
出现这种情况的主要原因就是模型相对于要解决的问题来说太简单了。
过拟合与欠拟合基本上是相反关系,原因不同,解决方案 也不同。
区分过拟合与欠拟合
只根据精度不能判断是哪种不好的拟合。
我们以数据的数量为横轴、以精度为纵轴,然后把用于训练的数据和用于测试的数据画成图来看一看就知道了:

这里我想说的就是如果模型过于简单,那么随着数据量的增加,误差也会一点点变大。换句话说就是精度会一点点下降。
用测试数据先评估根据 2 个训练数据训练好的模型,再评估根据 10 个训练数据训练好的模型,然后依次求出精度。
训练数据较少时训练好的模型难以预测未知的数据,所以精度很低;
反过来说,训练数据变多时,预测精度就会一点点地变高。
用图来展示就是这样的:

将两份数据的精度用图来展示后,如果是这种形状,就说明出现 了欠拟合的状态。
也有一种说法叫作
高偏差,指的是一回事。
这是一种即使增加数据的数量,无论是使用训练数据还是测试数据,精度也都会很差的状态。
图中需要注意的点在这里:
该图为欠拟合:

而在过拟合的情况下,图是这样的,这也叫作
高方差:
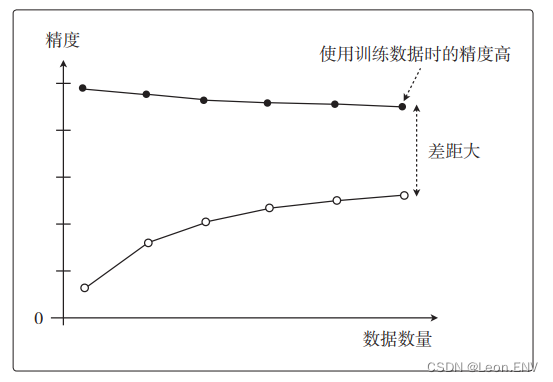
随着数据量的增加,使用训练数据时的精度一直很高,而使用测试数据时的精度一直没有上升到它的水准。 只对训练数据拟合得较好,这就是过拟合的特征。
像这样展示了数据数量和精度的图称为学习曲线。
通过学习曲线判断出是过拟合还是欠拟合之后,就可以采 取相应的对策以便改进模型了。