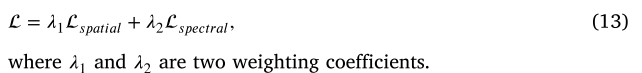git 如何撤销历史某次merge

news2025/1/12 20:58:58

git，如何撤销某一次历史提交或merge，并保留该版本的后续提交？

场景1：

你有两个功能迭代版本的分支，一个是 15 号上线，一个是25号上线。5号的时候产品突然说，这两个版本一起上，然后你耿直的把25号版本merge到了15号版本。

几天后产品说：“一起上有问题，我们还是分开上吧”。这个时候你发现merge之后又提交了很多15号版本的代码，需要撤销那次merge并且保留后面的提交。

场景2：

所有人共用 test 分支，有五个人都在这上面合并了自己的代码，结果有天 A 不小心把 develop 分支合并到了 test，过了一会 A 发现，并且想撤回的时候，发现再次期间，有好几个人都提交了代码。所以不能用reset，而是需要撤销merge并且保留后面更改。

git revert

git revert -m 1 commitId

Git 之 revert

revert 可以取消指定的某次提交内容。

当讨论 revert 时，需要分两种情况，因为 commit 分为两种：一种是常规的 commit，也就是使用 git commit 提交的 commit；另一种是 merge commit，在使用 git merge 合并两个分支之后，你将会得到一个新的 merge commit。

merge commit 和普通 commit 的不同之处在于 merge commit 包含两个 parent commit，代表该 merge commit 是从哪两个 commit 合并过来的。

在上图所示的红框中有一个 merge commit，使用 git show 命令可以查看 commit 的详细信息

➜  git show bd86846
commit bd868465569400a6b9408050643e5949e8f2b8f5
Merge: ba25a9d 1c7036f

这代表该 merge commit 是从 ba25a9d 和 1c7036f 两个 commit 合并过来的。

而常规的 commit 则没有 Merge 行

➜  git show 3e853bd
commit 3e853bdcb2d8ce45be87d4f902c0ff6ad00f240a

revert 常规 commit

使用 git revert <commit id> 即可，git 会生成一个新的 commit，将指定的 commit 内容从当前分支上撤除。

revert merge commit

revert merge commit 有一些不同，这时需要添加 -m 选项以代表这次 revert 的是一个 merge commit

但如果直接使用 git revert ，git 也不知道到底要撤除哪一条分支上的内容，这时需要指定一个 parent number 标识出"主线"，主线的内容将会保留，而另一条分支的内容将被 revert。

如上面的例子中，从 git show 命令的结果中可以看到，merge commit 的 parent 分别为 ba25a9d 和 1c7036f，其中 ba25a9d 代表 master 分支（从图中可以看出），1c7036f 代表 will-be-revert 分支。需要注意的是 -m 选项接收的参数是一个数字，数字取值为 1 和 2，也就是 Merge 行里面列出来的第一个还是第二个。

我们要 revert will-be-revert 分支上的内容，即保留主分支，应该设置主分支为主线，操作如下：

➜ git revert -m 1 bd86846

revert 之后重新上线

假设狗蛋在自己分支 goudan/a-cool-feature 上开发了一个功能，并合并到了 master 上，之后 master 上又提交了一个修改 h，这时提交历史如下：

a -> b -> c -> f -- g -> h (master)
           \      /
            d -> e   (goudan/a-cool-feature)

突然，大家发现狗蛋的分支存在严重的 bug，需要 revert 掉，于是大家把 g 这个 merge commit revert 掉了，记为 G，如下：

a -> b -> c -> f -- g -> h -> G (master)
           \      /
            d -> e   (goudan/a-cool-feature)

然后狗蛋回到自己的分支进行 bugfix，修好之后想重新合并到 master，直觉上只需要再 merge 到 master 即可（或者使用 cherry-pick），像这样：

a -> b -> c -> f -- g -> h -> G -> i (master)
           \      /               /
            d -> e -> j -> k ----    (goudan/a-cool-feature)

i 是新的 merge commit。但需要注意的是，这不能得到我们期望的结果。因为 d 和 e 两个提交曾经被丢弃过，如此合并到 master 的代码，并不会重新包含 d 和 e 两个提交的内容，相当于只有 goudan/a-cool-feature 上的新 commit 被合并了进来，而 goudan/a-cool-feature 分支之前的内容，依然是被 revert 掉了。

所以，如果想恢复整个 goudan/a-cool-feature 所做的修改，应该先把 G revert 掉：

a -> b -> c -> f -- g -> h -> G -> G' -> i (master)
           \      /                     /
            d -> e -> j -> k ----------    (goudan/a-cool-feature)