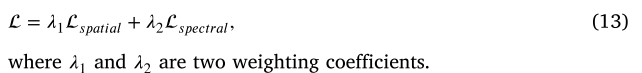文章目录
- 1. 这篇论文做了什么事,有什么贡献?
- 2. Related Work
- 铰接物体建模
- 3D中的Diffusion model扩散模型
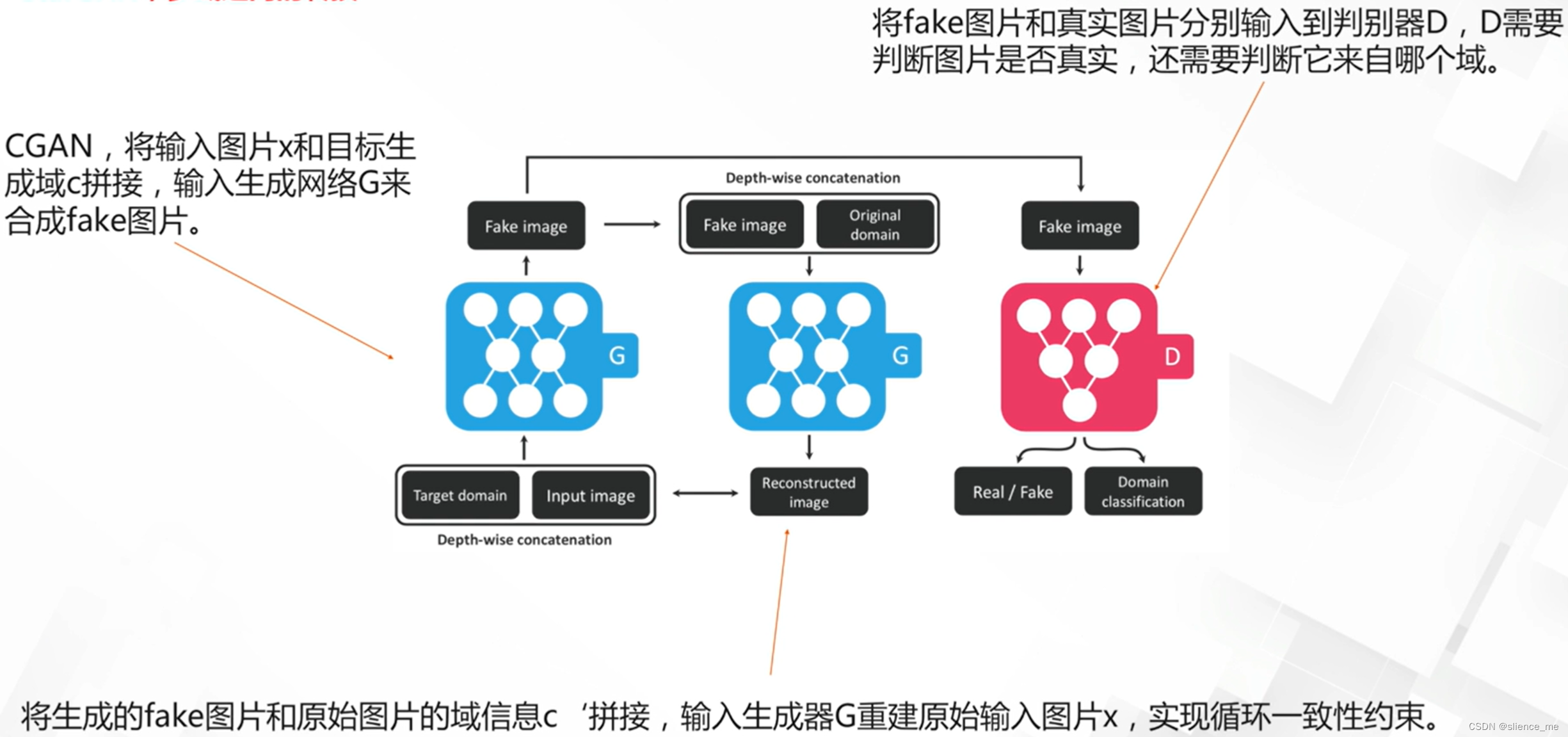
- 3. Pipeline
- 铰接树参数化
- 基于Diffusion的铰接树生成
- 去噪网络
- 4. 实验
- 评价铰接物体生成——以往做法与本文提出的新指标
- NAP捕捉到的铰接物体分布质量
- NAP是否足够高效?——消融实验
- NAP可以做一些什么应用?
- 5. 总结
- 6. 其他补充
- SE(3) transformation
- Positional Encoding位置编码
1. 这篇论文做了什么事,有什么贡献?
本篇论文研究铰接物体的生成模型。目前已经有大量工作研究3D物体的生成、组合的生成、场景的生成,但是对于人类和机器人日常交互对象——铰接物体的生成则很少有人focus。
生成铰接物体不仅包括生成几何的分布和位置(铰接物体是由rigid part组成的,要生成这些几何分布及其所在的位置),还需要生成两个rigid part之间的相对运动(比如运动结构,铰接链等信息)。
困难(Challenge)在于:现有的铰接物体数据集中存在的铰接物体,存在着许多不同,如他们在rigid part的数量(比如门是两个rigid part,然后眼镜这些是三个rigid part)上不同,且存在着多样化的连接拓扑(不同铰接物体连接的方式可能有差异)和不同的关节运动类型(有prismatic,如抽屉那种,还有revolute,门和眼镜那种)
为了解决这些困难和挑战,本文做出了以下的贡献:
- 针对于铰接物体之间存在的如rigid part数量不同、连接拓扑和关节运动类型不同等这种种差异,论文提出了一种统一的parameterization方式来表示铰接物体,论文称这种表达方式为铰接树
- 在这种参数化后的物体上,运用最近比较火的diffusion去噪概率模型来建模铰接物体的不规则分布
- 通过一个图注意力机制去噪网络,来逐步交换这种参数化后的铰接物体图之间的边与节点之间的信息
- 引入了一个新的度量指标来评估这个新的任务
2. Related Work
铰接物体建模
这方面的工作主要分成几个部分:铰接物体类别估计、铰接物体重建、铰接物体模拟、铰接物体生成。
类别估计方面的工作主要是从传感器观察中预测铰接关节状态(铰接角度和)和铰接参数(铰接类型、axis的位置和朝向信息、限制),使用的方法主要是概率模型、交互感知的方式、基于学习的推理。
重建方面就是重建物体的铰接属性和几何属性,使用的技术主要包括运动、基于学习的方法和隐式神经表示。这些方法主要是做表面重建,关节状态预测
本文主要是建立一个铰接物体的生成先验
3D中的Diffusion model扩散模型
作者聚焦于那些3D shape和运动的生成。
Shape:目前Diffusion models在生成点云、mesh、隐式表面、nerf和4D非网格shape上做的很好。但是Diffusion models生成shape的工作主要是focus在单一物体的level上,没有focus在具有运动结构的物体上。
Motion:最近有很多在铰接物体运动生成方面的运用。类似的工作还有基于text生成人体运动、音频驱动、场景感知、多人或动画领域等。Diffusion models for motion还被运用于策略规划,视觉电机控制,重新排列任务等。这些将Diffusion model运用在运动方面的工作大部分都基于已知的几何和已知的运动结构。我们与之不同,我们共同建模几何和运动结构先验来建立铰接物体。
3. Pipeline
铰接树参数化
要想使用diffusion model来进行铰接物体的处理,首先就应该将铰接物体以某种方式实现参数化。首先引入铰接树参数化法,这也是本文的一个contribution:每一个物体都被定义成一个图,并同时做出两个假设:
- 树assumption:假设图是一个无环连接图(每两个节点间最多只有一条边连接),且能够通过边走完整个图
- Screw关节:假设边是连接用的螺丝,最多只具有prismatic平移和revolute旋转中的一种性质,以此覆盖了大部分真实世界中的铰接物体

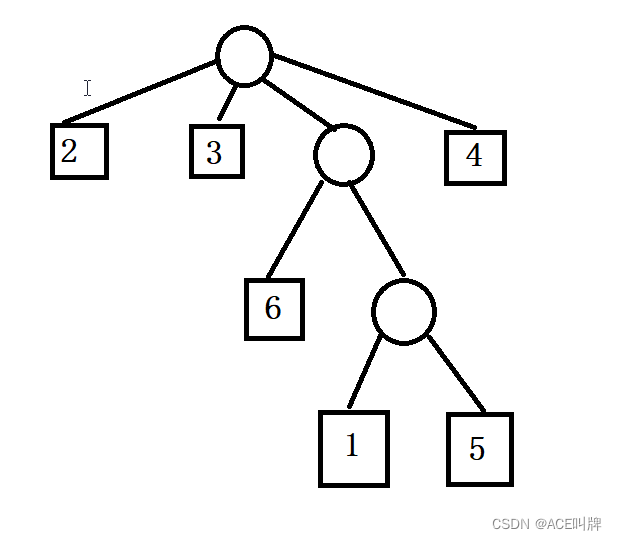
Node
如图所示,每一个rigid part在图中都会被表示为一个Node,每一个joint都有其初始的pose,对应于0°或者未展开的状态。
给定其中第
i
i
i个part,首先获得从局部坐标
y
i
y_i
yi经过SE(3)变换得到的全局坐标
y
g
=
T
g
i
y
i
y_g=T_{gi}y_i
yg=Tgiyi,
T
g
i
∈
R
6
T_{gi}∈R^6
Tgi∈R6
每一个part的几何通过一个bounding box
b
i
∈
R
3
b_i∈R^3
bi∈R3进行表示,以及适配于bounding box大小的一个神经隐式表面
预训练了一个occupancy shape autoencoder,将每个part shape转换成一个latent code
s
i
∈
R
F
s_i∈R^F
si∈RF
最后,为了建模结构有差异的多种物体,这里最多允许表示具有K个parts的物体,并使用二进制占用符
o
i
∈
{
0
,
1
}
o_i∈\{0,1\}
oi∈{0,1}来表示每个part是否存在
故综合以上内容,Node被表示为 v i = [ o i , T g i , b i , f i ] ∈ R D v v_i=[o_i,T_{gi},b_i,f_i]∈R^{D_v} vi=[oi,Tgi,bi,fi]∈RDv,且 D v = 1 + 6 + 3 + F D_v=1+6+3+F Dv=1+6+3+F,因为最多可以表示K个parts的物体,所以这部分的维度就是 K × D v K×D_v K×Dv
Edges
根据Chasles的理论,SE(3) transformation可以表示为沿着轴的2D旋转和1D平移,且可以通过单位Plücker坐标来定义这样一个轴。这里使用具有单位方向
l
l
l和垂直于
l
l
l的动量
m
m
m的Plücker坐标来统一表示prismatic和revolute joints(
l
∈
S
2
,
m
∈
R
3
l∈S^2, m∈R^3
l∈S2,m∈R3)。在全局坐标系下定义Plücker坐标
p
(
i
,
j
)
p_{(i,j)}
p(i,j),以避免两个parts的父子顺序发生翻转时引起的局部坐标变化。
我理解这里所谓的
l
∈
S
2
l∈S^2
l∈S2,应该指的是方位角和俯仰角,通过方位角和俯仰角来定义单位球面上的一个方向向量,然后
m
m
m表示的是轴的旋转或平移动量(虽然我还不太理解这一点)
为了完整地定义关节运动,还使用
r
(
i
,
j
)
∈
R
2
×
2
r_{(i,j)}∈R^{2×2}
r(i,j)∈R2×2来表示关节的运动范围。如果关节是一个纯粹的prismatic关节,其旋转的范围就会被定义为
[
0
,
0
]
[0,0]
[0,0],反之亦然。两个part之间的相对变换使用
T
(
θ
,
d
)
T(θ,d)
T(θ,d)来表示,实际上这里
θ
θ
θ就是一个旋转角度,然后
d
d
d是一个移动范围。通过
T
(
θ
,
d
)
T(θ,d)
T(θ,d)和全局坐标
(
l
g
,
m
g
)
(l_g,m_g)
(lg,mg)计算局部坐标:
(
l
i
,
m
i
)
=
(
R
i
g
l
g
,
R
i
g
m
g
+
t
i
g
×
(
R
i
g
l
g
)
)
(l_i,m_i)=(R_{ig}l_g,R_{ig}m_g+t_{ig}×(R_{ig}l_g))
(li,mi)=(Riglg,Rigmg+tig×(Riglg))
接着根据局部坐标计算旋转和平移:
R
=
R
(
θ
,
l
i
)
,
t
=
(
I
−
R
(
θ
,
l
i
)
)
(
l
i
×
m
i
)
+
d
l
i
R=R(θ,l_i),t=(I-R(θ,l_i))(l_i×m_i)+dl_i
R=R(θ,li),t=(I−R(θ,li))(li×mi)+dli
同时,还定义一个手性指示符 c i , j ∈ { − 1 , 0 , + 1 } c_{i,j}∈\{-1,0,+1\} ci,j∈{−1,0,+1},0表示边不存在,+1和-1表示的手性(我认为就是表示的父子关系,parent-child)。
综合以上内容,Edge被表示为
e
(
i
,
j
)
=
[
c
i
,
j
,
p
(
i
,
j
)
,
r
(
i
,
j
)
]
∈
R
D
e
e_{(i,j)}=[c_{i,j}, p_{(i,j)}, r_{(i,j)}]∈R^{D_e}
e(i,j)=[ci,j,p(i,j),r(i,j)]∈RDe,且
D
e
=
1
+
6
+
4
D_e=1+6+4
De=1+6+4,因为最多有K个Node,所以无向边的数量最多是
K
(
K
−
1
)
/
2
K(K-1)/2
K(K−1)/2,所以这部分的维度就是
K
(
K
−
1
)
/
2
×
D
e
K(K-1)/2×D_e
K(K−1)/2×De。
这种图的表示最终会使用最小生成树来进行后处理,每个图都对应一棵唯一的树,也就是唯一的articulated object。
基于Diffusion的铰接树生成
正向过程

正向就和传统的Diffusion一样是一个简单的扩散过程。首先定义完整的铰接图
x
=
(
v
i
,
e
(
i
,
j
)
)
∈
R
K
D
v
+
K
(
K
−
1
)
D
e
/
2
x=({v_i},{e_{(i,j)}})∈R^{KD_v+K(K-1)D_e/2}
x=(vi,e(i,j))∈RKDv+K(K−1)De/2。
从物体的分布
q
(
x
0
)
q(x_0)
q(x0)中采样了铰接图
x
0
x_0
x0,逐渐在
x
0
x_0
x0上加上随时间变化的噪声
β
1
−
β
T
β_1-β_T
β1−βT,进而获得了
x
1
−
x
T
x_1-x_T
x1−xT,最终
x
T
x_T
xT是以高斯分布为结尾的
p
(
x
T
)
=
N
(
x
T
;
0
,
I
)
p(x_T)=N(x_T;0,I)
p(xT)=N(xT;0,I),这个过程可以被如下表示:
q
(
x
1
:
T
∣
x
0
)
:
=
∏
t
=
1
T
q
(
x
t
∣
x
t
−
1
)
,
q
(
x
t
∣
x
t
−
1
)
:
=
N
(
1
−
β
t
x
t
−
1
,
β
t
I
)
q(x_{1:T}|x_0):=\prod_{t=1}^{T}q(x_t|x_{t-1}),q(x_{t}|x_{t-1}):=N(\sqrt{1-β_t}x_{t-1},β_tI)
q(x1:T∣x0):=t=1∏Tq(xt∣xt−1),q(xt∣xt−1):=N(1−βtxt−1,βtI)
由于Diffusion自身特有的特性,我们也可以直接从
x
0
x_0
x0来表示
x
t
x_t
xt:
q
(
x
t
∣
x
0
)
:
=
N
(
α
‾
t
x
0
,
(
1
−
α
‾
t
)
I
)
,
α
t
:
=
1
−
β
t
,
α
‾
t
:
=
∏
s
=
1
t
α
s
q(x_{t}|x_{0}):=N(\sqrt{\overline{α}_t}x_{0},(1-\overline{α}_t)I),α_t:=1-β_t,\overline{α}_t:=\prod^t_{s=1}α_s
q(xt∣x0):=N(αtx0,(1−αt)I),αt:=1−βt,αt:=s=1∏tαs
逆向过程
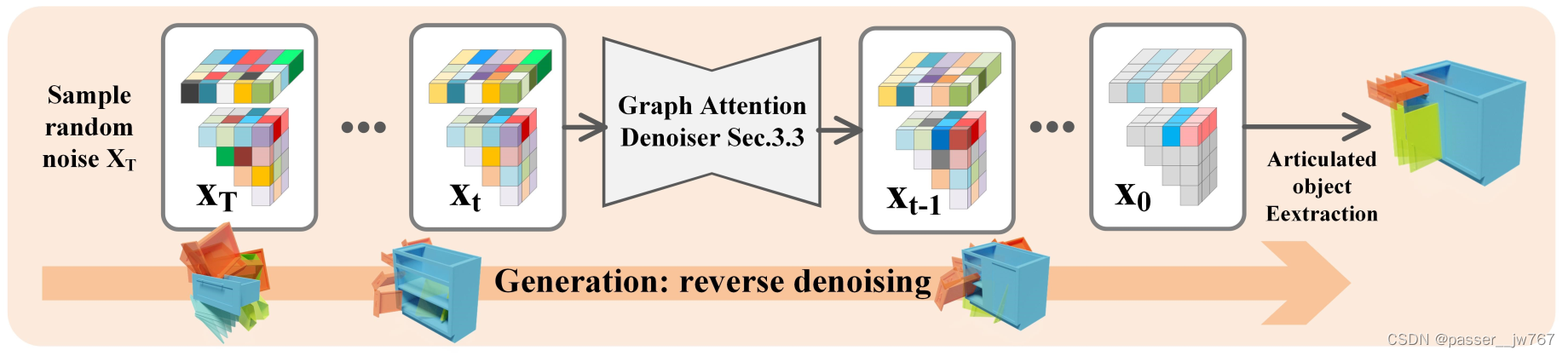
逆向过程从标准的高斯分布开始,通过一个带有可学习参数
θ
θ
θ的神经网络来学习如何移除噪声,逆向过程表示为:
p
(
x
0
:
T
)
:
=
p
(
x
T
)
∏
t
=
1
T
p
θ
(
x
t
−
1
∣
x
t
)
,
p
θ
(
x
t
−
1
∣
x
t
)
:
=
N
(
μ
θ
(
x
t
,
t
)
,
∑
θ
(
x
t
,
t
)
)
p(x_{0:T}):=p(x_T)\prod_{t=1}^{T}p_θ(x_{t-1}|x_t),p_θ(x_{t-1}|x_{t}):=N(μ_θ(x_t,t),\sum_{θ}(x_t,t))
p(x0:T):=p(xT)t=1∏Tpθ(xt−1∣xt),pθ(xt−1∣xt):=N(μθ(xt,t),θ∑(xt,t))
Follow之前的工作,设定
∑
θ
(
x
t
,
t
)
=
σ
t
2
I
\sum_{θ}(x_t,t)=\sigma^2_tI
∑θ(xt,t)=σt2I,并根据Langevin dynamics来建模逆向过程(直观地理解来说,就是给定
x
t
x_t
xt及当前时间步t,通过网络来推断当前时间步下的噪声,
x
t
x_t
xt减去这个噪声后得到的就是未加上该步噪声的结果
x
t
−
1
x_{t-1}
xt−1):
x
t
−
1
=
1
α
t
(
x
t
−
1
−
α
t
1
−
α
‾
t
ϵ
θ
(
x
t
,
t
)
)
+
σ
t
z
,
z
来自正态分布
x_{t-1}=\frac{1}{\sqrt{α_t}}(x_t-\frac{1-α_t}{\sqrt{1-\overline{α}_t}}\epsilon_θ(x_t,t))+\sigma_tz,z来自正态分布
xt−1=αt1(xt−1−αt1−αtϵθ(xt,t))+σtz,z来自正态分布
ϵ
θ
(
x
t
,
t
)
\epsilon_θ(x_t,t)
ϵθ(xt,t)是通过不断优化每一步的的
x
t
x_t
xt来学习的网络参数
训练目标
总的来讲,Diffusion的训练目标就是使得正向和逆向的分布尽可能一致,通过使它们的负对数尽可能接近于0,使Forward和Reverse的两个分布尽量接近:
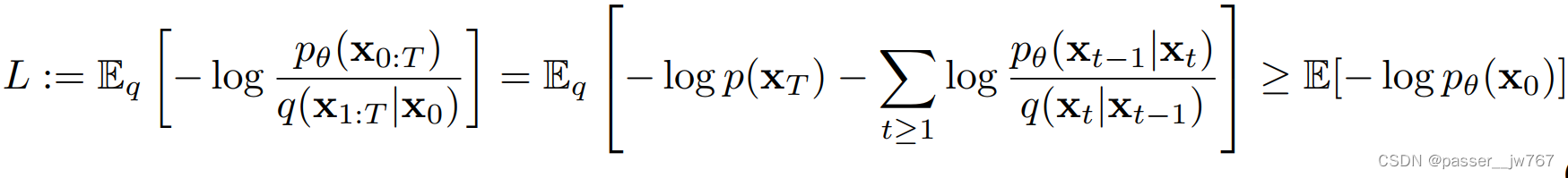
简化后的训练目标很简单,就是使得网络预测出来的噪声和加进去的噪声尽可能地一致:
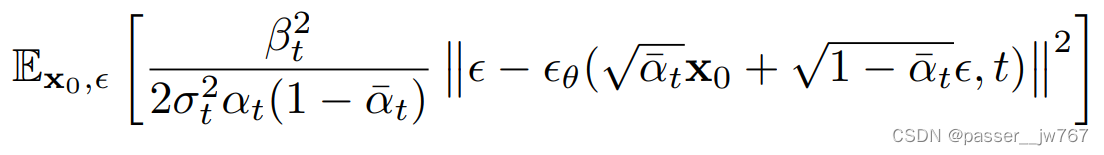
输出提取
在获得了输出的参数化结果后,通过后处理步骤来获得最终的铰接物体。大致过程如下:
首先,通过生成的节点指示符
o
o
o来定义存在的这些节点,同时需要确保最少有两个节点。
接着,根据预测的边的手性
∣
c
∣
|c|
∣c∣来找到生成图的最小生成树,得到树的拓扑。
最后,预测的joint坐标将会从
R
6
R^6
R6投影到Plücker坐标(
l
∈
S
2
,
m
∈
R
3
l∈S^2, m∈R^3
l∈S2,m∈R3)中。
每个part的shape code将会被通过一个decoder解码成SDF的形式,并通过marching cube获得对应的mesh。
有条件的生成
Diffusion model最讨喜的一个性质是如果想要做基于条件的diffusion,可以直接通过贝叶斯论将条件直接加入到推理过程中,而不需要对训练过程中做任何修改。这里的条件可以是part、joint等等
在这里,作者通过fix x x x已知的part执行条件生成,像图像重绘和形状补全一样,对于 x x x,通过mask将输入分为已知部分和未知部分: x = m ⊙ x k n o w + ( 1 − m ) ⊙ x u n k n o w x=m\odot x^{know}+(1-m)\odot x^{unknow} x=m⊙xknow+(1−m)⊙xunknow。对于已知部分的输入,可以直接从 q ( x 0 ) q(x_0) q(x0)中进行采样,通过给已知部分 x k n o w x^{know} xknow加上高斯噪声,就可以在反向过程中通过diffusion来补全未知部分 x u n k n o w n x^{unknown} xunknown
去噪网络
网络结构
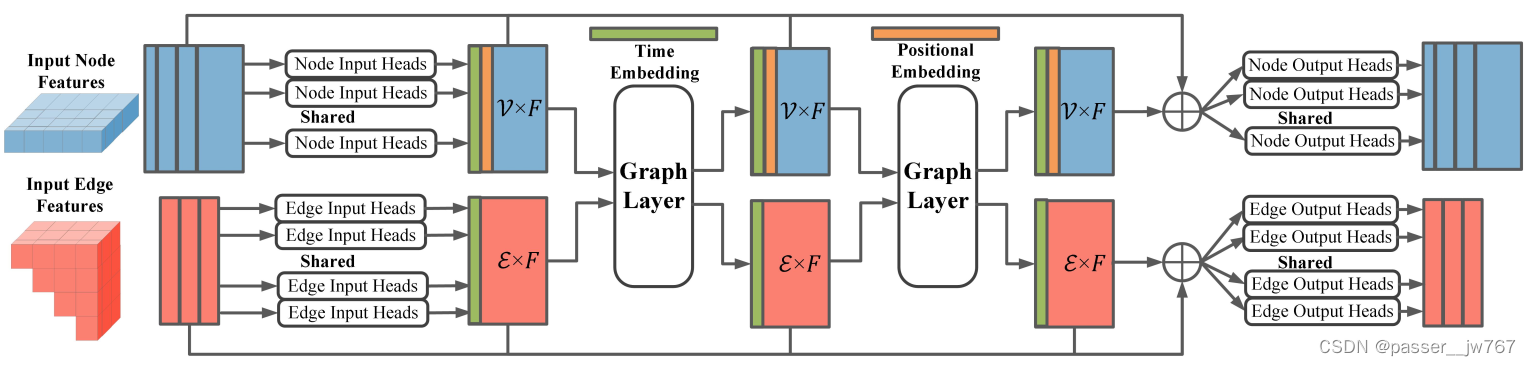
利用了一个图注意力机制来做去噪网络,网络的输入是带有噪声的铰接图
x
x
x,输出是和输入
x
x
x shape相同的噪声,网络结构中的权重,在去噪的全过程中都是权重共享的。
开始,分别将节点和边输入到各自的网络中获得Node features
{
f
i
}
\{f_i\}
{fi}和Edge features
{
g
(
i
,
j
)
}
\{g_{(i,j)}\}
{g(i,j)},
接着,这两组节点会被通过Graph layer进行更新,以实现特征之间的交换和融合
最后,所有的隐藏特征,包括输入的特征,当前时间步t,都将会被输出头进行解码
类似于近期的一些场景图生成工作,这里还会将部件实例id的位置编码(positional encoding)联合结点特征作为输入,以在早期部件的pose信息具有二义性的时候,提供更强的引导
Graph layer
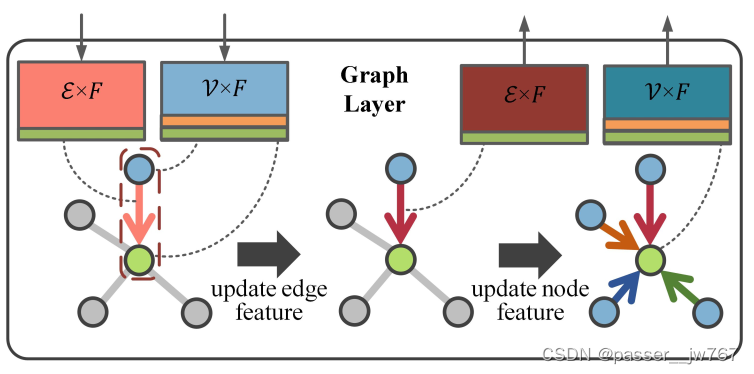
edge特征首先通过一个edge MLP,混合输入的edge特征
g
(
i
,
j
)
g_{(i,j)}
g(i,j)和相邻Node
i
,
j
i,j
i,j的特征进行更新:
g
(
i
,
j
)
′
=
M
L
P
(
f
i
,
f
j
,
g
(
i
,
j
)
)
g^{'}_{(i,j)}=MLP(f_i,f_j,g_{(i,j)})
g(i,j)′=MLP(fi,fj,g(i,j))
接着将更新后的edge特征通过注意力权重反向更新结点Node(这个权重可以衡量Edge对Node的影响)
这里的权重计算方法为:通过两个MLP从输入的Node中计算Query
Q
(
f
i
)
Q(f_i)
Q(fi)和Key
K
(
f
j
)
K(f_j)
K(fj),并使用二者的内积作为注意力权重,节点Node
i
i
i的权重计算方式为: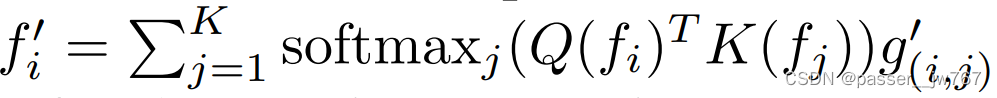
最后还使用了类似于PointNet中的全局池化来捕捉全局信息
4. 实验
在实验中阐述了4个问题,分别对应于实验的4个小节:
- 如何评估铰接物体生成?
- NAP捕捉到的铰接物体分布质量如何?
- NAP是否足够高效?
- NAP可以做一些什么应用?
评价铰接物体生成——以往做法与本文提出的新指标
以往做法中,评价铰接物体生成大部分是通过COV来评价生成样例的多样性,或者通过Jenson-Shannon divergence (JSD)来计算生成样例和参考样例之间的相似性等。
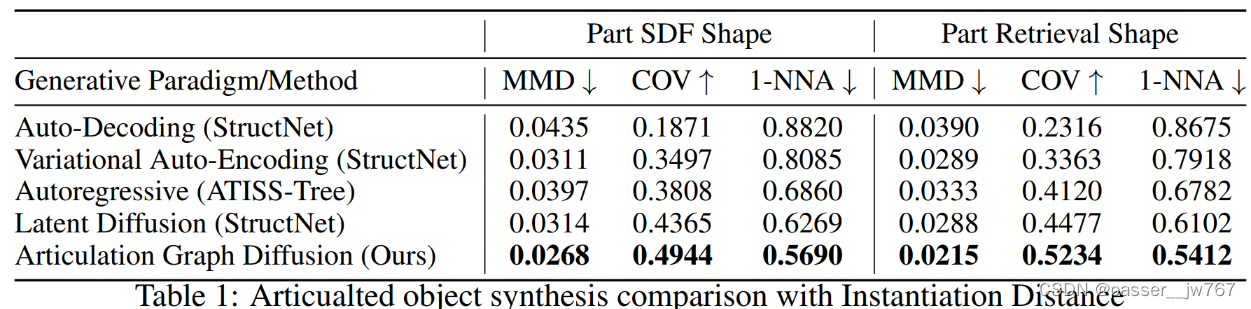
在这里本文提出了新的评价指标。作者说在现有的评价指标中,不分开对shape geometry和kinematic structure的评价,大部分多是fix geometry评价kinematic structure,或者反过来fix kinematic structure而评价geometry,对于一些图生成工作,只评价其结构而不评价其几何。这里就提出了一种新的距离指标——Instantiation Distance(ID)来测量两个铰接物体之间的距离,同时考虑了部件几何和运动结构。
将铰接物体
O
O
O作为一个模板,给定合理关节范围内的所有关节状态
q
∈
Q
O
q∈Q_O
q∈QO,将会得到一组铰接mesh
M
(
q
)
M(q)
M(q)和一组部件姿态
T
(
q
)
=
T
p
a
r
t
∈
S
E
(
3
)
T(q)={T_{part}∈SE(3)}
T(q)=Tpart∈SE(3),通过计算两个铰接物体不同关节状态下的距离通过:
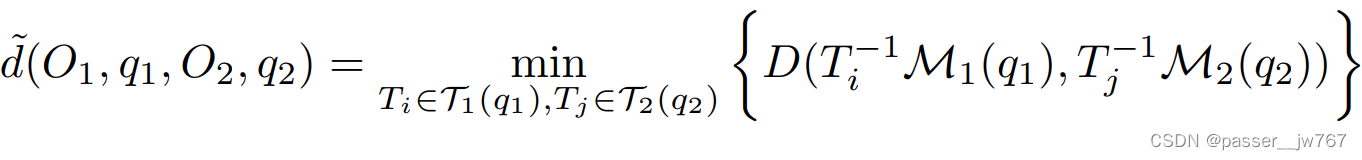
其中,
T
I
−
1
M
1
(
q
1
)
T_I^{-1}M_1(q_1)
TI−1M1(q1)意味着在第
i
i
i个部件姿态下的canonicalizing mesh,
D
D
D则表示一个标准的Chamfer Distance用于测量两个静态mesh之间的距离。其实也就是说,这个指标也就是让两个铰接物体分别获得其所有姿态下的mesh,通过逐一衡量不同铰接物体两两姿态mesh之间的距离,求得一个最小值,感觉看到这里,会认为这并不算一种特别聪明的办法,就是一种暴力破解法。两个铰接物体之间的Instantiation distance被定义为:
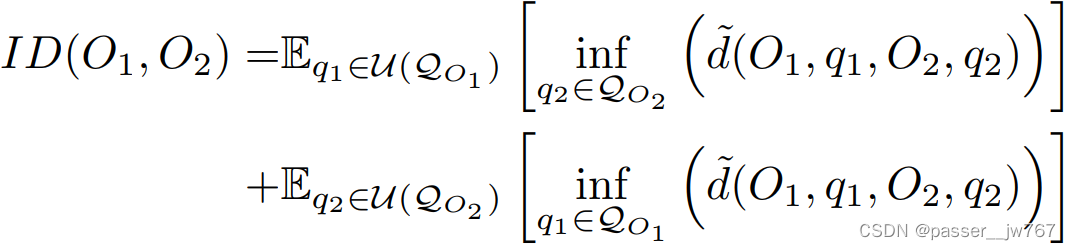
q
∈
Q
O
q∈Q_{O}
q∈QO意味着在关节范围内采样所有可能的joint pose以获得可能的kinematic structure。这个Instantiation distance实例化地测量了在所有可能的joint pose下,到另一个articulated object的最小期望距离。但这种做法在实践中是不可行的,因为有太多的计算消耗,每一个实例的articulated mesh都得计算出来,所以这里采用近似的办法,均匀地sample了M个关节状态
Q
1
=
{
q
k
∣
q
k
∈
U
(
Q
O
1
)
,
k
=
1
,
.
.
.
,
M
}
Q_1=\{q_k|q_k∈U(Q_{O_1}),k=1,...,M\}
Q1={qk∣qk∈U(QO1),k=1,...,M},并通过下式完成近似:
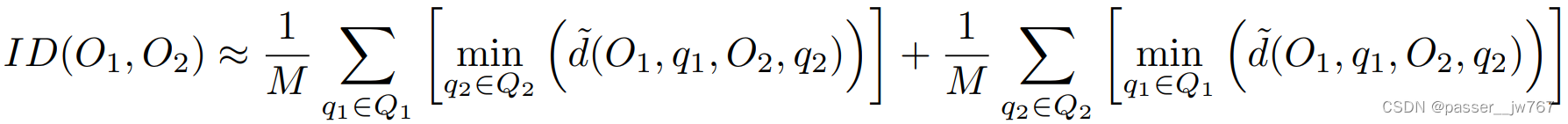
作者在论文中的所有评价均采用
M
=
10
M=10
M=10。同时采样了其他3个常见的指标:Minimum matching distance(MMD)用以匹配生成质量,coverage(COV)用于测试参考集被覆盖的多少,1-nearest neighbor accuracy(1-NNA)通过1-nn分类精度来衡量两个分布之间的距离。
NAP捕捉到的铰接物体分布质量
这就是通过文章的方法来进行铰接物体的生成,并进一步使用评价指标来进行评估。
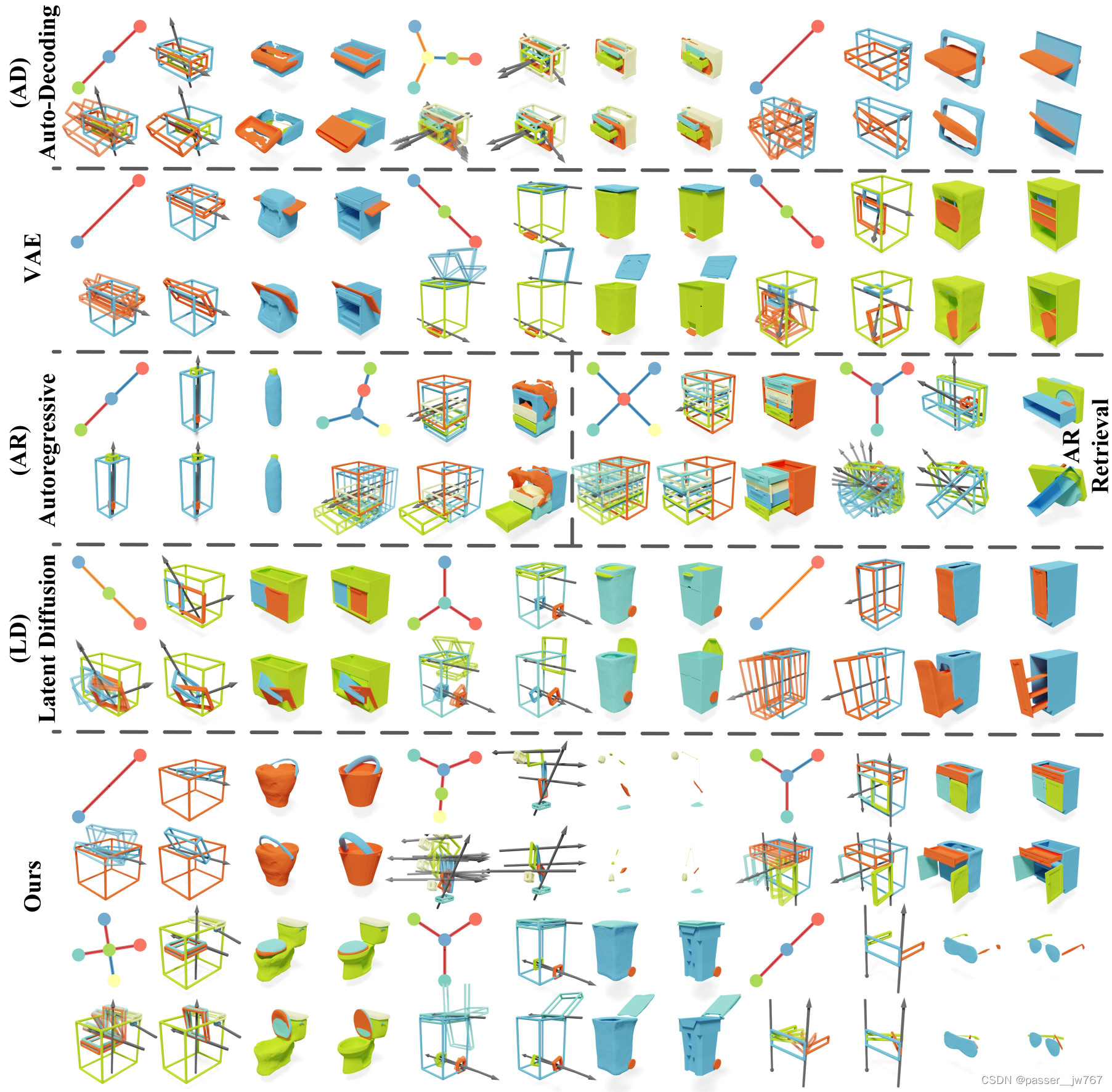
这里的baseline是在一些基于部件语义生成shape、基于场景图合成室内场景的一些方法上,equip with different generative method,例如auto-Decoding、VAE、Auto regressive、Latent Diffusion等。
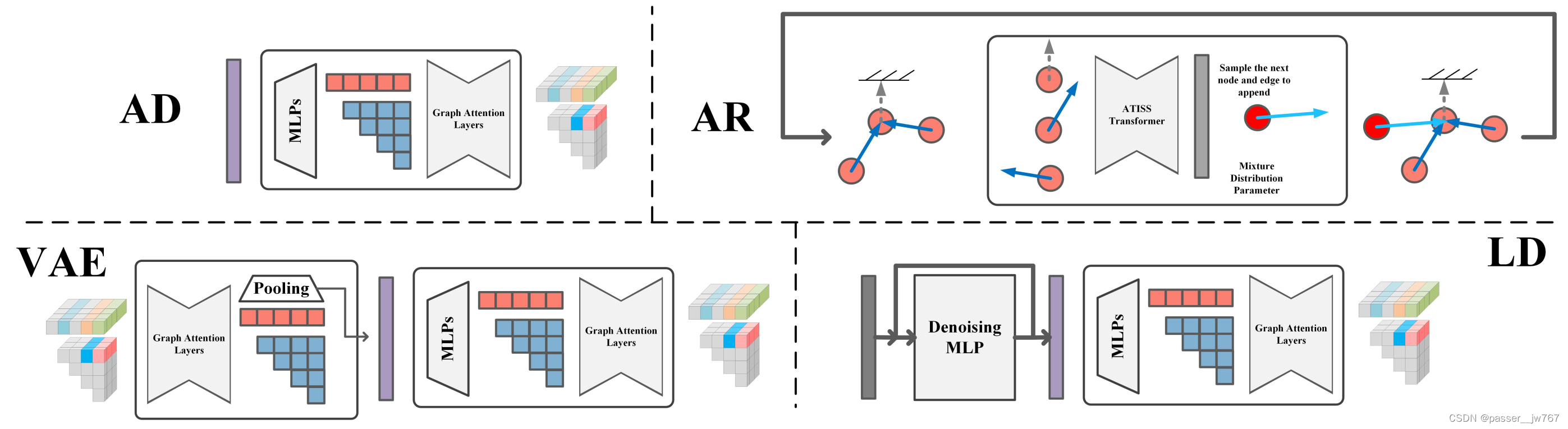
Auto-Decoding:这种方法是直接将latent code通过一组MLP解码成一组Node features和一组Edge features,将这些feature通过论文里提出的Graph Attention Layers恢复出铰接图。
VAE:输入铰接图通过Graph Attention layers处理成一个latent code,再通过解码器解码出铰接图。就是一个encoder-decoder的形式。
Autoregressive(AR):这个方法是由3D室内场景合成得到的启发,在这种室内场景合成中,在迭代中不断生成场景中的物体。这里不再使用图的表达方式,而是使用如图所示的一种表达方式,其中的每一个slots由节点本身及指向其父亲的有向边组成,根节点则指向一个虚拟边。这个ATSS transformer的目标是预测给定的生成节点和生成边的混合分布,在每一次迭代的过程中预测出append到树的slot(包含节点和边的信息)。树的增长停止也由一个indicator进行指示。
Latent Diffusion(LD):这个方法是受到3D生成中广泛运用的latent space diffusion的启发,使用类似的方法进行baseline的构建。这里的Auto-Decoder部分和上面的Auto-Decoder是一样的,这种方法和论文的方法不同之处在于网络使用了一个带有跳跃连接的巨大的MLP在紧凑的latent space空间中进行预测和操作。我认为这种方法和文章的区别就是,这个latent code表示的是global object的信息,而文章中是对一个global object中的每一个part进行latent code的预测。
NAP是否足够高效?——消融实验
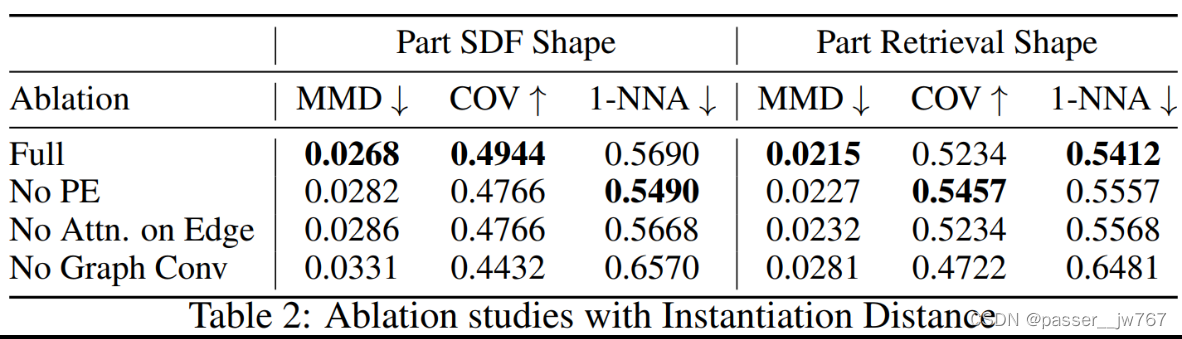
消融就是分别去除Positional Encoding位置编码、去除边注意力权重(就是去掉这种权重的计算方式)、去除Graph layer。
位置编码的重要性在于:在先前一些阶段,reverse diffusion还不能够分清楚nodes的时候,Positional Encoding位置编码能够提供帮助
边注意力权重的重要性:如果只使用平均池化的方法来作为权重,可能会导致不能够正确的聚集neighborhood的nodes信息,从而导致表现能力降低
Graph-layer的重要性:消融实验的时候使用PointNet中的全局池化层来替代,替代后,图的连接会被完全忽视,信息交换是通过全局池化进行的。
NAP可以做一些什么应用?
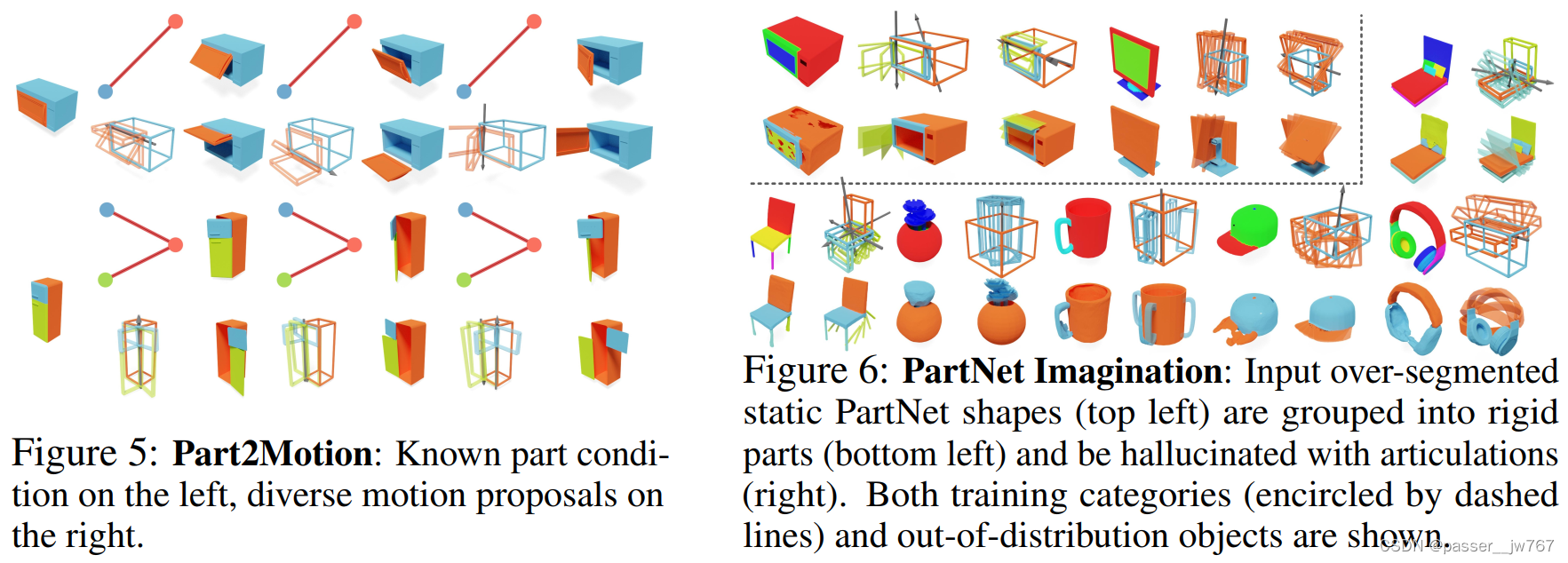

Part2Motion:证明了在已知静态部件的情况下, 使用NAP来生成kinematic structure。如Figure 5,可以生成不同的运动结构
PartNet Imagination:感觉像是对一些static object产生一些articulated的幻觉
Motion2Part:类似Part2Motion,这里是给定kinematic structure来生成static part(Node)
GAPart2Object:混合了一些Node和Edge的信息,来进一步生成其他part的一些信息,对于Edge好像是指定了axis的位置但不指定动量m,网络根据这个axis的位置生成任意的运动都是有可能的
5. 总结
Conclusion,通过几个关键字总结这篇文章:
做的事情:generation
手段:diffusion model
创新:articulation graph(一种参数化articulated object的方法),graph attention-denoising(这个不清楚是不是创新,但是是通过图注意力机制进行去噪的),Instantiation Distance(用于衡量两个铰接物体之间的Distance,一种新的度量)
限制和未来工作:
- 数据集里大部分都是具有较少parts的物体(很少有较多parts的物体),这导致生成模型偏向在一些较小的图上生成表现较好,较大的图中表现较差。进一步探索多parts的物体是有趣的研究方向
- 更加结构化的Diffusion(这个其实没太理解):diffusion可以通过引入离散化进行改进。作者提出了一些未来可行的方向:在中间步骤上应用MST,将diffusion约束到Plücker manifold下(?)
- 更强的joint condition:目前的方法里,node geometry属性会对网络有更强的影响。未来可以进一步探索加强joint condition的方法
- 进行物理合理的生成:有一些生成结果可能会违反物理规律,保证生成的结果在物理上合理也是很重要的
6. 其他补充
SE(3) transformation
这里问了一下GPT关于SE(3) transformation的信息,GPT解释如下:
SE(3) 转换是指特殊欧几里得群(Special Euclidean group)的三维版本。SE(3) 转换包括平移和旋转两个元素,用于描述三维空间中物体的位置和姿态变换。
在三维空间中,SE(3) 转换可以表示为一个 4x4 的矩阵,其中前三行前三列是旋转矩阵,表示物体的姿态变换,最后一列是平移矩阵,表示物体的位置变换。SE(3) 转换可以将一个点从一个坐标系转换到另一个坐标系,同时保持距离、角度等几何属性不变。
SE(3) 转换在计算机图形学、机器人学、计算机视觉等领域中广泛应用,用于表示物体的位姿、相机的位姿、坐标系的变换等。
Positional Encoding位置编码
参考了:【Transformer系列】深入浅出理解Positional Encoding位置编码
在这篇文章中,位置编码的运用是在网络输入的时候,通过位置编码在网络开始学习的时候为网络提供引导,我理解这里也就是通过位置编码进一步表示part和part之间的一种位置的关系,以帮助网络去理解这个铰接物体(图)


![[概率论]四小时不挂猴博士](https://img-blog.csdnimg.cn/direct/7e6584ae35264f999035dc71194491e7.png)