广义表的定义
如果允许表中的数据元素具有自身结构,即数据元素也可以是一个线性表,这就是广义表,有时也称之为列表(Lists)。
广义表是n(n≥0)个元素a1, a2, …, an的有限序列,即LS=(a1, a2, …, an)。
其中,LS是广义表的名称,n是它的长度。ai可以是单个元素,也可以是广义表。若ai是单个元素,则称它是广义表LS的原子;若ai是广义表,则称它为LS的子表。当LS非空时,称第一个元素a1为LS的表头(Head),其余元素组成的表(a2, a3,…, an)为表尾(Tail)。
举一些广义表的例子,约定大写字母表示表,小写字母表示原子:
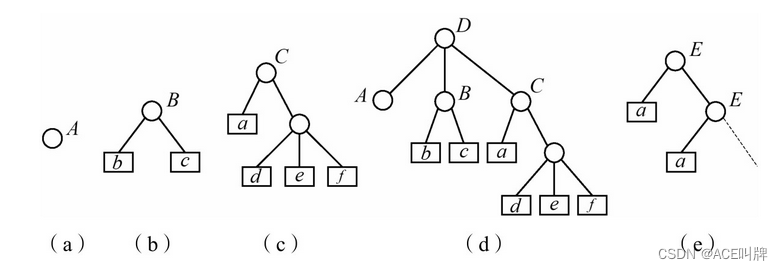
A=( ):A是一个空表,其长度为0。
B=(b, c):B是一个长度为2的列表。
C=(a, (d, e, f)):C是一个长度为2的列表,其中第一个元素是原子a,第二个元素是子表(d, e, f)。
D=(A, B, C):D是一个长度为3的列表,其中3个元素都是子表。
E=(a, E):E是一个长度为2的列表,它是一个递归表。
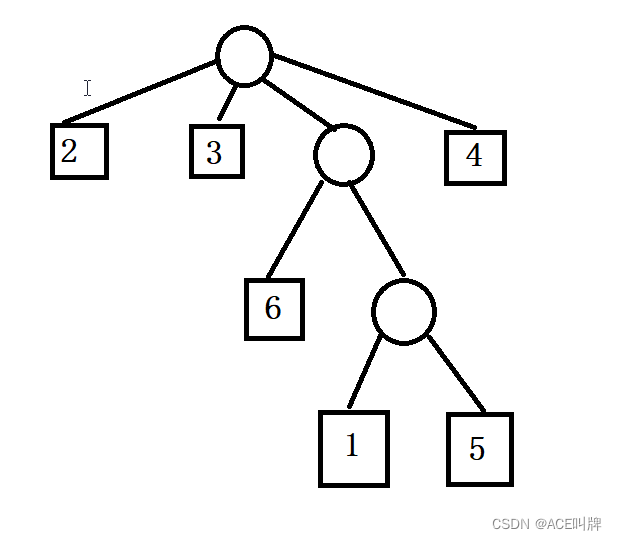
广义表可以用图形象地表示,如上述例子可以用下图表示。图中用圆圈表示广义表,用方块表示原子。
由广义表的定义可以推导出以下4个结论。
① 由于广义表中的元素可以是原子也可以是子表,因此广义表是一个多层次结构。
② 广义表是可以共享的。例如在上述例子中,广义表B是D的子表。
③ 广义表可以是其本身的一个子表,因此广义表允许递归。例如在上述例子中,广义表E是一个递归表。
④ 广义表的元素之间除了存在次序关系之外,还存在层次关系。把广义表展开后所包含的括号层数称为广义表的深度。例如,广义表C的深度为2, E的深度为∞。
广义表的操作主要有:
◉ 建立一个广义表。
◉ 判断广义表是否为空表。
◉ 判断指定数据元素是否为原子。
◉ 求广义表深度。
◉ 遍历广义表。
◉ 插入一个数据元素。
◉ 删除一个数据元素。
广义表的存储结构
由于广义表的数据元素具有不同结构,所以用顺序结构很难实现,通常采用链式结构,一个结点表示一个元素。
广义表的单链表示
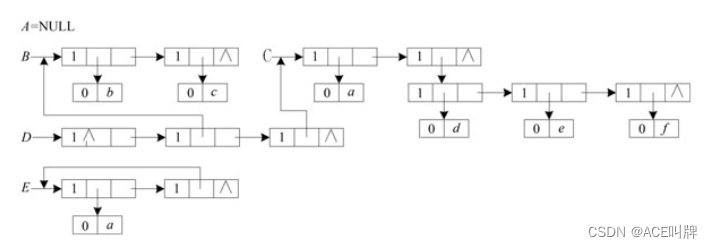
类似线性表的单链表结构,可以用单链结构存储广义表。每个结点由如下3个域组成:

其中atom是标志域,true表示该元素是原子,false表示是广义表。如果元素是原子,则next保存后继结点的地址,只使用data值;如果元素是广义表,那么sublist保存子表的第一个结点的地址,next保存后继结点的地址
广义表的节点定义:
// 广义表节点的结构定义
struct GListNode {
bool isAtom; // 是否是原子类型节点
union {
int data; // 原子类型节点的值
GListNode* sublist; // 子表类型节点的子表指针
};
GListNode* next; // 下一个节点指针
};
为什么选用union?
广义表节点可以是原子类型或子表类型,因此我们需要为节点结构体定义两个不同的属性。使用union结构体可以使节点结构体的内存使用更为紧凑,从而减小内存的占用,比使用两个不同的属性更高效。
在union结构体中,只有一个成员可以有效地保存数据,而使用布尔型的isAtom表示节点的类型,则可以使用union结构体中的另一个成员来存储节点所包含的数据。在该示例中,data成员用于存储原子类型节点的值,而sublist成员用于存储子表类型节点的子表指针。
此外,使用union结构体还可以减少代码的复杂度,使程序更加简洁易懂,提高代码的可读性和可维护性。
广义表的简单实现
#pragma once
#include <iostream>
// 广义表节点的结构定义
struct GListNode
{
bool isAtom; // 是否是原子类型节点
union
{
int data; // 原子类型节点的值
GListNode* sublist; // 子表类型节点的子表指针
};
GListNode* next; // 下一个节点指针
};
class GenTable
{
public:
// 创建原子
GListNode* CreateAtom(const int& value);
// 创建广义表
GListNode* CreateSublist(GListNode* sublist);
// 在广义表末尾添加节点
void AppendNode(GListNode*& list, GListNode* node);
// 打印广义表
void PrintGList(GListNode* list);
// 求广义表深度
int GetDepth(GListNode* node);
// 判断指定数据元素是否为原子
bool IsAtom(GListNode* node);
private:
GListNode* head_;
};
#include "GenTable.h"
GListNode* GenTable::CreateAtom(const int& value)
{
GListNode* node = new GListNode;
node->isAtom = true;
node->data = value;
node->next = nullptr;
return node;
}
GListNode* GenTable::CreateSublist(GListNode* sublist)
{
GListNode* node = new GListNode;
node->isAtom = false;
node->sublist = sublist;
node->next = nullptr;
return node;
}
void GenTable::AppendNode(GListNode*& list, GListNode* node)
{
if (list == nullptr)
list = node;
else
{
GListNode* p = list;
while (p->next)
p = p->next;
p->next = node;
}
}
void GenTable::PrintGList(GListNode* list)
{
if (list == nullptr)
{
std::cout << "空表" << std::endl;
return;
}
std::cout << "(";
GListNode* p = list;
while (p != nullptr)
{
if (p->isAtom)
std::cout << p->data;
else
PrintGList(p->sublist);
if (p->next != nullptr)
std::cout << ", ";
p = p->next;
}
std::cout << ")";
}
int GenTable::GetDepth(GListNode* node)
{
// 空表的深度为0
if (node == nullptr)
return 0;
if (node->isAtom && node->next == nullptr)
// 原子的深度为1
return 1;
else if(node->isAtom)
return GetDepth(node->next);
int maxDepth = 0;
// 遍历子表,并计算子表的深度
GListNode* sublist = node->sublist;
while (sublist != nullptr)
{
int currDepth = GetDepth(sublist);
if (currDepth > maxDepth)
maxDepth = currDepth;
sublist = sublist->next;
}
// 子表的最大深度加1
return maxDepth + 1;
}
bool GenTable::IsAtom(GListNode* node)
{
return node != nullptr && node->isAtom;
}
#include <iostream>
#include "GenTable.h"
int main()
{
GenTable table;
GListNode* list = nullptr;
GListNode* sublist = table.CreateSublist(table.CreateAtom(1));
table.AppendNode(sublist->sublist, table.CreateAtom(5));
GListNode* templist = table.CreateSublist(table.CreateAtom(6));
table.AppendNode(templist->sublist, sublist);
table.AppendNode(list, table.CreateAtom(2));
table.AppendNode(list, table.CreateAtom(3));
table.AppendNode(list, templist);
table.AppendNode(list, table.CreateAtom(4));
table.PrintGList(list);
std::cout << std::endl;
std::cout << "深度为:" << table.GetDepth(list) << std::endl;
system("pause");
return 0;
}
输出:
(2, 3, (6, (1, 5)), 4)
深度为:3