数据结构-考研难点代码突破（C++实现有向图最短路径算法（Dijkstra，Floyd-Warshall算法）图解操作细节（引自C语言中文网））

news2024/9/20 18:51:43

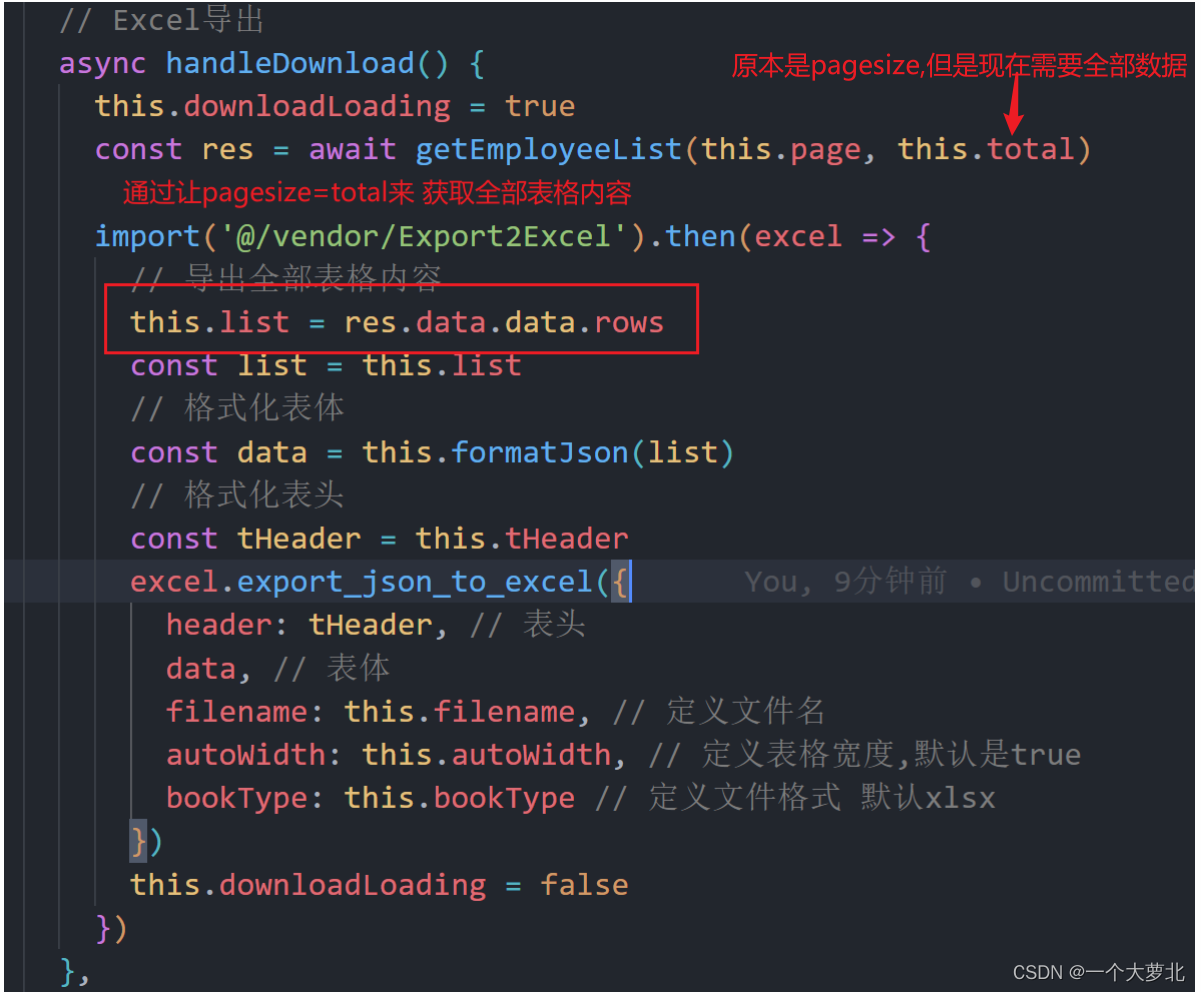
以代码的方式复习考研数据结构知识点，这里在考研不以代码为重点，而是以实现过程为重点

文章目录

  • 1. 最短路径
  • 2. 单源最短路径
    • ⅠDijkstra算法
      • C++代码
  • 3. 多源最短路径
    • Ⅰ Floyd-Warshall算法
      • C++代码

1. 最短路径

图的生成树针对的是无向图，图的最短路径一般是针对的是有向图。

之前介绍的利用广度优先搜索查找最短路径只是对无权图而言的

当图是带权图时，把从一个顶点a到图中其余任意一个顶点x的一条路径（可能不止一条）所经过边上的权值之和，定义为该路径的带权路径长度，把带权路径长度最短的那条路径称为最短路径.

求解最短路径的算法通常都依赖于一种性质，即两点之间的最短路径也包含了路径上其他顶点间的最短路径。

带权有向图G的最短路径问题一般可分为两类∶

  1. 是单源最短路径，即求图中某一顶点到其他各顶点的最短路径，可通过经典的 Dijkstra（迪杰斯特拉），Bellman-Ford（）算法求解
  2. 是多源最短路径，即求每对顶点间的最短路径，可通过Floyd（弗洛伊德）算法来求解

2. 单源最短路径

单源最短路径问题：给定一个有向图G = < V ， E > ，求源结点s ∈ V到图中每个结点v ∈ V 的最短路径给一个点A，A点到图的其他点的最短路径。

ⅠDijkstra算法

Dijkstra算法适用于解决带权重的有向图上的单源最短路径问题，同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点 和一个终点，所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。

如果出现权值为负数的单源最短路径问题，只能使用Bellman-Ford算法。

算法思路：C语言中文网
eg：
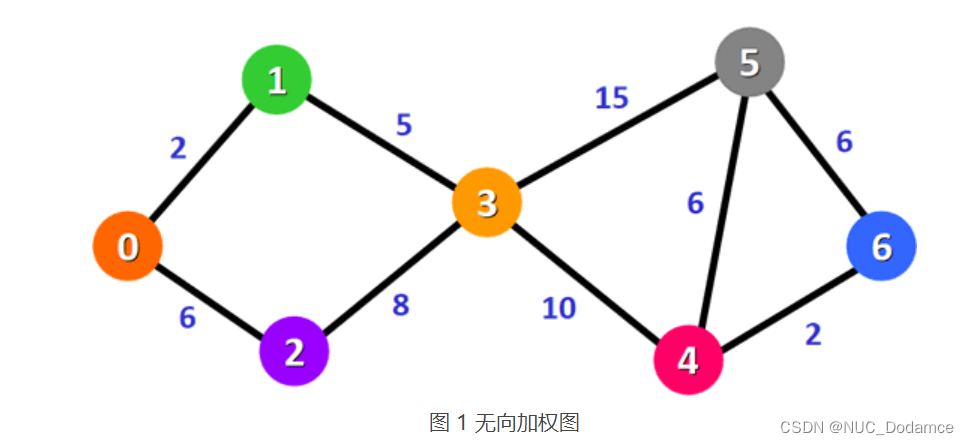
在这里插入图片描述
如上图，假设需要统计顶点0到其他顶点的最短路径

如果两个顶点之间无法直达，对应的权值为无穷大，用∞ 表示

  1. 统计从顶点 0 直达其它顶点的权值
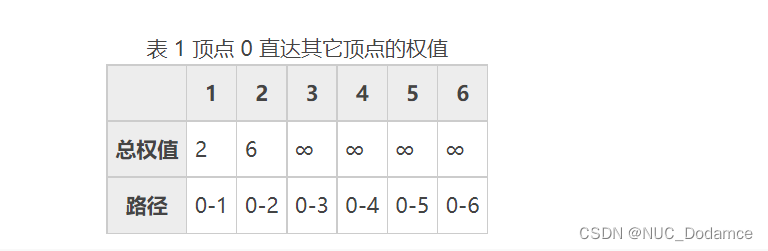
    在这里插入图片描述
  2. 表 1 中，权值最小的是 0-1 路径，它也是从顶点 0 到顶点 1 的最短路径（如图 2 所示）。原因很简单，从顶点 0 出发一共只有 0-1 和 0-2 两条路径，0-2 的权值本就比 0-1 大，所以从 0-2 出发不可能找得到比 0-1 权值更小的路径
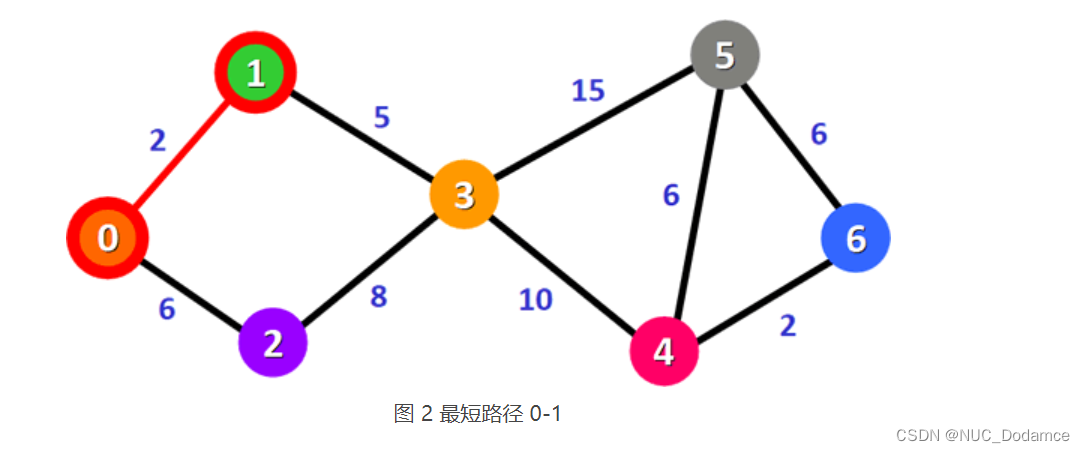
    在这里插入图片描述
  3. 找到最短路径 0-1 后，沿 0-1 路径方向查找更短的到达其它顶点的路径，并对表 1 进行更新。
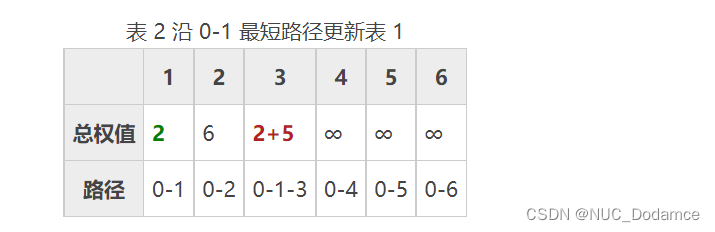
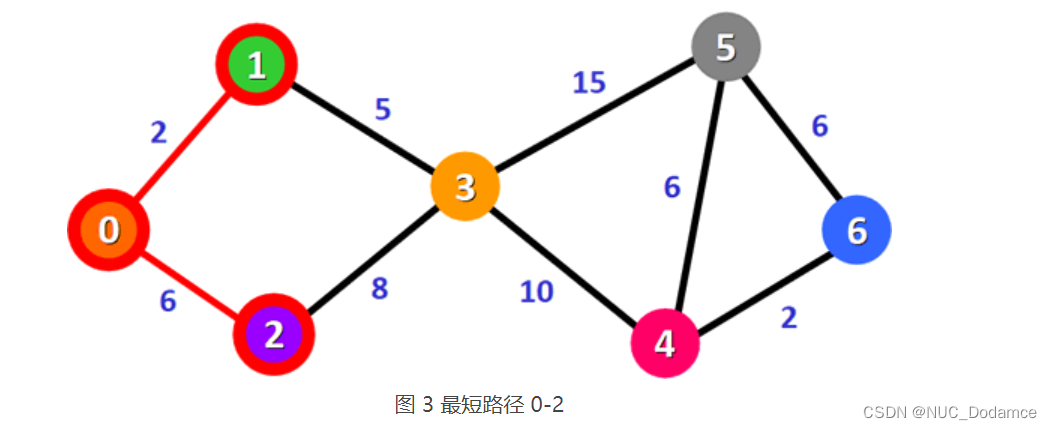
    在这里插入图片描述
    更新后的表格如表 2 所示，沿 0-1 路径可以到达顶点 3，且 0-1-3 的总权值比 0-3 更小。表 2 中，总权值最小的路径是 0-2，它也是从顶点 0 到顶点 2 的最短路径，如下图所示
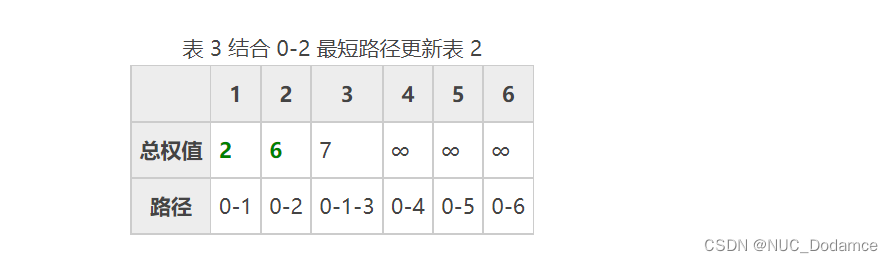
    在这里插入图片描述
  4. 重复之前的操作，沿 0-2 路径方向查找更短的到达其它顶点的路径。遗憾地是，从顶点 2 只能到达顶点 3，且 0-2-3 的总权值比表 2 中记录的 0-1-3 更大，因此表 2 中记录的数据维持不变。
    在这里插入图片描述
    总权值最小的是 0-1-3，它也是顶点 0 到顶点 3 的最短路径。
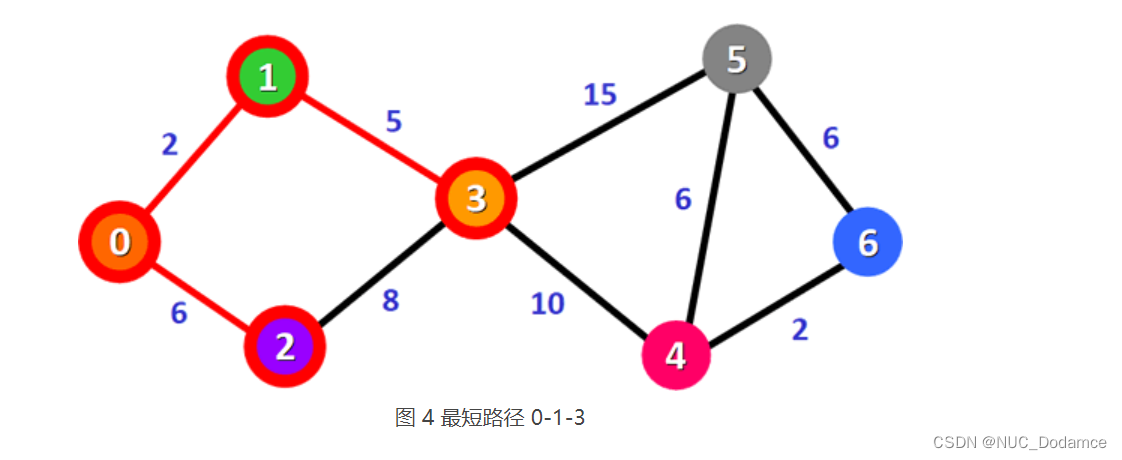
    在这里插入图片描述
    沿 0-1-3 路径方向，查找到其它顶点更短的路径并更新表 3。更新后的表格为：
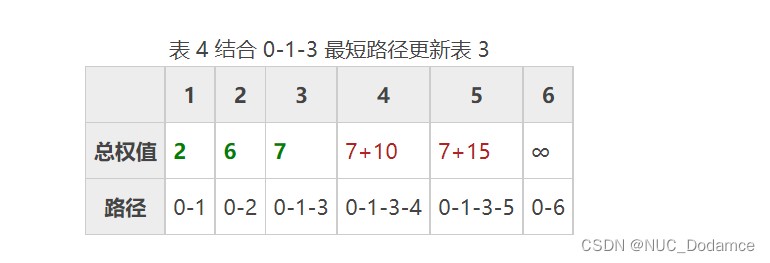
    在这里插入图片描述
  5. 表 4 中，总权值最小的是 0-1-3-4，它是顶点 0 到顶点 4 的最短路径。
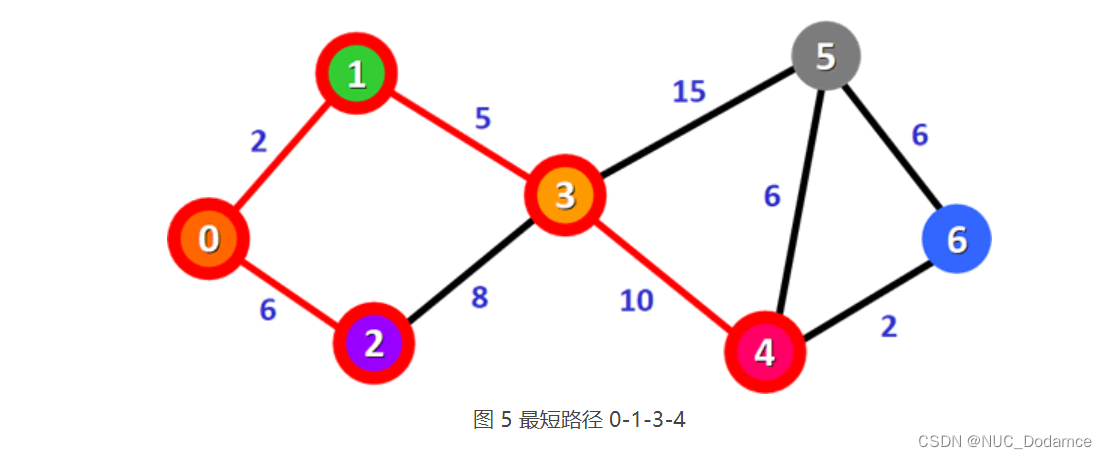
    在这里插入图片描述
    从顶点 4 出发，查找顶点 0 到其它顶点更短的路径并更新表 4。更新后的表格为：
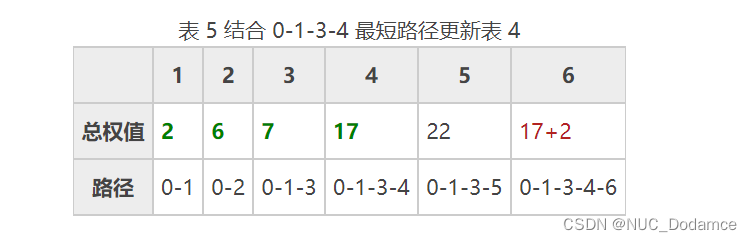
    在这里插入图片描述
  6. 表 5 中，总权值最小的路径是 0-1-3-4-6，它是顶点 0 到顶点 6 的最短路径。
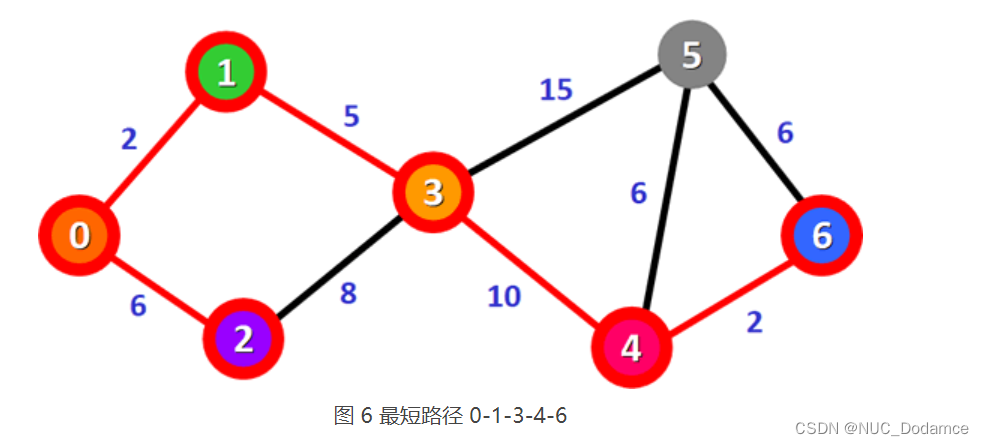
    在这里插入图片描述
  7. 从图 6 可以看到，只剩下顶点 0 到顶点 5 的最短路径尚未确定。从顶点 6 出发到达顶点 5 的路径是 0-1-3-4-6-5，对应的总权值为 25，大于表 5 中记录的 0-1-3-5 路径，因此 0-1-3-5 是顶点 0 到顶点 5 的最短路径。
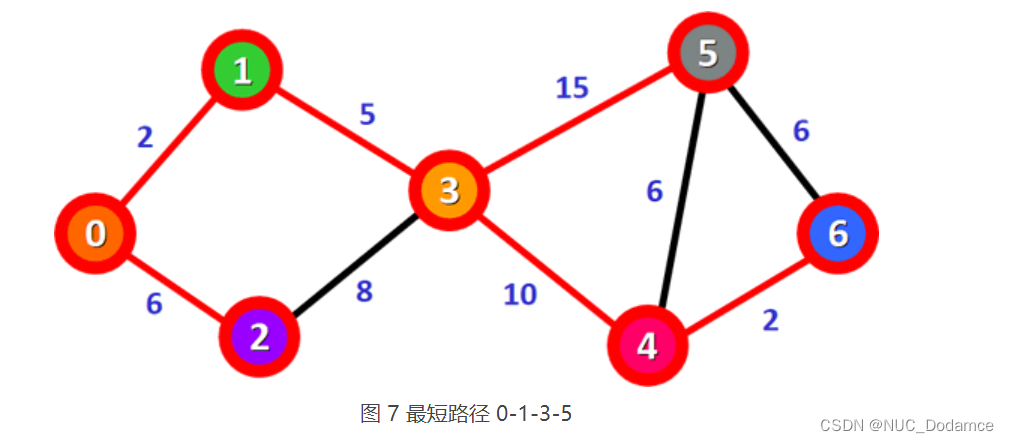
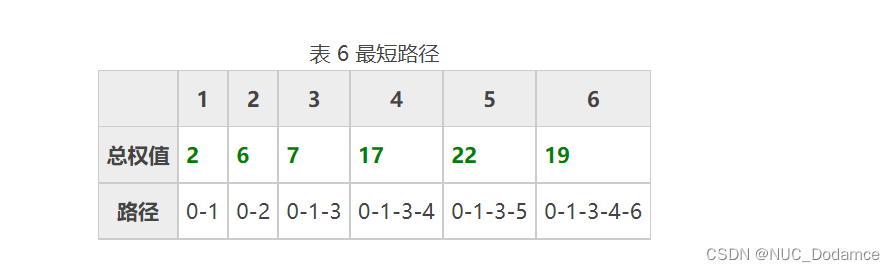
    在这里插入图片描述

最终，通过Dijkstra算法计算出0到图其他节点的最短路径为：
在这里插入图片描述

C++代码

这里使用邻接矩阵保存边关系

顶点保存在dist数组中，数组下标代表顶点编号，数组下标值代表源顶点到这个顶点的最短路径长度。初始化默认值（无穷）

为了保存最短路径之间的节点，这里使用数组pPath的形式保存每一个顶点的父节点。（存储的是路径中所有顶点最短路径的前一个顶点下标）数组初始化为-1。
类似并查集找根节点的过程

Dijkstra算法

// 邻接矩阵法存储图结构

#include <iostream>
#include <assert.h>
#include <map>
#include <vector>
#include <queue>
#include <algorithm>

// v:图顶点保存的值。w:边的权值 max:最大权值，代表无穷。flag=true代表有向图。否则就是无向图
template <class v, class w, w max = INT_MAX, bool flag = false>
class graph
{
private:
    std::vector<v> _verPoint;            // 顶点集合
    std::map<v, int> _indexMap;          // 顶点与下标的映射
    std::vector<std::vector<w>> _matrix; // 邻接矩阵

    int _getPosPoint(const v &point)
    {
        if (_indexMap.find(point) != _indexMap.end())
        {
            return _indexMap[point];
        }
        else
        {
            std::cout << point << " not found" << std::endl;
            return -1;
        }
    }

public:
    graph() = default;
    // 根据数组来开辟邻接矩阵
    graph(const std::vector<v> &src)
    {
        _verPoint.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _verPoint[i] = src[i];
            _indexMap[src[i]] = i;
        }

        // 初始化邻接矩阵
        _matrix.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _matrix[i].resize(src.size(), max);
        }
    }
    // 添加边的关系,输入两个点，以及这两个点连线边的权值。
    void AddEdge(const v &pointA, const v &pointB, const w &weight)
    {
        // 获取这个顶点在邻接矩阵中的下标
        int posA = _getPosPoint(pointA);
        int posB = _getPosPoint(pointB);
        _matrix[posA][posB] = weight;
        if (!flag)
        {
            // 无向图,邻接矩阵对称
            _matrix[posB][posA] = weight;
        }
    }

    // 打印邻接矩阵
    void PrintGraph()
    {
        // 打印顶点对应的坐标
        typename std::map<v, int>::iterator pos = _indexMap.begin();
        while (pos != _indexMap.end())
        {
            std::cout << pos->first << ":" << pos->second << std::endl;
            pos++;
        }
        std::cout << std::endl;

        // 打印边
        printf("  ");
        for (int i = 0; i < _verPoint.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
        }
        printf("\n");

        for (int i = 0; i < _matrix.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
            for (int j = 0; j < _matrix[i].size(); j++)
            {
                if (_matrix[i][j] == max)
                {
                    // 这条边不通
                    printf("∞ ");
                }
                else
                {
                    std::cout << _matrix[i][j] << " ";
                }
            }
            printf("\n");
        }
        printf("\n");
    }

    //-------------------------------Dijkstra---------------------------
    /**
     * @brief 单源最短路径
     *
     * @param src 起点
     * @param dist dist保存src到各个顶点的最短距离
     * @param pPath pPath:保存最短路径的节点对应下标
     */
    void Dijkstra(const v &src, std::vector<w> &dist, std::vector<int> &pPath)
    {
        size_t pos = _getPosPoint(src);
        size_t size = _verPoint.size();
        pPath.resize(size, -1);
        dist.resize(size, max);

        dist[pos] = 0;    // 源顶点到自己本身最短距离为0
        pPath[pos] = pos; // 源顶点的最短路径的父节点是自己本身

        std::vector<bool> S(size, false); // 已经确定最短路径的顶点的集合

        for (size_t time = 0; time < size; time++)
        {
            // 选不在S集合 最短路径的顶点，更新其他路径
            int p = 0;
            w min = max;

            for (size_t i = 0; i < size; i++)
            {
                if (S[i] == false && dist[i] < min)
                {
                    p = i;
                    min = dist[i];
                }
            }

            // 把p放到S集合中
            S[p] = true;

            // src->p + p->p邻接节点 与 src ->p邻接节点权值相比较小，要更新
            for (size_t adP = 0; adP < size; adP++)
            {
                // 找到p点邻接顶点
                if (S[adP] == false && _matrix[p][adP] != max)
                {
                    if ((dist[p] + _matrix[p][adP]) < dist[adP])
                    {
                        dist[adP] = dist[p] + _matrix[p][adP];

                        // 更新最短路径父节点
                        pPath[adP] = p;
                    }
                }
            }
        }
    }

    /**
     * @brief 单源最短路径
     *
     * @param src 起点
     * @param dist dist保存src到各个顶点的最短距离
     */
    void Dijkstra(const v &src, std::vector<w> &dist)
    {
        std::vector<int> pPath;
        Dijkstra(src, dist, pPath);

        size_t pos = _getPosPoint(src);
        size_t size = _verPoint.size();
        for (size_t i = 0; i < size; i++)
        {
            if (i != pos)
            {
                std::vector<int> path;
                size_t dst_pos = i;
                std::cout << "最短路径为:";
                while (dst_pos != pos)
                {
                    path.push_back(dst_pos);
                    dst_pos = pPath[dst_pos];
                }
                path.push_back(pos);
                std::reverse(path.begin(), path.end());
                for (size_t j = 0; j < path.size(); j++)
                {
                    std::cout << _verPoint[path[j]];
                    if (j != path.size() - 1)
                    {
                        std::cout << "->";
                    }
                }
                std::cout << "长度: " << dist[i] << std::endl;
            }
        }
    }
};

#include "Dijkstra.h"

using namespace std;

int main(int argc, char const *argv[])
{
    graph<char, int> g({'0', '1', '2', '3', '4', '5', '6'});
    g.AddEdge('0', '1', 2);
    g.AddEdge('0', '2', 6);
    g.AddEdge('1', '3', 5);
    g.AddEdge('2', '3', 8);
    g.AddEdge('3', '5', 15);
    g.AddEdge('3', '4', 10);
    g.AddEdge('4', '5', 6);
    g.AddEdge('4', '6', 2);
    g.AddEdge('6', '5', 6);
    g.PrintGraph();

    vector<int> dist;
    g.Dijkstra('0', dist);

    return 0;
}

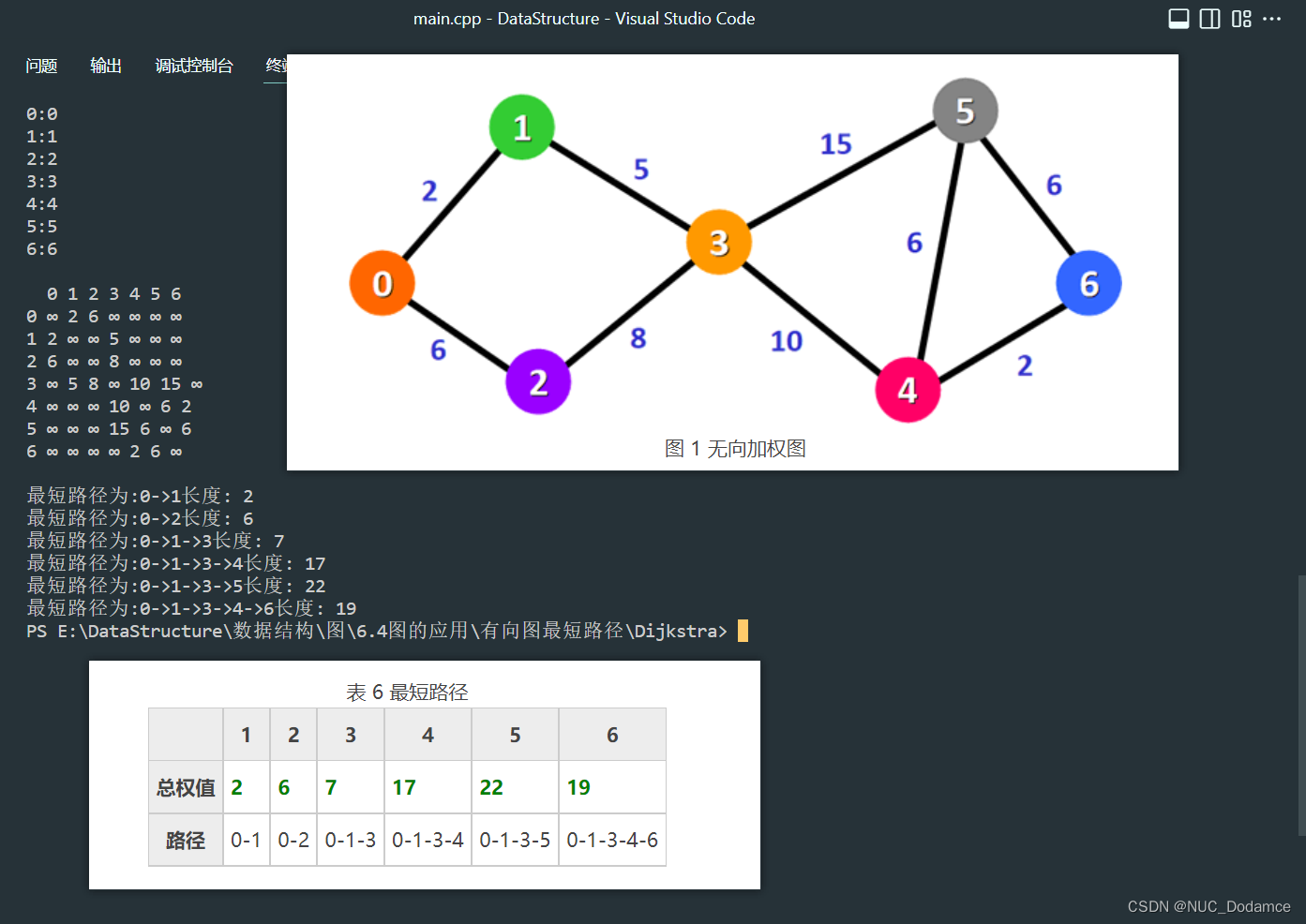
在这里插入图片描述
算法的时间复杂度为O(N2)，空间复杂度O(N)（N为顶点个数）

此外Dijkstra算法不适用于带负值的权值，使用于带负权的有向图最短路径算法为Bellman-Ford算法

3. 多源最短路径

多源最短路径：源顶点是图中的所有顶点，求图中任意两点的最短路径。

Ⅰ Floyd-Warshall算法

注意：

  1. Floyd-Warshall可以解决负数权值问题。
  2. 如果以所有点为源点，使用Dijkstra算法也可以算出图中任意两点的最短路径。但是Dijkstra算法不能带负数权值，Bellman-Ford算法效率太低。

Floyd-Warshall算法：
因为Floyd-Warshall算法要以图中任意顶点为源顶点。
根据上面分析可知，dist（记录源顶点到其他顶点的最短路径）数组应该是二维数组。
pPath（通过双亲表示法记录最短路径的节点）也应该是二维数组。

算法的思路是通过动态规划得出的。
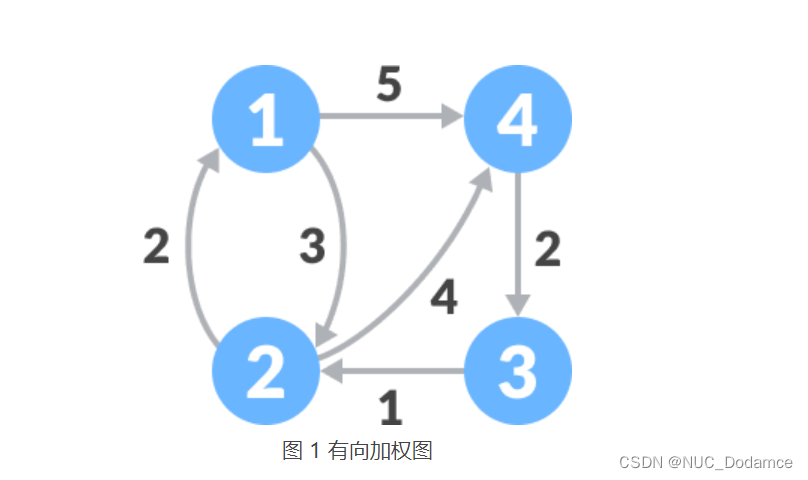
eg：
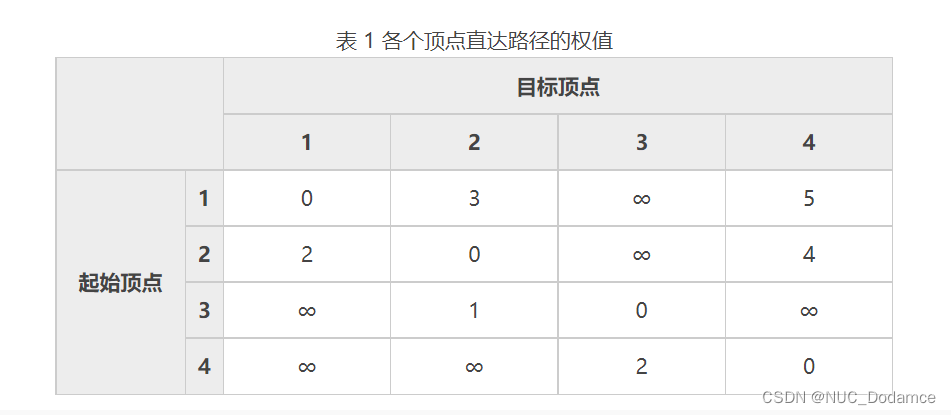
在这里插入图片描述

  1. 建立一张表格，记录每个顶点直达其它所有顶点的权值：
    在这里插入图片描述

  2. 在表 1 的基础上，将顶点 1 作为 “中间顶点”，计算从各个顶点出发途径顶点 1 再到达其它顶点的权值，如果比表 1 中记录的权值更小，证明两个顶点之间存在更短的路径，对表 1 进行更新。

    从各个顶点出发，途径顶点 1 再到达其它顶点的路径以及对应的权值分别是：
    2-1-3：权值为 2 + ∞ = ∞，表 1 中记录的 2-3 的权值也是 ∞；
    2-1-4：权值为 2 + 5 = 7，表 1 中记录的 2-4 的权值是 4；
    3-1-2：权值为 ∞ + 3，表 1 中记录的 3-2 的权值是 1；
    3-1-4：权值为 ∞ + 5，表 1 中记录的 3-4 的权值是 ∞；
    4-1-2：权值为 ∞ + 3，表 1 中记录的 4-2 的权值是 ∞；
    4-1-3：权值为 ∞ + ∞，表 1 中记录的 4-3 的权值是 2。

    以上所有的路径中，没有比表 1 中记录的权值最小的路径，所以不需要对表 1 进行更新。

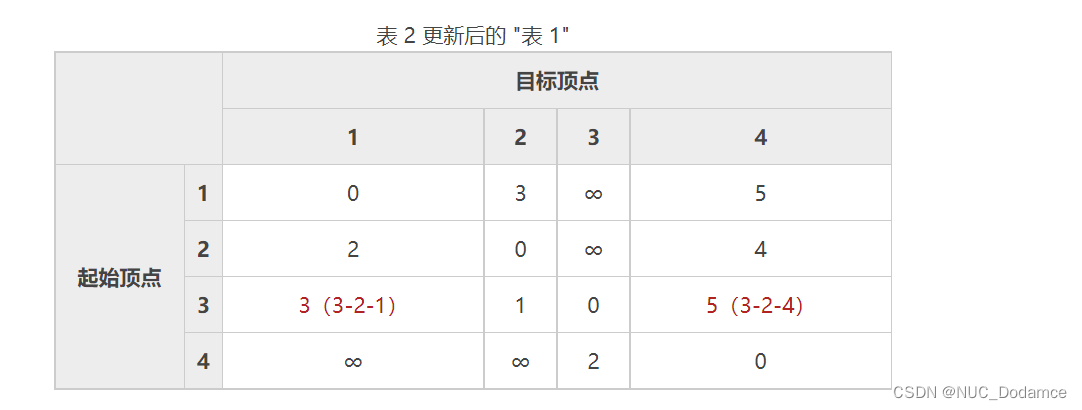
  3. 在表 1 的基础上，以顶点 2 作为 “中间顶点”，计算从各个顶点出发途径顶点 2 再到达其它顶点的权值：

    1-2-3：权值为 3 + ∞，表 1 中记录的 1-3 的权值为 ∞；
    1-2-4：权值为 3 + 4 = 7，表 1 中 1-4 的权值为 5；
    3-2-1：权值为 1 + 2 = 3，表 1 中 3-1 的权值为 ∞，3 < ∞；
    3-2-4：权值为 1 + 4 = 5，表 1 中 3-4 的权值为 ∞，5 < ∞；
    4-2-1：权值为 ∞ + 2，表 1 中 4-1 的权值为 ∞；
    4-2-3：权值为 ∞ + ∞，表 1 中 4-3 的权值为 2。

    以顶点 2 作为 “中间顶点”，我们找到了比 3-1、3-4 更短的路径，对表 1 进行更新：
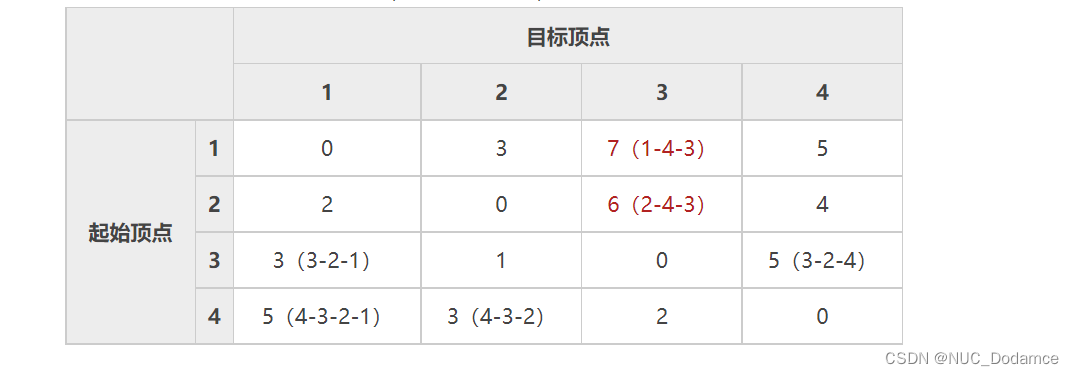
    在这里插入图片描述

  4. 以此类推，分别以不同顶点为中间顶点，不断更新表，最终更新结果为

在这里插入图片描述

C++代码

时间复杂度：O(N3)，空间复杂度O(N)

// 邻接矩阵法存储图结构

#include <iostream>
#include <assert.h>
#include <map>
#include <vector>
#include <queue>
#include <algorithm>

// v:图顶点保存的值。w:边的权值 max:最大权值，代表无穷。flag=true代表有向图。否则就是无向图
template <class v, class w, w max = INT_MAX, bool flag = false>
class graph
{
private:
    std::vector<v> _verPoint;            // 顶点集合
    std::map<v, int> _indexMap;          // 顶点与下标的映射
    std::vector<std::vector<w>> _matrix; // 邻接矩阵

    int _getPosPoint(const v &point)
    {
        if (_indexMap.find(point) != _indexMap.end())
        {
            return _indexMap[point];
        }
        else
        {
            std::cout << point << " not found" << std::endl;
            return -1;
        }
    }

public:
    graph() = default;
    // 根据数组来开辟邻接矩阵
    graph(const std::vector<v> &src)
    {
        _verPoint.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _verPoint[i] = src[i];
            _indexMap[src[i]] = i;
        }

        // 初始化邻接矩阵
        _matrix.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _matrix[i].resize(src.size(), max);
        }
    }
    // 添加边的关系,输入两个点，以及这两个点连线边的权值。
    void AddEdge(const v &pointA, const v &pointB, const w &weight)
    {
        // 获取这个顶点在邻接矩阵中的下标
        int posA = _getPosPoint(pointA);
        int posB = _getPosPoint(pointB);
        _matrix[posA][posB] = weight;
        if (!flag)
        {
            // 无向图,邻接矩阵对称
            _matrix[posB][posA] = weight;
        }
    }

    // 打印邻接矩阵
    void PrintGraph()
    {
        // 打印顶点对应的坐标
        typename std::map<v, int>::iterator pos = _indexMap.begin();
        while (pos != _indexMap.end())
        {
            std::cout << pos->first << ":" << pos->second << std::endl;
            pos++;
        }
        std::cout << std::endl;

        // 打印边
        printf("  ");
        for (int i = 0; i < _verPoint.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
        }
        printf("\n");

        for (int i = 0; i < _matrix.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
            for (int j = 0; j < _matrix[i].size(); j++)
            {
                if (_matrix[i][j] == max)
                {
                    // 这条边不通
                    printf("∞ ");
                }
                else
                {
                    std::cout << _matrix[i][j] << " ";
                }
            }
            printf("\n");
        }
        printf("\n");
    }

    //-------------------------------Floyd-Warshall---------------------------
    /**
     * @brief 多源最短路径
     *
     * @param vDist （记录源顶点到其他顶点的最短路径）数组应该是二维数组。
     * @param vPath （通过双亲表示法记录最短路径的节点）也应该是二维数组。
     */
    void FloydWarShall(std::vector<std::vector<w>> &vDist, std::vector<std::vector<int>> &vPath)
    {
        size_t size = _verPoint.size();

        // 初始化顶点距离矩阵和路径矩阵
        vDist.resize(size);
        vPath.resize(size);
        for (size_t i = 0; i < size; i++)
        {
            vDist[i].resize(size, max);
            vPath[i].resize(size, -1);
        }

        // 直接相连的边更新初始化

        for (size_t i = 0; i < size; i++)
        {
            for (size_t j = 0; j < size; j++)
            {
                if (_matrix[i][j] != max)
                {
                    vDist[i][j] = _matrix[i][j];
                    vPath[i][j] = i; // i->j起点是i点
                }
                if (i == j)
                {
                    vDist[i][j] = w();
                }
            }
        }

        // 最短路径的更新i->{其他顶点}->j
        // k作为中间点，尝试更新i->j的路径
        for (size_t k = 0; k < size; k++)
        {
            for (size_t i = 0; i < size; i++)
            {
                for (size_t j = 0; j < size; j++)
                {
                    if (vDist[i][k] != max && vDist[k][j] != max)
                    {
                        if (vDist[i][k] + vDist[k][j] < vDist[i][j])
                        {
                            // 经过k点更短，更新长度
                            vDist[i][j] = vDist[i][k] + vDist[k][j];
                            // 修改父亲节点
                            // 找上一个与j邻接的节点
                            // k->j 如果k与j直接相连，则vPath[i][j]=k
                            // 但是k->j不一定直接相连 k->...->x->j则vPath[i][j]=x,就是vPath[k][j]
                            vPath[i][j] = vPath[k][j];
                        }
                    }
                }
            }
        }
    }

    void _PrintShortLine(const v &src, std::vector<w> &dist, std::vector<int> pPath)
    {
        size_t pos = _getPosPoint(src);
        size_t size = _verPoint.size();
        for (size_t i = 0; i < size; i++)
        {
            if (i != pos)
            {
                std::vector<int> path;
                size_t dst_pos = i;
                std::cout << "最短路径为:";
                while (dst_pos != pos)
                {
                    path.push_back(dst_pos);
                    dst_pos = pPath[dst_pos];
                }
                path.push_back(pos);
                std::reverse(path.begin(), path.end());
                for (size_t j = 0; j < path.size(); j++)
                {
                    std::cout << _verPoint[path[j]];
                    if (j != path.size() - 1)
                    {
                        std::cout << "->";
                    }
                }
                std::cout << "长度: " << dist[i] << std::endl;
            }
        }
    }

    void PrintFloyd(std::vector<std::vector<w>> &vDist, std::vector<std::vector<int>> &vPath)
    {
        FloydWarShall(vDist, vPath);

        for (int i = 0; i < _verPoint.size(); i++)
        {
            _PrintShortLine(_verPoint[i], vDist[i], vPath[i]);
            std::cout << "\n";
        }
    }
};

#include "Floyd-Warshall.h"

using namespace std;

int main(int argc, char const *argv[])
{
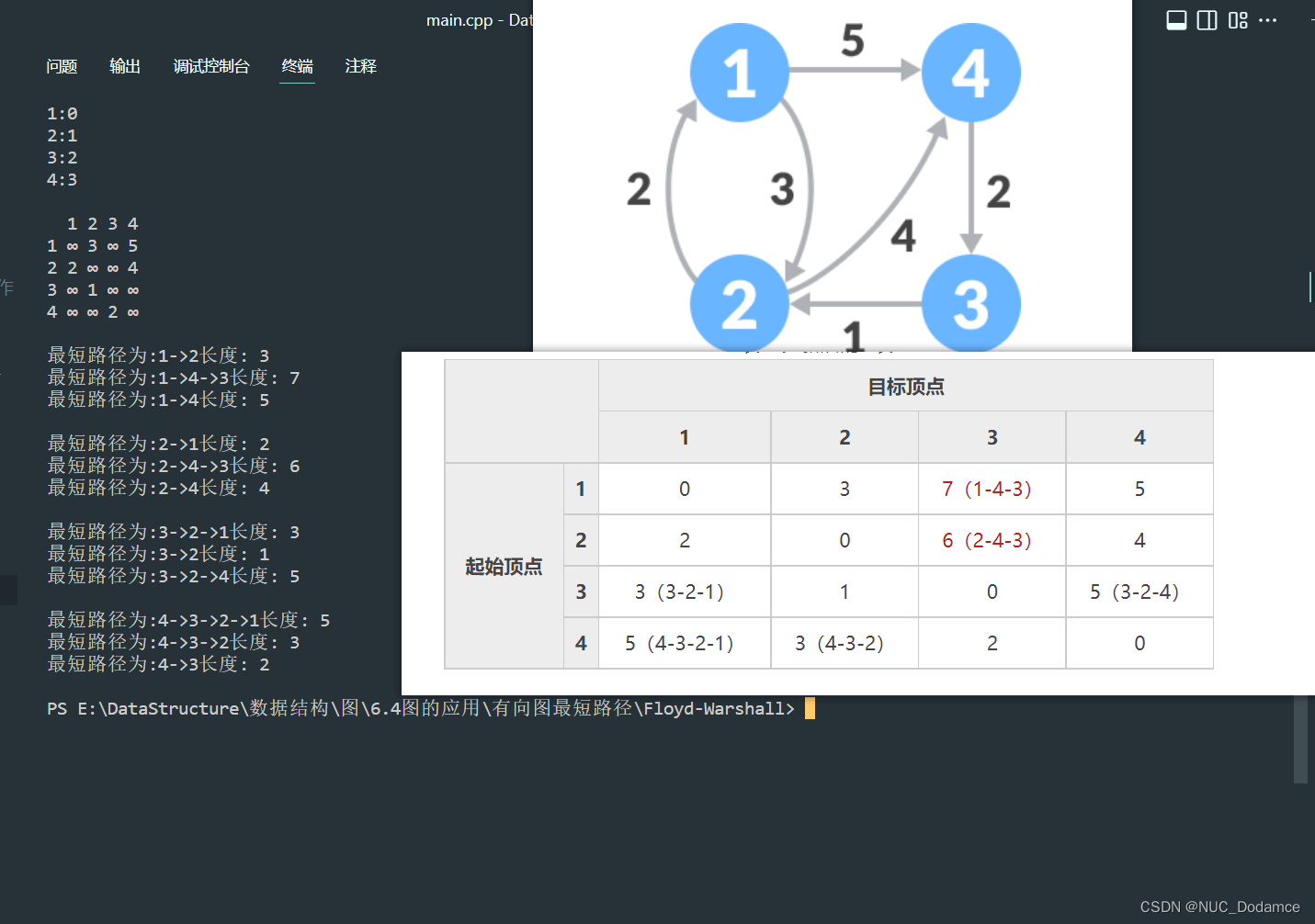
    graph<char, int, INT_MAX, true> g({'1', '2', '3', '4'});
    g.AddEdge('1', '2', 3);
    g.AddEdge('1', '4', 5);
    g.AddEdge('2', '1', 2);
    g.AddEdge('4', '3', 2);
    g.AddEdge('2', '4', 4);
    g.AddEdge('3', '2', 1);
    g.PrintGraph();

    vector<vector<int>> vDist;
    vector<vector<int>> vPath;
    g.FloydWarShall(vDist, vPath);
    g.PrintFloyd(vDist, vPath);
    return 0;
}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/135101.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

error ‘for’ loop initial declarations are only allowed in C99 mode的报错原因和两种解决办法

error ‘for’ loop initial declarations are only allowed in C99 mode的报错原因和两种解决办法

error: ‘for’ loop initial declarations are only allowed in C99 mode的报错原因和两种解决办法 for(int i0;i<5;i) { … } 错误&#xff1a;使用gcc编译代码报错 &#xff1a;error: ‘for’ loop initial declarations are only allowed in C99 mode note: use …
阅读更多...
Spark02: Spark三种任务提交方式

Spark02: Spark三种任务提交方式

1. 直接在IDEA中执行&#xff0c;方便在本地环境调试代码 2. 使用spark-submit提交到集群执行【实际工作中使用】 3. 使用spark-shell&#xff0c;方便在集群环境调试代码 比如&#xff1a;需要连接数据库&#xff0c;无法在本地调试的情况。 spark-shell 实现了用户可以逐…
阅读更多...
流程控制之for循环练习

流程控制之for循环练习

目录练习案例1. for创建20用户2. for ping测试指网段的主机3. 使用for实现批量主机root密码的修改练习案例 1. for创建20用户 用户前缀由用户输入 用户初始密码由用户输入 例如&#xff1a;test01,test10 #!/bin/bash ######################### #File name:userCreate.sh #…
阅读更多...
[学习笔记]2021韩顺平一周学会Linux

[学习笔记]2021韩顺平一周学会Linux

文章目录视频链接&#xff1a;第1章&#xff1a;Linux开山篇-内容介绍1.1 本套Linux课程内容1.2 Linux使用的地方1.3 Linux应用的领域第2章&#xff1a;Linux基础篇-Linux入门&#xff1a;2.1 Linux介绍2.1.1概述2.2 Linux和Unix的关系2.2.1 Unix是怎么来的2.2.2 Linux是怎么来…
阅读更多...
【阶段一】Python快速入门06篇：正则表达式-re 模块

【阶段一】Python快速入门06篇：正则表达式-re 模块

本篇的思维导图： 正则表达式-re 模块 正则表达式(Regular Expression)是一种文本模式的描述方法。例如，\d是一个正则表达式，表示一位数字字符，即任何一位0到9的数字。 在 Python 语言中re 模块提供了全部的正则表达式函数，例如：compile 函数。 compile 函数 compile 函…
阅读更多...
Qt CSV文件的创建，读写操作

Qt CSV文件的创建，读写操作

文章目录一.CSV文件介绍二.创建CSV文件三.写入CSV文件四.读取CSV文件一.CSV文件介绍 逗号分隔值&#xff08;Comma-Separated Values&#xff0c;CSV&#xff0c;有时也称为字符分隔值&#xff0c;因为分隔字符也可以不是逗号&#xff09;&#xff0c;其文件以纯文本形式存储表…
阅读更多...
基于ASP.NET MVC的运动用品网上销售系统

基于ASP.NET MVC的运动用品网上销售系统

摘要 随着现代都市生活节奏的不断加快、网络覆盖面的日益扩大&#xff0c;越来越多的人们加入了网上购物的行列。如今&#xff0c;网购已经成为人们生活的一部分。本系统主要是使用 B/S架构开发出的一个基于ASP.NET的运动用品网上销售系统。前台页面使用htmljscss&#xff0c;S…
阅读更多...
Freemarker指令语法

Freemarker指令语法

基础语法种类 1、注释&#xff0c;即<#-- -->&#xff0c;介于其之间的内容会被freemarker忽略 <#--我是一个freemarker注释-->2、插值&#xff08;Interpolation&#xff09;&#xff1a;即..部分,freemarker会用真实的值代替{..}部分,freemarker会用真实的值代…
阅读更多...
十一、中间件的使用

十一、中间件的使用

Express的应用本质上就是调用各种中间件&#xff0c;中间件指的是业务流程中的中间处理环节&#xff0c;服务器的生命周期一般是 接收 —— 处理 —— 响应&#xff1b;那么中间件就充当处理的角色&#xff0c;它其实就是一个函数&#xff0c;该函数除了能够访问请求对象req和响…
阅读更多...
TC275——02板卡简单介绍

TC275——02板卡简单介绍

前部 核心&#xff1a;英飞凌 32位 AURIXTC275 TriCore核 开发工具&#xff1a; AURIX™Development Studio、FreeEntryToolchain CPU&#xff1a; 最大频率&#xff1a;200M外部晶振&#xff1a;20MFPU&#xff1a;支持封装&#xff1a;LQFP176-22 FLASH&#xff1a;4M D…
阅读更多...
高并发系统设计 -- 性能测试

高并发系统设计 -- 性能测试

响应时间&#xff1a;是客户发出请求到得到响应的整个过程的时间。 网络传输时间&#xff1a;N1N2N3N4应用服务器处理时间&#xff1a;A1A3数据库服务器处理时间&#xff1a;A2响应时间&#xff1a;N1A1N2A2N3A3N4 负载&#xff1a;模拟业务操作对服务器造成压力的过程&#x…
阅读更多...
shell-函数与数组

shell-函数与数组

1.编写函数&#xff0c;实现打印绿色OK和红色FAILED 判断是否有参数&#xff0c;存在为Ok&#xff0c;不存在为FAILED [rootcotenos day06]# vim colour.sh #!/bin/bash test(){if [ -z $1 ];thenecho -e "\033[31m FAILED \033[0m"elseecho -e "\033[32m …
阅读更多...
git tutorial

git tutorial

最近老板要搞retreat 需要做一个分享&#xff0c;正好把分享的内容作为博客记录一下。 说起git&#xff0c;那就不得不提GitHub。 GitHub 最开始是作为一个面向开源以及私有项目的管理平台。它可以存储代码&#xff0c;文档&#xff0c;数据等等。目前最常用将其作为一个代码…
阅读更多...
中点分割裁剪算法介绍 (简单易懂)

中点分割裁剪算法介绍 (简单易懂)

目录 一、算法介绍 二、算法描述 一、算法介绍 裁剪效果图&#xff1a; 中点分割裁剪算法的思想类似于二分思想&#xff0c;不断地在中点处将线段一分为二&#xff0c;对每段线段重复Cohen-Sutherland裁剪算法的线段可见性测试方法&#xff0c;直至找到每段线段与窗口边界线的…
阅读更多...
STM32MP157驱动开发——Linux块设备驱动

STM32MP157驱动开发——Linux块设备驱动

STM32MP157驱动开发——Linux块设备驱动一、简介二、驱动开发1.使用请求队列的方式2.测试①3.不使用请求队列的方式4.测试②参考文章&#xff1a;【正点原子】I.MX6U嵌入式Linux驱动开发——Linux 块设备驱动 一、简介 之前学习的都是关于字符设备的驱动&#xff0c;包括 plat…
阅读更多...
Node.js下载安装与基础操作

Node.js下载安装与基础操作

&#x1f973;博 主&#xff1a;初映CY的前说 &#x1f31e;个人信条&#xff1a;想要变成得到&#xff0c;中间还有做到&#xff01; &#x1f918;本文核心&#xff1a;Node.js的下载安装操作 node.js下载安装 node.js中文网下载链接http://nodejs.cn/download/ 1.浏…
阅读更多...
模型性能分析：ROC 分析和 AUC

模型性能分析：ROC 分析和 AUC

本文[1]将介绍模型性能分析的两个方法&#xff1a;ROC & AUC。 ROC 分析和曲线下面积 (AUC) 是数据科学中广泛使用的工具&#xff0c;借鉴了信号处理&#xff0c;用于评估不同参数化下模型的质量&#xff0c;或比较两个或多个模型的性能。 传统的性能指标&#xff0c;如准确…
阅读更多...
什么是进程、线程，什么是并发、并行及线程的创建和线程的基本使用

什么是进程、线程，什么是并发、并行及线程的创建和线程的基本使用

一、什么是程序、进程、线程 1、什么是程序 程序可以理解为是我们执行的一段代码&#xff0c;是一种静态的概念 2、什么是进程 进程是指运行中的程序&#xff0c;是一个动态的概念。进程有它自身的产生、存在和消亡的过程&#xff08;进程产生就会占用内存空间&#xff0c;反…
阅读更多...
【WSL】[04]从C盘解放出来WSL的linux镜像

【WSL】[04]从C盘解放出来WSL的linux镜像

前言&#xff1a; C盘的硬盘资源有限&#xff0c;虚拟机的需求无限&#xff0c;所以&#xff0c;要把无限的硬盘需求搞到其他盘去才行啊 方案1&#xff1a;利用工具&#xff1a;move-wsl 1 管理员运行PowerShell,创建WSL的工作目录 移动前&#xff0c;C盘的空间大小&#xf…
阅读更多...
vue-element-表格 Excel 【导出】功能

vue-element-表格 Excel 【导出】功能

表格Excel导出功能 1. 将点击导出按钮添加点击事件click“handleDownload” 并在method中创建方法 <el-button type"danger" size"small" click"handleDownload">excel导出</el-button>复制下面的方法 or 去vue-element-admin中的s…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023