目录

一、算法介绍

二、算法描述

---

一、算法介绍

  裁剪效果图：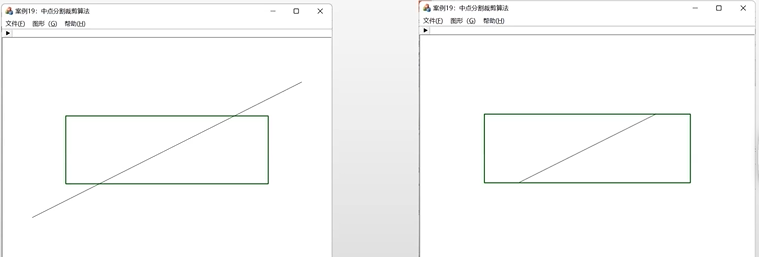

  中点分割裁剪算法的思想类似于二分思想，不断地在中点处将线段一分为二，对每段线段重复Cohen-Sutherland裁剪算法的线段可见性测试方法，直至找到每段线段与窗口边界线的交点或分割子段的长度充分小可视为一点为止。 

  前置知识：Cohen-Sutherland裁剪算法

二、算法描述

  算法步骤有五步，以一个裁剪样例来演示下算法过程：

  比如我们需要将线段 P1P0 进行裁剪。

 

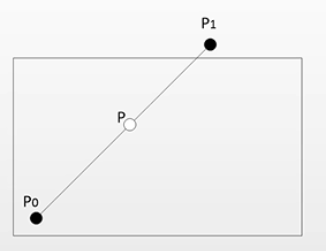
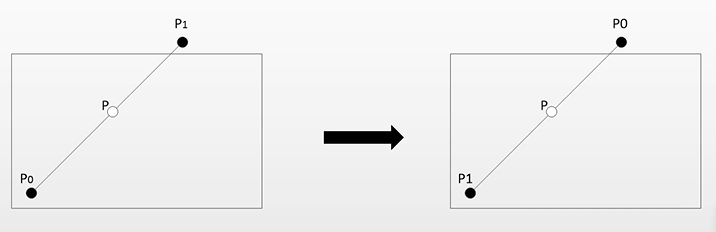
① 如果P1点位于裁剪多边形外部，我们调换P1点和P0点的位置，否则不变。

调换原因：程序始终对p0点进行操作(始终是因为，算法过程中只需要计算出p0点的编码，无需把p1和p0的编码都算出)。由于点位于窗口外时，要进行裁剪操作，所以需交换p1p0点，确保把p0放置在窗口外，这样程序就能一直对p0进行操作了。简单来说，p0点就是用来操作的，所以把p0搞外面去才能一直对p0操作。

② 将端点p1保存到暂存器里。

③ 用中点公式求出线段p1p0的中点P，中点公式如下：

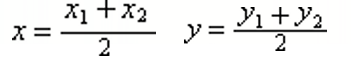
④ 对p0点和中点P进行编码(如何编码请参考Cohen-Sutherland算法)，分别得到C0和C，然后做如下判断(判断原理也请参考Cohen-Sutherland算法，这里不再赘述)：

if((C1&C)!=0)　P0=P;    //端点P0移动到中点P处
Else P1=P;   //否则，移动端点P1到中点P处

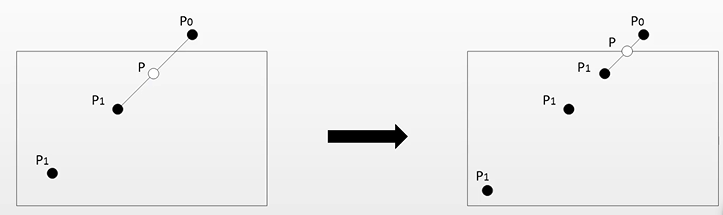
⑤ 回到第③步并继续执行，一直到中点位于裁剪多边形边界上为止(即线段P0P小于某一极小值为止，极值可以取10的负6次方之类)。然后取出暂存器的端点赋给P1，最终得到P1点和P0点，连接即可得到裁剪之后的直线段