经过前面对RRT的介绍，我们发现基于采样的规划算法与基于图搜索的规划算法都是通过对路径树进行拓展新节点，来找到起点到终点的路径解。RRT家族通过随机采样来生成这棵路径树，随机采样会面临采样低效的问题——大部分采样的新节点都无益于提升路径解的最优性。动态规划基于特定规划问题的结构，通过固定的采样得到众多节点，将多阶段的规划问题转变成一系列单阶段最优化问题。同样的规划问题，若能用动态规划来求解，那么动态规划方法的效率比RRT算法要高很多。

一、动态规划：复杂问题简单化

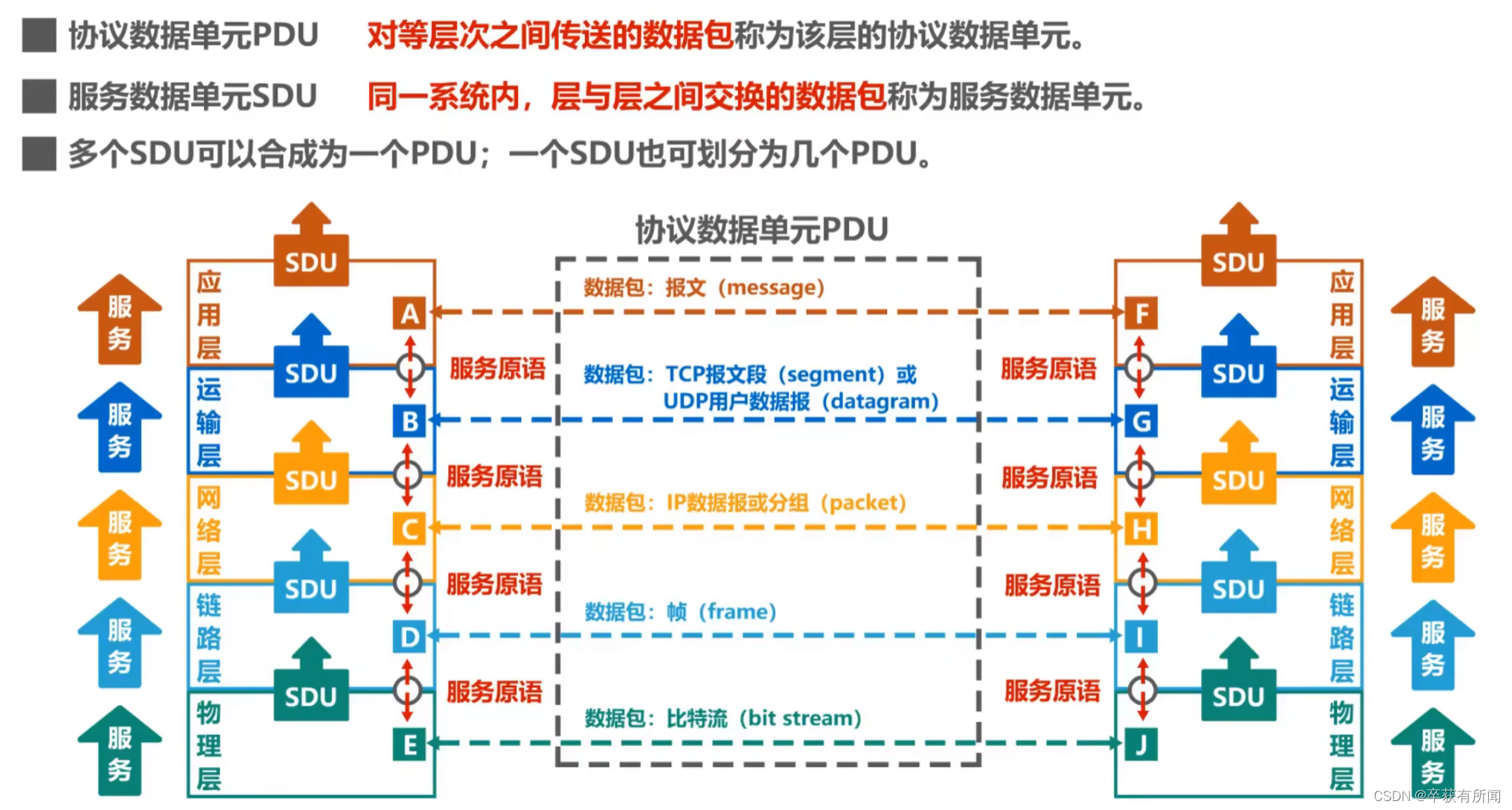
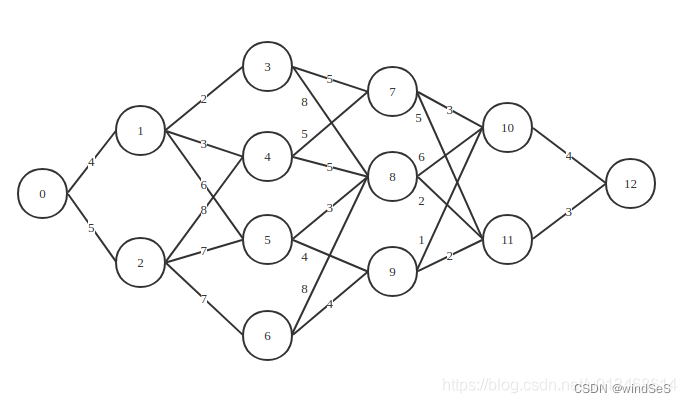
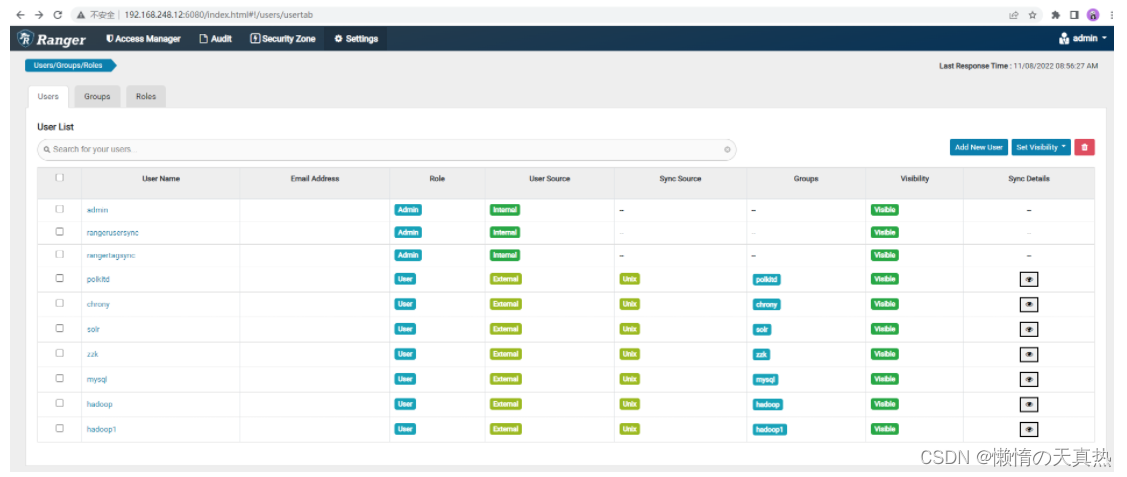
在pygraph实现graph图结构+Dijkstra最短路径（python库）中，给出的例子如下所示。这个图的最短路径问题可以用图搜索方法解决，也可以用动态规划方法解决。

动态规划通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。但是，不是所有的原问题划分成子问题都能用动态规划方法来求解，分解后的子问题必须满足以下两个条件：
1）最优子结构（最优化原理）。可以从子问题的最优解推出原问题的最优解。
2）无后效性。即，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它后续的决策。例如，马尔可夫决策过程就是无后效性的。

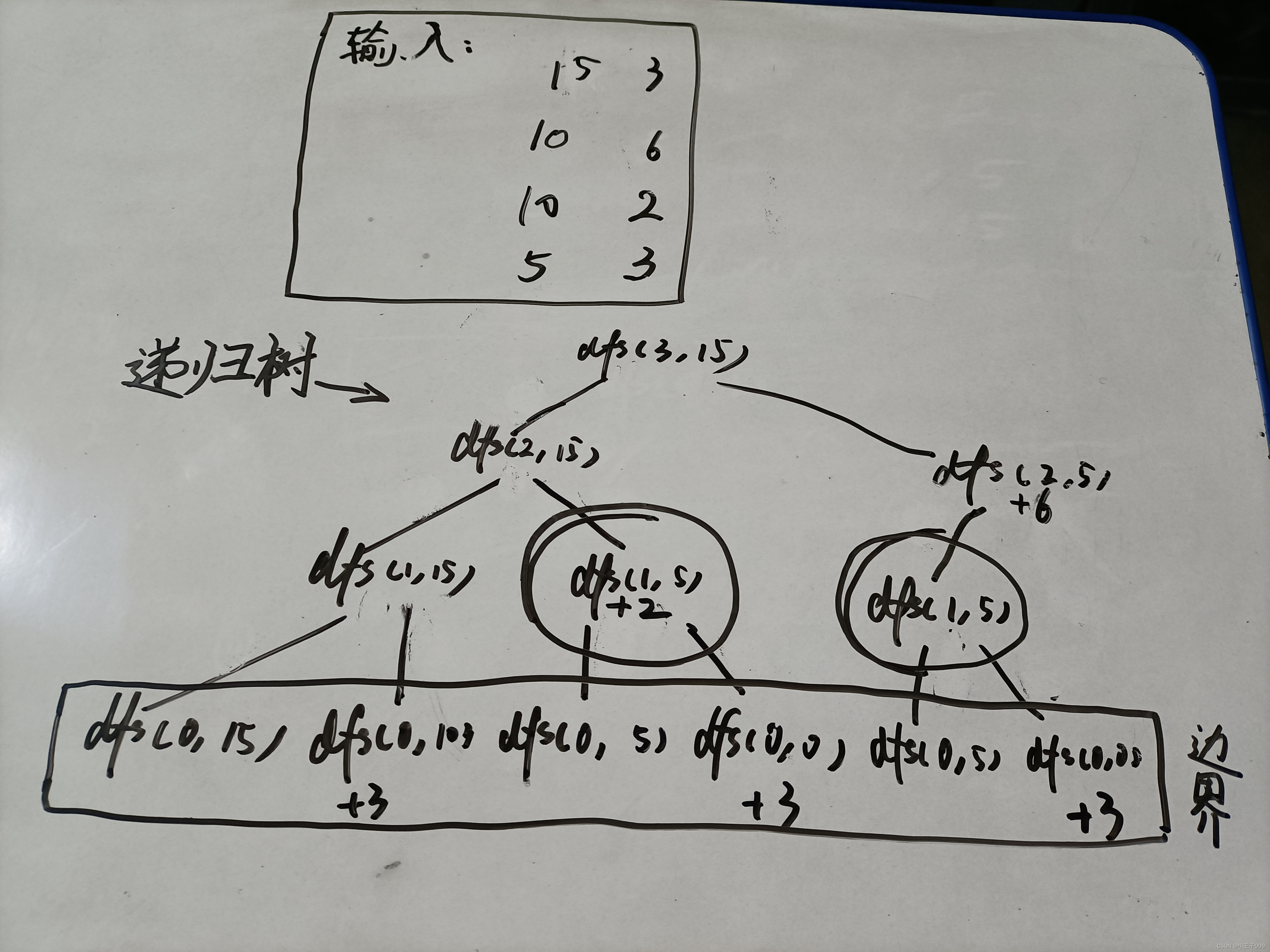
如果一个复杂的多步决策问题可以写成如下所示的贝尔曼方