信号与线性系统翻转课堂笔记17——z变换及其性质
The Flipped Classroom17 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1)序列的z变换的定义,单边和双边z变换;
(2,重点)双边z变换的收敛域;
(3,重点)常用右边、左边、双边序列的z变换:单位序列δ(k)、阶跃序列ε(k)、指数序列a^k、正弦/余弦序列cos( ω_0 k)等;
(4,重点)z变换的性质。
二、问题与解答
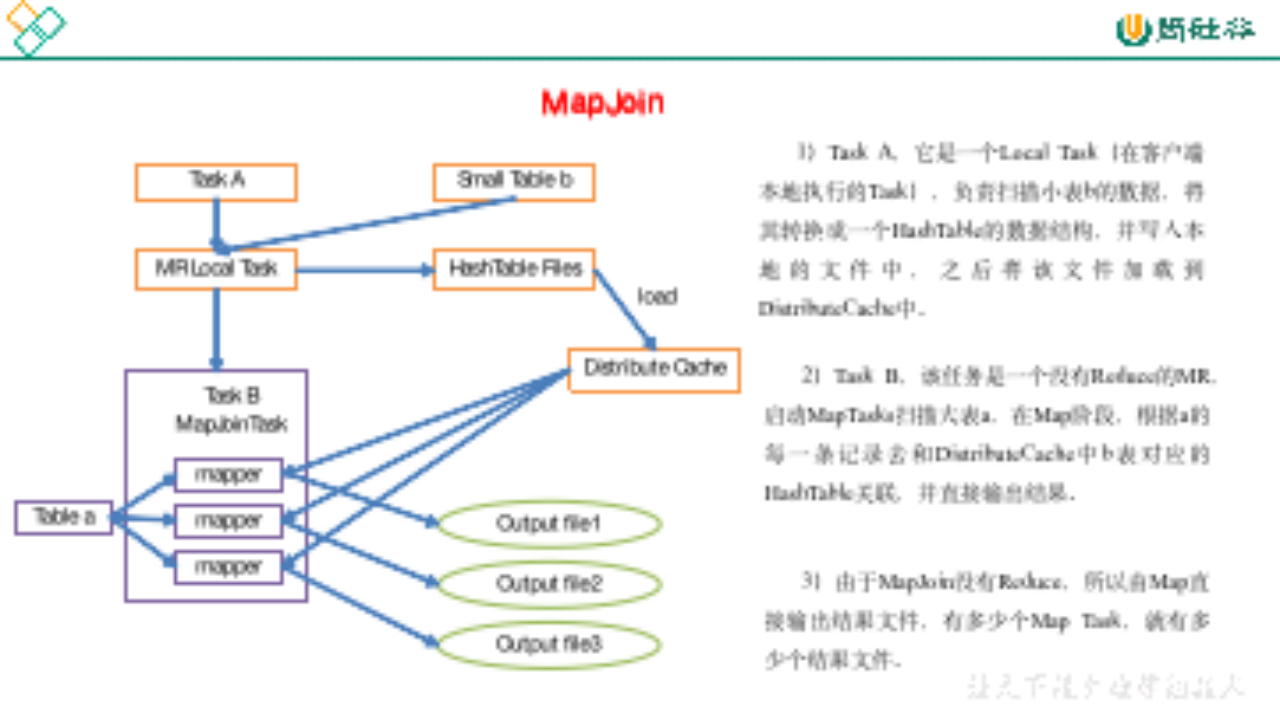
(*1)单边和双边z变换的定义有何区别?为什么对于拉普拉斯变换,一般只考虑单边的,但对于z变换,却需要同时考察双边和单边z变换?这两种z变换的应用场合有什么不同?分别求序列f_1 (k)=0.5^k ε(k)、f_2 (k)=-0.5^k ε(-k-1)的双边z变换。基于结果讨论:对于双边z变换,为什么必须要同时给出z变换表达式和收敛域?
(*2)总结有限长序列、右边序列、左边序列、双边序列各自收敛域的特点(可以举例说明)。序列的起点或者终点,在k=0之前或者之后,对于收敛域会有什么影响?
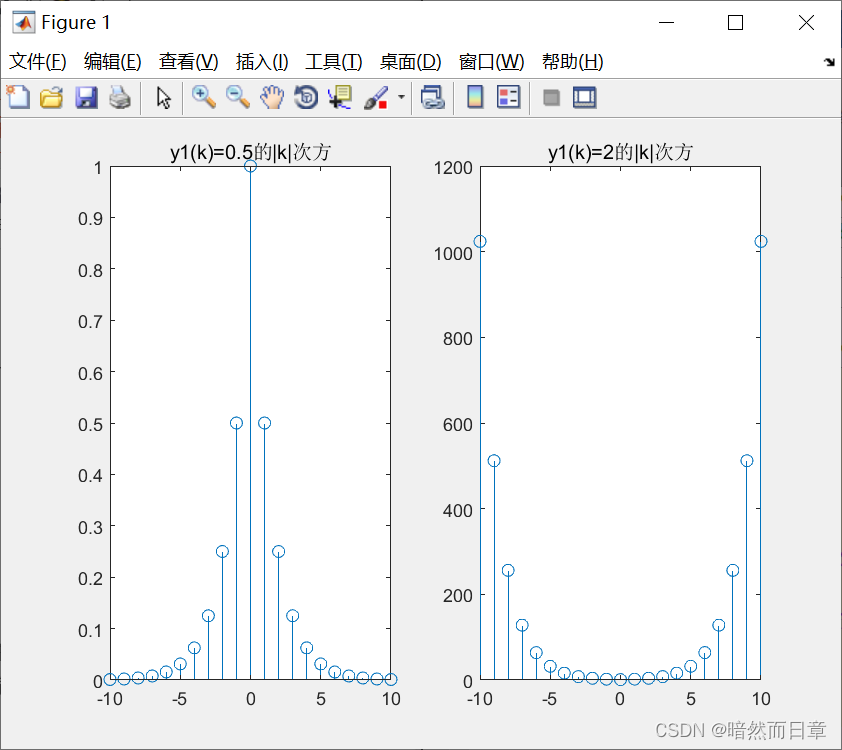
(3)双边序列的z变换是否一定存在?设有两个双边序列:f_1 (k)=0.5^|k| 、f_2 (k)=2^|k| ,用MATLAB分别画出这两个序列的波形(绘图范围|k|≤10),并考察这两个序列的z变换,讨论其z变换的存在性与序列特点之间的关系。
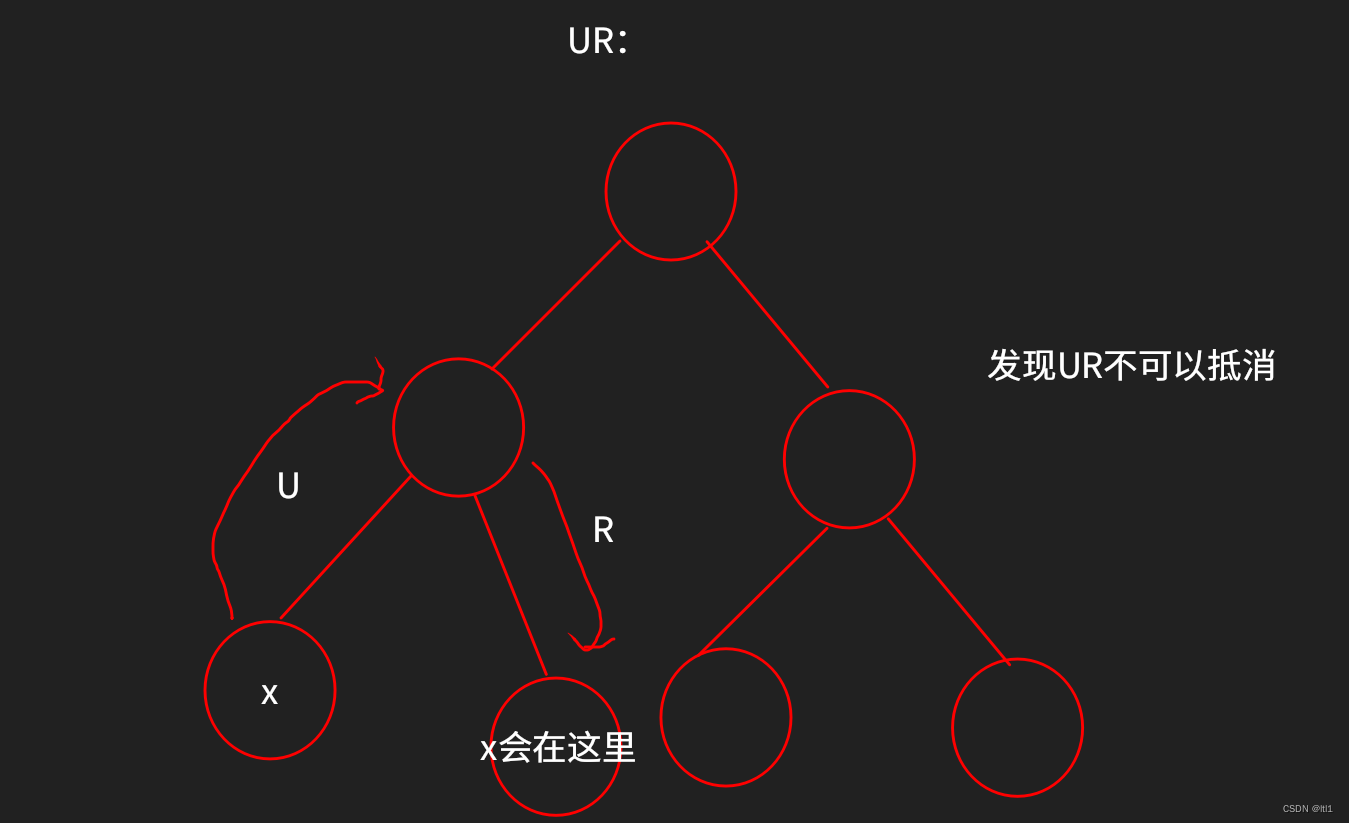
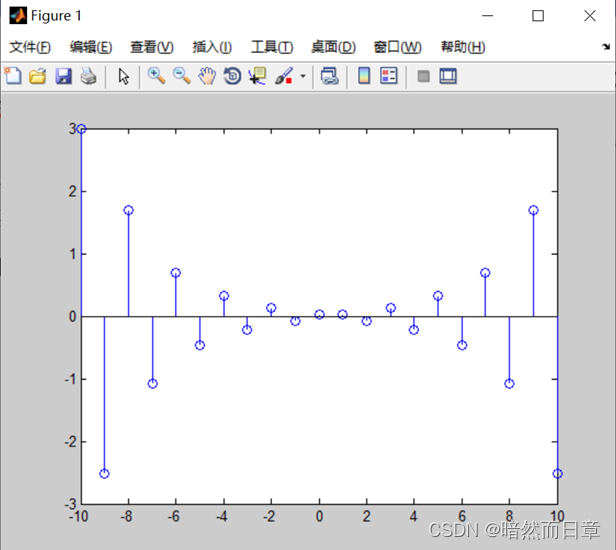
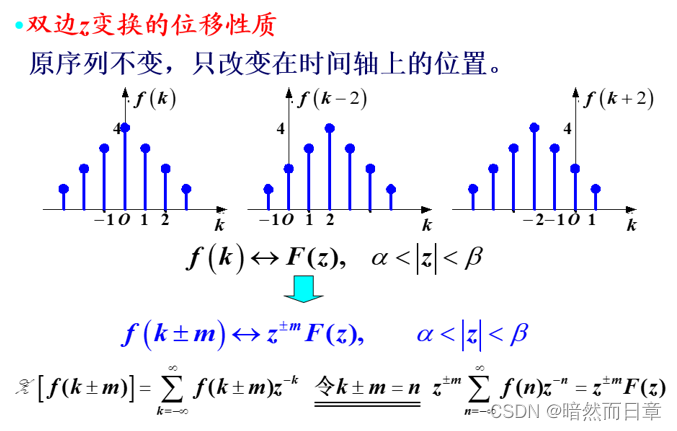
(*4)比较双边和单边z变换的移位(移序)特性有何不同,并分析它们之间为什么会有这样一个区别。请针对如图1所示序列进行分析和讨论。当移位序列和移位方式满足何种条件时,双边和单边z变换的移位特性是相同的?
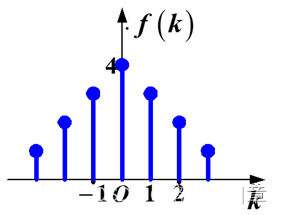
图1
(5)利用z变换的初值定理求序列的初值,是否一定是从k=0开始递推求解?考察信号f(k)=0.5^k ε(k+1),求其双边z变换,用初值定理求解,并与序列在相应点的值进行比较。
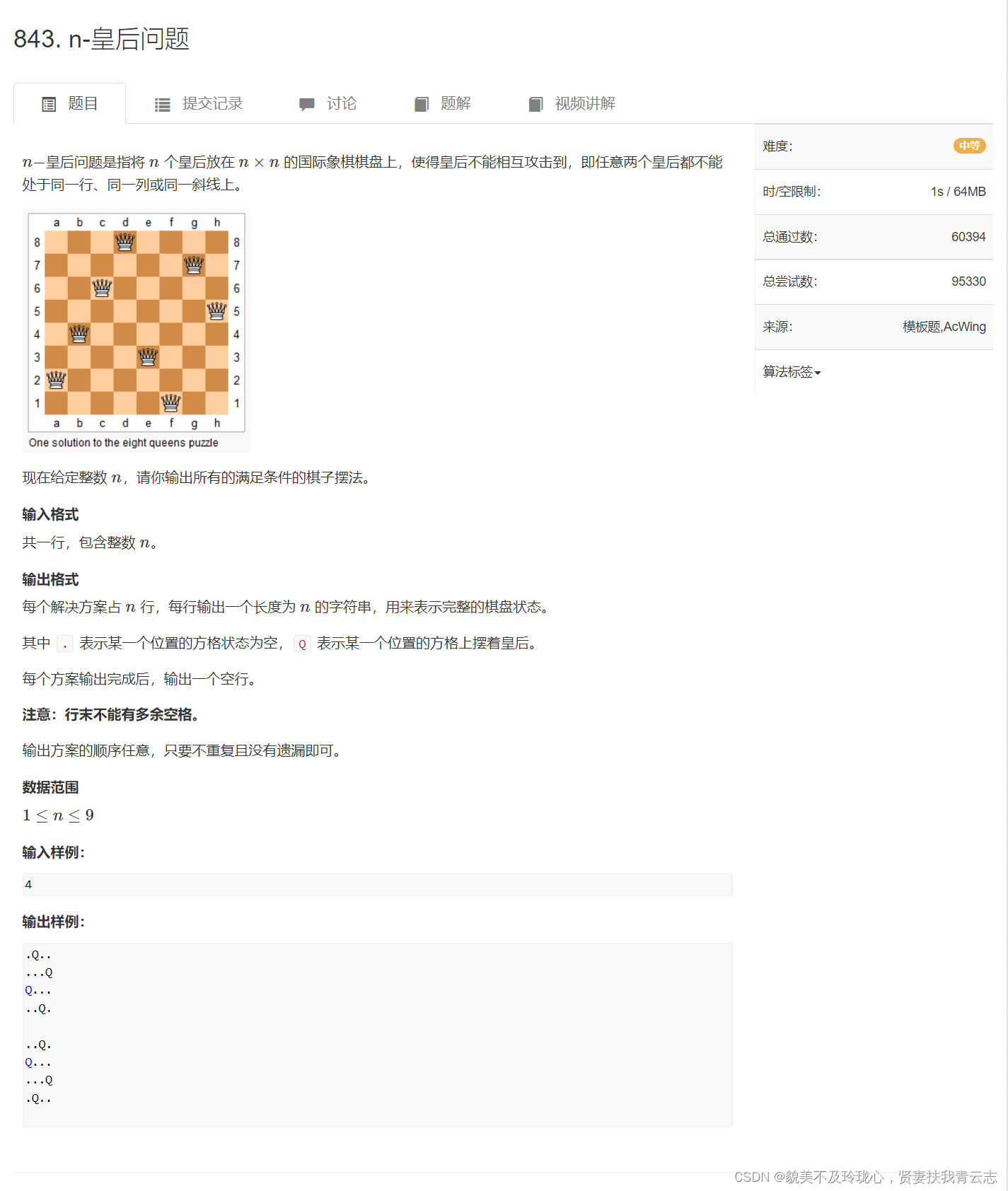
(*6)求解习题6.8,总结序列终值的各种不同情形(等于0、等于常数、不存在等)与z变换形式(极点的分布特点)的关系。

1、单边与双边z变换
单边和双边z变换的定义有何区别?为什么对于拉普拉斯变换,一般只考虑单边的,但对于z变换,却需要同时考察双边和单边z变换?这两种z变换的应用场合有什么不同?分别求序列f_1 (k)=0.5^k ε(k)、f_2 (k)=-0.5^k ε(-k-1)的双边z变换。基于结果讨论:对于双边z变换,为什么必须要同时给出z变换表达式和收敛域?
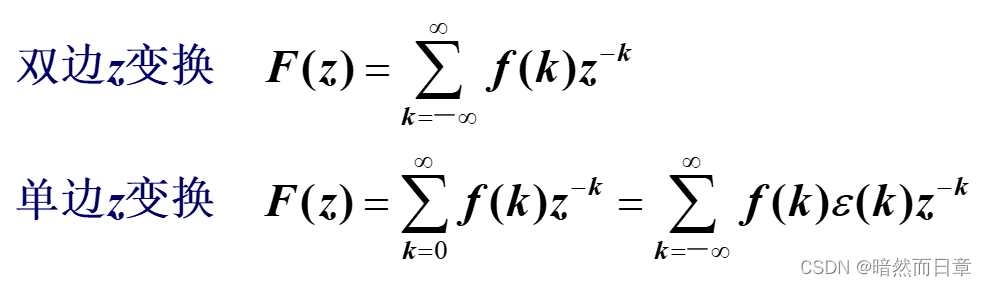
单边拉普拉斯变换是因果系统中的拉普拉斯变换,要考虑初始状态;双边拉普拉斯没有特定条件,是普遍情况。
对于z变换,只有在k<0是f(k)=0的有始序列,单边和双边的z变换相等;否则,两者不一样。



2、收敛域
总结有限长序列、右边序列、左边序列、双边序列各自收敛域的特点(可以举例说明)。序列的起点或者终点,在k=0之前或者之后,对于收敛域会有什么影响?


有限长序列
a、如果k2>k1>=0或k2>=k1>0,收敛区为0<|z|≤∞;
b、如果k2>0,k1<0, 收敛区为0<|z|<∞;
c、如果0≥k2>k1或0>k2≥k1,收敛区为0≤|z|<∞;
d、如果k1=k2=0,收敛区为0≤|z|≤∞。
右边序列
如前所述 ,级数收敛还必须要求其每一项都存在且有限。与有限长序列时的情况一样,这里也可以得出,当k1<0时,|z|不能等于无穷大,收敛区间不包含无穷远点,这时候的收敛区为Rr<|z|<∞。如果k1≥0,则不必要排除无穷远点,收敛区为Rr<|z|≤∞
左边序列、双边序列
在上面的讨论中,左右边序列是根据序列是否有始或有终来定义的,但并没有规定序列的起点或终点的位置。在实际应用中,一般以k=0为分界线,认为右边序列从k=0开始,而左边序列终止于k=-1。后面的内容中如果没有特别说明,所提及的左右序列都遵从这不规定。
3、双边序列z变换的MATLAB实现
双边序列的z变换是否一定存在?设有两个双边序列:f_1 (k)=0.5^|k| 、f_2 (k)=2^|k| ,用MATLAB分别画出这两个序列的波形(绘图范围|k|≤10),并考察这两个序列的z变换,讨论其z变换的存在性与序列特点之间的关系。
k=-10:1:10;
y1=0.5.^abs(k);
k=-10:1:10;
y2=2.^abs(k);
subplot(1,2,1)
stem(k,y1);title('y1(k)=0.5的|k|次方')
subplot(1,2,2)
stem(k,y2);title('y1(k)=2的|k|次方')
f_1 (k)=0.5^|k|的z变换(仅供参考)
f_2 (k)=2^|k| 没有z变换
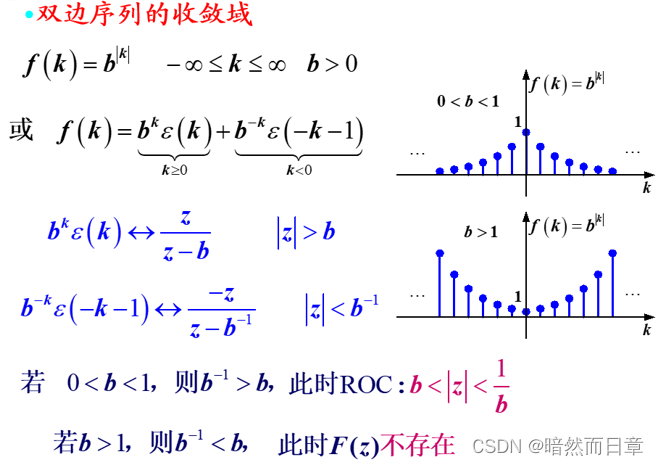
当k趋近于无穷时,序列波形趋近于0,此时,收敛域存在,反之,不存在。
4、双边和单边z变换的位移性质
比较双边和单边z变换的移位(移序)特性有何不同,并分析它们之间为什么会有这样一个区别。请针对如图1所示序列进行分析和讨论。当移位序列和移位方式满足何种条件时,双边和单边z变换的移位特性是相同的?

图1
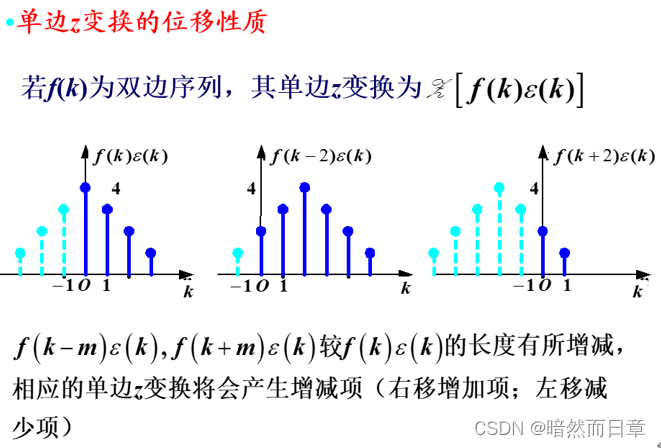


5、利用z变换初值定理求初值
利用z变换的初值定理求序列的初值,是否一定是从k=0开始递推求解?考察信号f(k)=0.5^k ε(k+1),求其双边z变换,用初值定理求解,并与序列在相应点的值进行比较。
(1)不一定



6、终值定理不同情形与z变换形式
求解习题6.8,总结序列终值的各种不同情形(等于0、等于常数、不存在等)与z变换形式(极点的分布特点)的关系。



三、反思总结
暂无