目录
DFS
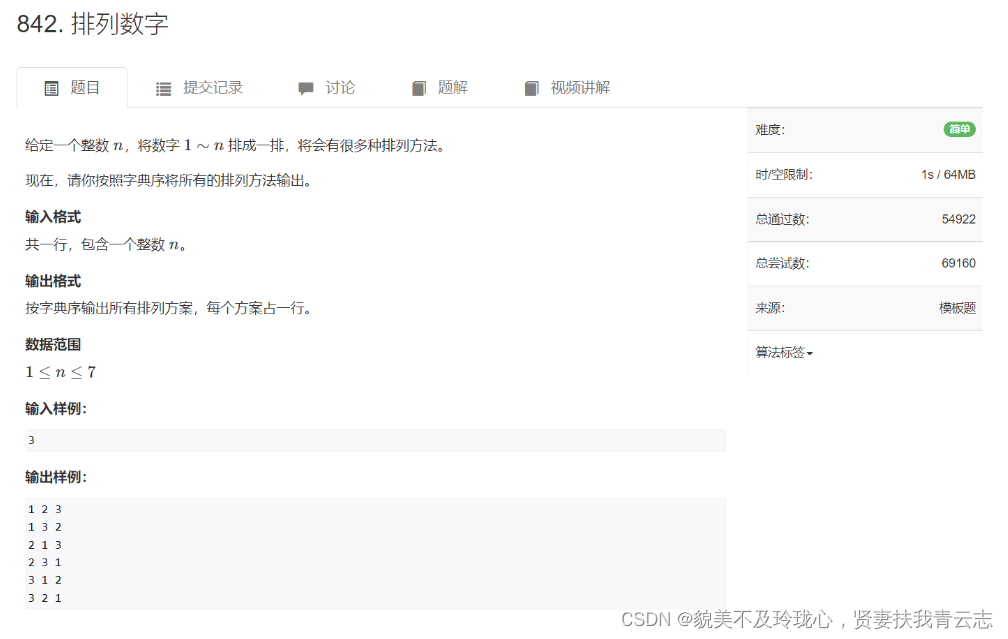
实现数字全排列
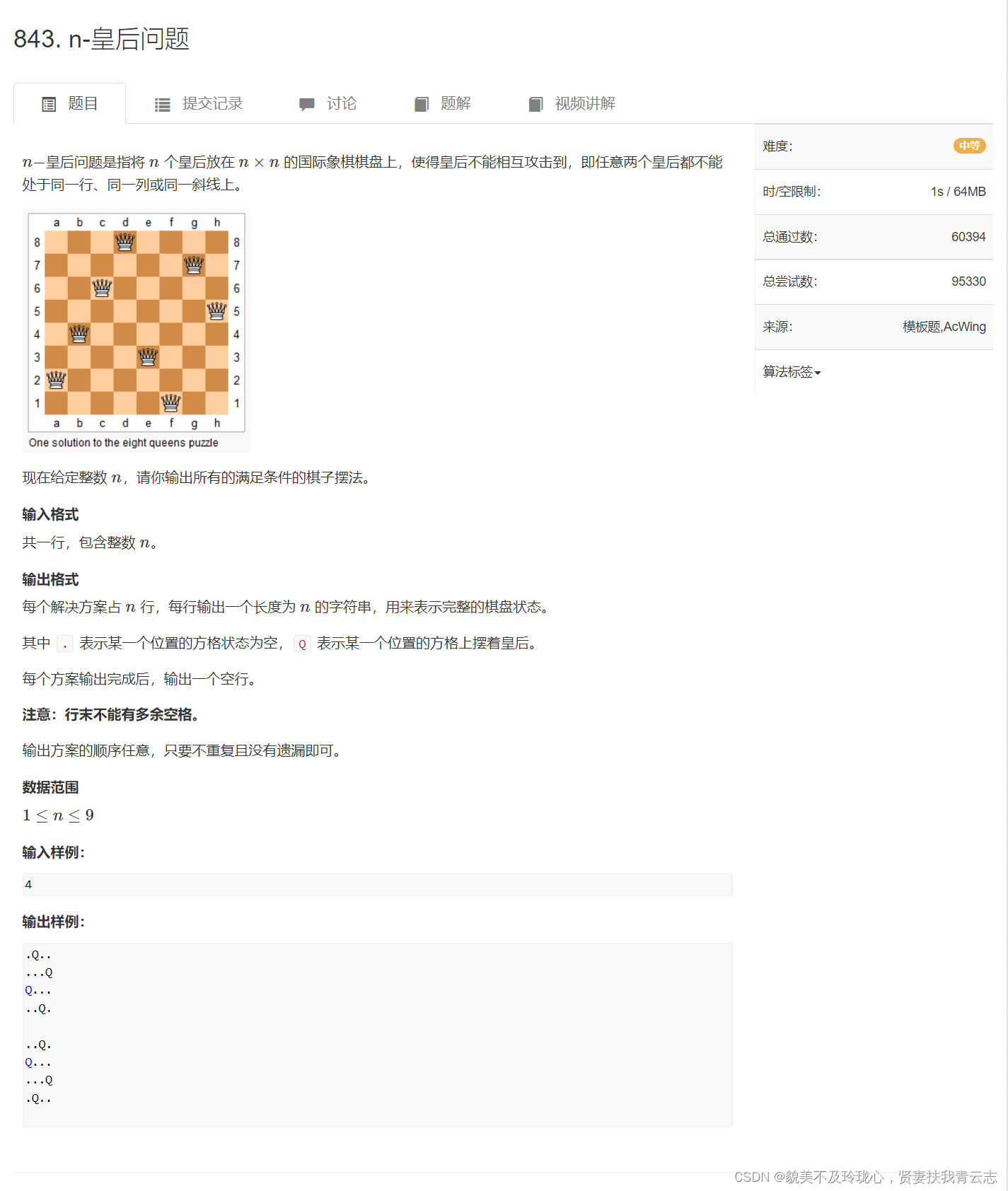
N 皇后问题
DFS
算法的理解
-
优先考虑深度,换句话说就是一条路走到黑,直到无路可走的情况下,才会选择回头,然后重新选择一条路。空间复杂度:O(h)和高度成正比
-
不具有最短路性
DFS板子
DFS没有固定的代码板子,只有一个思路
如下所示:
check函数可以用布尔数组代替,达到优化的目的
int check(参数)
{
if(满足条件)
return 1;
return 0;
}
void dfs(int step) //step表示深度搜索的深度增加,也就是图中节点
{
处理递归的边界
{
相应操作
}
for循环迭代途中所有元素
{
判断满足check条件
标记状态
继续下一步dfs(step+1)//深度加深
恢复初始状态(回溯的时候要用到)修改为原始状态,通过对每个元素的状态修来来完成回溯的操作。
}
} 实现数字全排列
这道题并不是标准的使用 dfs 算法搜索图中的点,只是因为对每个位置的数字选择符合递归的特点,所以可以使用递归来解决问题。使用一个数据记录遍历一条到底的路径。
#include <iostream>
using namespace std;
const int N=10;
int n;
int a[N];
bool state[N];
void dfs(int u)//u:表示搜索的节点
{
//边界情况处理
if(u>n)
{
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
printf("\n");
}
//一般情况
for(int i=1;i<=n;i++)
{
if(!state[i])
{
state[i]=1;
a[u]=i;
dfs(u+1);//搜索下一个节点
state[i]=0;//状态回溯
}
}
}
int main()
{
cin>>n;
dfs(1);//从根节点开始搜索
return 0;
}N 皇后问题
和数字全排列一样,其中解决问题的思路和dfs很像。
按行回溯, 时间复杂度O(n!)
#include<iostream>
using namespace std;
const int N=20;
int n;
char g[N][N];
bool col[N],dg[N],udg[N];
void dfs(int u)
{
if(u==n)
{
// 等价于cout << g[i] << endl;
for(int i=0;i<n;i++) puts(g[i]);
puts("");
return;
}
for(int i=0;i<n;i++)
{
// 对于斜线,反斜线的标记是利用率映射的思想
// 剪枝(对于不满足要求的点,不再继续往下搜索)
// udg[n - u + i],+n是为了保证下标非负
if(!col[i] && !dg[n-u+i] && !udg[u+i])
{
col[i]=dg[n-u+i]=udg[u+i]=1;
g[u][i]='Q';
dfs(u+1);
col[i]=dg[n-u+i]=udg[u+i]=0;
g[u][i]='.';
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]='.';
dfs(0);
return 0;
}DFS是优先考虑深度搜索,之后再进行回溯。
递归函数负责往深度走,递归函数调用完后,清除标记,for循环起到在每一层遍历的作用
这里的两道dfs问题都是全排列问题,对当前位置的元素选取是需要需要记录与抹除状态。