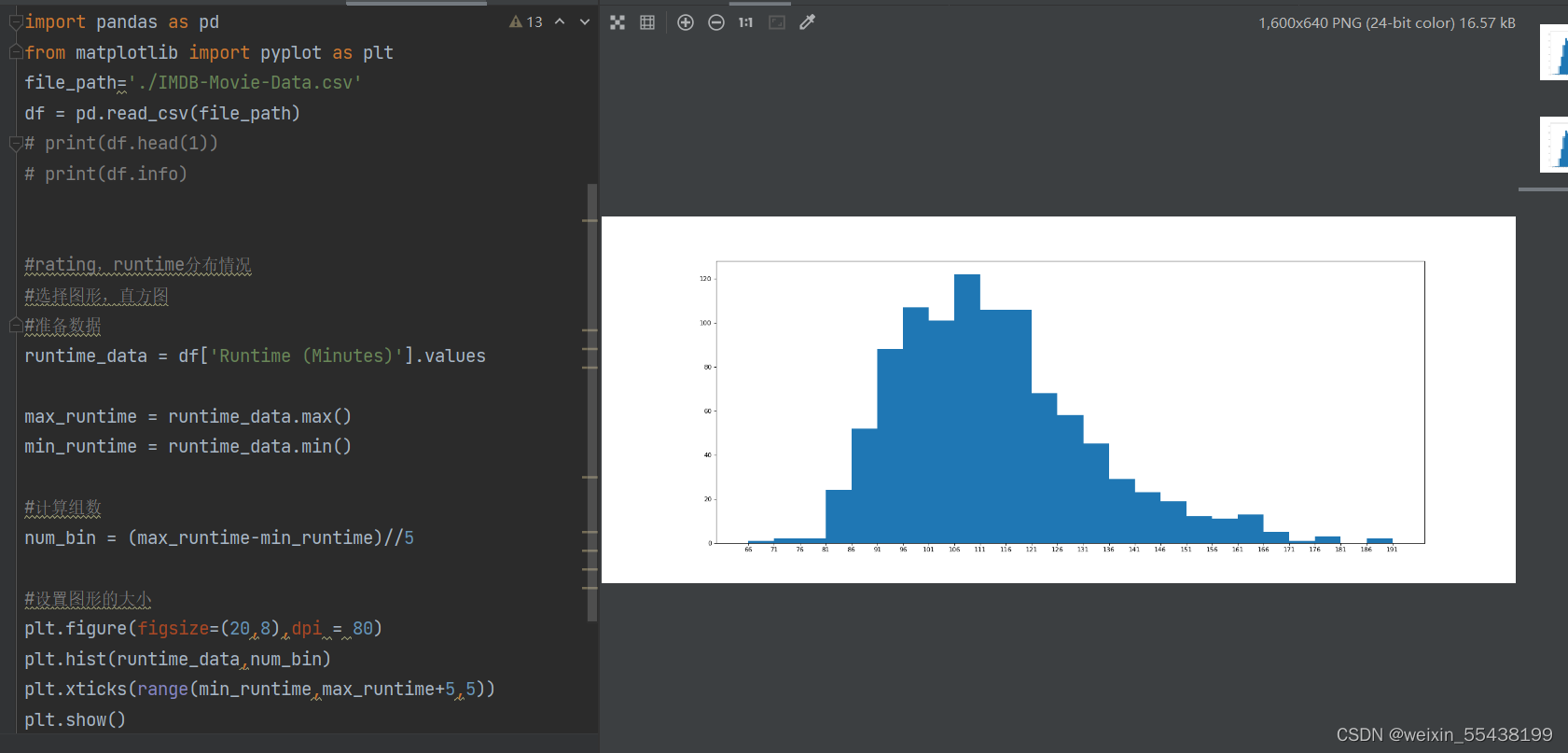
力扣：72. 编辑距离
这道题目让我狠狠的了解了动态规划，这玩意是真强。
题目描述很简单：

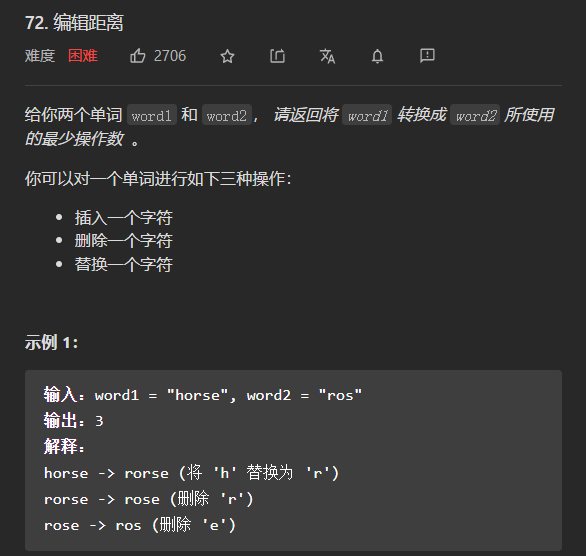
这道题正常来说，我们要考虑这个字符怎么换，长度不一怎么找…等等问题，但是这样做会发现很困难，显然这是行不通的，我们对这个题目进行分析：
首先我们给定两个字符串A=hores,B=ros，假设从A[0,i]到B[0,j]需要的编辑距离为k，那么我们想一下：

• 如果horse到ro的编辑距离为a，那么从horse到ros的编辑距离应该就是a+1，相当于给变化后的A添加一个字母s
• 如果hors到ros的编辑距离为b，那么从horse到ros的编辑距离应该就是b+1,相当于给变化后的B添加一个字母e
• 如果hors到ro的编辑距离为c，那么从horse到ros的编辑距离应该就是c+1，相当于修改变化后的A的一个字母

所以从A变成B的编辑距离应该就是min(a+1,b+1,c+1)

那么我们定义一个dp数组dp[i][j]表示A的前i个字母和B的前j个字母之间的编辑距离，所以就有：

• dp[i][j-1]为A的前i个字符和B的前j-1个字符编辑子距离的问题，根据上面的分析，那么dp[i][j]最小可以为dp[i][j-1]+1

• dp[i-1][j]为A的前i-1个字符和B的前j个字符编辑子距离的问题，根据上面的分析，那么dp[i][j]最小可以为dp[i-1][j]+1

• dp[i-1][j-1]为A的前i-1个字符和B的前j-1个字符编辑子距离的问题，根据上面的分析，那么dp[i][j]最小可以为dp[i-1][j-1]（因为当最后A[i]=B[j]的时候，是可以不用做操做的）
  所以我们的状态转移方程为：

• 当A和B的最后一个字母不同时
  dp[i][j] = 1+min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]);

• 当A和B的最后一个字母相同时：
  dp[i][j] = dp[i-1][j-1]
  所以我们最终的代码为：

  public int minDistance(String word1, String word2) {
        int len = word1.length(),width = word2.length();
        int[][] dp= new int[len+1][width+1];
	//构建str1的dp情况
        for(int i = 0;i<=len;i++){
            dp[i][0] = i;
        }
	//构建str2的dp情况	
        for(int j = 0;j<=width;j++){
            dp[0][j] = j;
        }
        for(int i = 1;i<=len;i++){
            for(int j = 1;j<=width;j++){
		//循环遍历从A[0..i]到B[0..j]的子串的情况
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = 1 + Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]));
                }
            }
        }
        return dp[len][width];
    }