文章目录
- 前言
- 一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化
- 1、观察空间(右手坐标系、透视相机)
- 2、裁剪空间(左手坐标系、且转化为了齐次坐标)
- 3、屏幕空间(把裁剪坐标归一化设置)
- 4、从观察空间到裁剪空间
- 5、从裁剪空间到屏幕空间后
- 二、透视相机的参数推导
- 1、从XoY平面,求出X~v~从观察空间到裁剪空间的坐标投影 X~p~
- 2、从YoZ平面,求出Y~v~从观察空间到裁剪空间的坐标投影 Y~p~
- 三、把投影到近裁剪面的坐标 归一化设置
- 1、求归一化设置后的 x~n~
- 2、求归一化设置后的 y~n~
- 3、得到最后化简的公式
- 四、构建转化矩阵
- 1、在OpenGL[-1,1]下:
- 2、在DirectX[1,0]下:
- 3、把A、B代入矩阵得
前言
我们把顶点坐标信息转化为裁剪空间。有可能使用到正交相机信息 或 透视相机。我们在这篇文章中,推导一下透视相机视图空间下的坐标转化到裁剪空间的矩阵。

一、简单看一下 观察空间—>裁剪空间—>屏幕空间 的转化

1、观察空间(右手坐标系、透视相机)
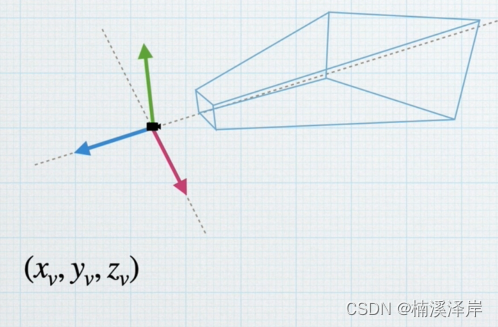
2、裁剪空间(左手坐标系、且转化为了齐次坐标)
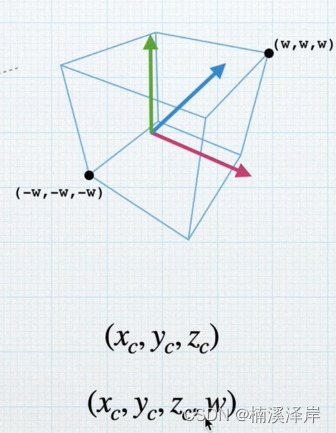
3、屏幕空间(把裁剪坐标归一化设置)

4、从观察空间到裁剪空间
用透视投影矩阵先转化到裁剪空间
然后,在转化为齐次坐标
5、从裁剪空间到屏幕空间后
− 1 ≤ x c w ≤ 1 -1 \leq \frac{x_c}{w}\leq1 −1≤wxc≤1
− w ≤ x c ≤ w -w \leq x_c\leq w −w≤xc≤w
二、透视相机的参数推导
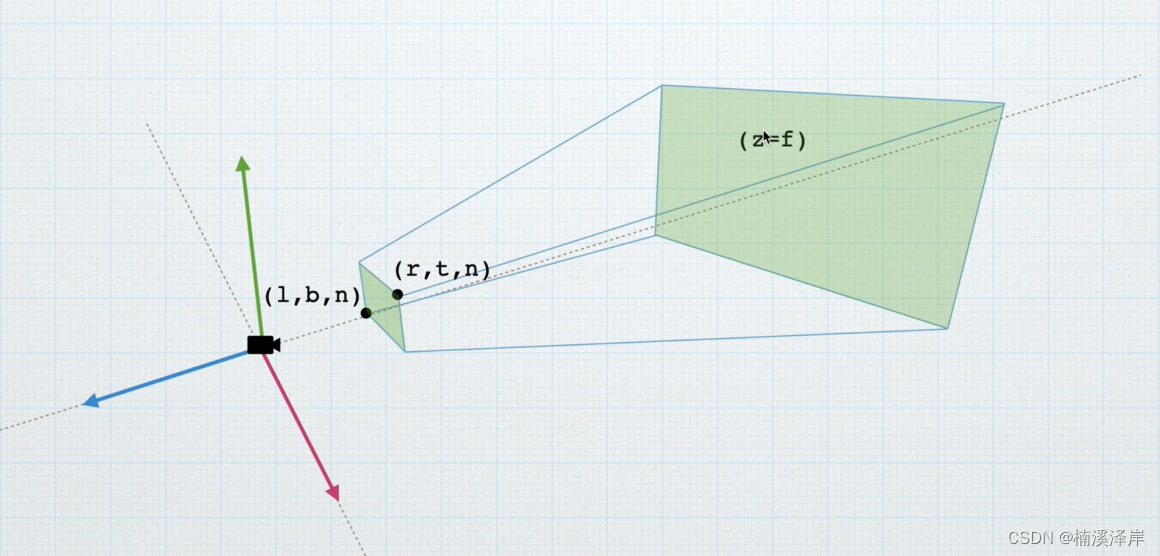
- 我们对于远裁剪面只是已知 f,其他参数都是未知
1、从XoY平面,求出Xv从观察空间到裁剪空间的坐标投影 Xp

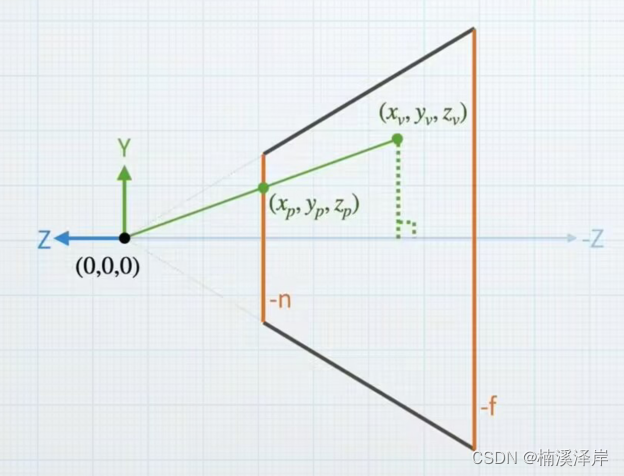
- 点 V 是观察空间下的模型顶点,xyz是已知的
已知: ( x v , y v , z v ) 、 − n (x_v,y_v,z_v) 、 -n (xv,yv,zv)、−n - 点P是该点在近裁剪面上的投影点,xyz是未知的
未知: ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp) - 我们在 XoZ平面上,能求的就是 xp
求: x p x_p xp
z p = − n z_p = -n zp=−n
y p 在 X o Z 平面下,无法计算 y_p 在XoZ平面下,无法计算 yp在XoZ平面下,无法计算
- v点向Z轴做垂线,原点连接v点,围成的两个三角形相似,可得:
x p x v = − n z v \frac{x_p}{x_v} = \frac{-n}{z_v} xvxp=zv−n
x p = − n z v x v x_p = \frac{-n}{z_v} x_v xp=zv−nxv
P = ( − n z v x v , 未知 , − n ) P = (\frac{-n}{z_v}x_v,未知,-n) P=(zv−nxv,未知,−n)
2、从YoZ平面,求出Yv从观察空间到裁剪空间的坐标投影 Yp
- 点 V 是观察空间下的模型顶点,xyz是已知的
已知: ( x v , y v , z v ) 、 − n (x_v,y_v,z_v) 、 -n (xv,yv,zv)、−n - 点P是该点在近裁剪面上的投影点,xyz是未知的
未知: ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp) - 我们在 YoZ平面上,能求的就是 yp
求: y p y_p yp
z p = − n z_p = -n zp=−n
x p 在 X o Z 平面下,无法计算 x_p 在XoZ平面下,无法计算 xp在XoZ平面下,无法计算
- v点向Z轴做垂线,原点连接v点,围成的两个三角形相似,可得:
y p y v = − n z v \frac{y_p}{y_v} = \frac{-n}{z_v} yvyp=zv−n
y p = − n z v y v y_p = \frac{-n}{z_v} y_v yp=zv−nyv
P = ( − n z v x v , − n z v y v , − n ) P = (\frac{-n}{z_v}x_v,\frac{-n}{z_v} y_v,-n) P=(zv−nxv,zv−nyv,−n)
三、把投影到近裁剪面的坐标 归一化设置
P = ( − n z v x v , − n z v y v , − n ) P = (\frac{-n}{z_v}x_v,\frac{-n}{z_v} y_v,-n) P=(zv−nxv,zv−nyv,−n)
化到[-1,1]之间
具体参考Unity中Shader裁剪空间推导(正交相机到裁剪空间的转化矩阵)
1、求归一化设置后的 xn
- l ≤ x ≤ r l \leq x \leq r l≤x≤r 化为: − 1 ≤ 2 x w ≤ 1 -1 \leq \frac{2x}{w} \leq 1 −1≤w2x≤1
− 1 ≤ − 2 n x v z v w ≤ 1 -1\leq \frac{-2nx_v}{z_vw}\leq 1 −1≤zvw−2nxv≤1
− 1 ≤ − 2 n w ⋅ x v z v ≤ 1 -1\leq \frac{-2n}{w}·\frac{x_v}{z_v}\leq 1 −1≤w−2n⋅zvxv≤1
2、求归一化设置后的 yn
- l ≤ y ≤ r l \leq y \leq r l≤y≤r 化为: − 1 ≤ 2 y h ≤ 1 -1 \leq \frac{2y}{h} \leq 1 −1≤h2y≤1
− 1 ≤ − 2 n y v z v h ≤ 1 -1\leq\frac{-2ny_v}{z_vh}\leq1 −1≤zvh−2nyv≤1
− 1 ≤ − 2 n h ⋅ y v z v ≤ 1 -1\leq\frac{-2n}{h}·\frac{y_v}{z_v}\leq1 −1≤h−2n⋅zvyv≤1
3、得到最后化简的公式
由于NDC下的坐标由透视除法而得
我们假设透视除法中的 w 为 -zv
还原到裁剪空间还需要乘以 -zv
- X:
− 1 ≤ − 2 n w ⋅ x v z v ≤ 1 -1\leq \frac{-2n}{w}·\frac{x_v}{z_v}\leq 1 −1≤w−2n⋅zvxv≤1
x n = − 2 n w x v z v x_n = \frac{-2n}{w}\frac{x_v}{z_v} xn=w−2nzvxv
− x n z v = 2 n w x v -x_nz_v = \frac{2n}{w}x_v −xnzv=w2nxv
- Y:
− 1 ≤ − 2 n h ⋅ y v z v ≤ 1 -1\leq\frac{-2n}{h}·\frac{y_v}{z_v}\leq1 −1≤h−2n⋅zvyv≤1
y n = − 2 n h y v z v y_n = \frac{-2n}{h}\frac{y_v}{z_v} yn=h−2nzvyv
− y n z v = 2 n h y v -y_n z_v= \frac{2n}{h}y_v −ynzv=h2nyv
- Z:
z n = ? z_n = ? zn=?
− z n z v = − z v ? -z_nz_v = -z_v? −znzv=−zv?
- W:
w = 1 w = 1 w=1
− w n z v = − z v -w_nz_v = -z_v −wnzv=−zv
四、构建转化矩阵
裁剪空间下的点 = 观察空间下的基向量 在 裁剪空间下的矩阵 * 点在观察空间下的坐标
P c = [ V c ] ⋅ P v P_c = [V_c]·P_v Pc=[Vc]⋅Pv
P c = [ C v ] − 1 ⋅ P v P_c = [C_v]^{-1}·P_v Pc=[Cv]−1⋅Pv
P c = [ C v ] T ⋅ P v P_c = [C_v]^{T}·P_v Pc=[Cv]T⋅Pv
- − x n z v = 2 n w x v -x_nz_v = \frac{2n}{w}x_v −xnzv=w2nxv
- − y n z v = 2 n h y v -y_n z_v= \frac{2n}{h}y_v −ynzv=h2nyv
- − z n z v = − z v ? -z_nz_v = -z_v? −znzv=−zv?
- − w n z v = − z v -w_nz_v = -z_v −wnzv=−zv
[ 2 v w 0 ? ? 0 2 n h ? ? 0 0 ? ? 0 0 ? ? ] T = [ 2 v w 0 0 0 0 2 n h 0 0 ? ? ? ? ? ? ? ? ] \begin{bmatrix} \frac{2v}{w} & 0 & ? &?\\ 0 & \frac{2n}{h} & ? &?\\ 0 & 0 & ? &?\\ 0 & 0 & ? & ?\\ \end{bmatrix}^T =\begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ ? & ? & ? &?\\ ? & ? & ? & ?\\ \end{bmatrix} w2v0000h2n00???????? T= w2v0??0h2n??00??00??
[ 2 v w 0 0 0 0 2 n h 0 0 ? ? ? ? ? ? ? ? ] ⋅ [ x v y v z v 1 ] = ( − x n z v , − y n z v , − z n z v , − w n z v ) \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ ? & ? & ? &?\\ ? & ? & ? & ?\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix} = (-x_nz_v,-y_nz_v,-z_nz_v,-w_nz_v) w2v0??0h2n??00??00?? ⋅ xvyvzv1 =(−xnzv,−ynzv,−znzv,−wnzv)
最后一行由于相乘结果为1可以得出,把最后未知部分设为A,B
[
2
v
w
0
0
0
0
2
n
h
0
0
0
0
A
B
0
0
−
1
0
]
⋅
[
x
v
y
v
z
v
1
]
\begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & A &B\\ 0 & 0 & -1 & 0\\ \end{bmatrix} · \begin{bmatrix} x_v\\ y_v\\ z_v\\ 1\\ \end{bmatrix}
w2v0000h2n0000A−100B0
⋅
xvyvzv1
z c = A z v + B z_c = Az_v+B zc=Azv+B
− z n z v = − z v -z_nz_v = -z_v −znzv=−zv
z c − z v = A z v + B − z v \frac{z_c}{-z_v} = \frac{Az_v+B}{-z_v} −zvzc=−zvAzv+B
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
1、在OpenGL[-1,1]下:
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
{ z v = − n , z n = − 1 z v = − f , z n = 1 \begin{cases} z_v = -n,z_n=-1 \\ z_v = -f,z_n = 1 \end{cases} {zv=−n,zn=−1zv=−f,zn=1
{ − 1 = − A n + B n 1 = − A f + B f \begin{cases} -1 = \frac{-An+B}{n}\\ 1 = \frac{-Af + B}{f} \end{cases} {−1=n−An+B1=f−Af+B
{ − n = − A n + B f = − A f + B \begin{cases} -n = -An+B\\ f = -Af + B \end{cases} {−n=−An+Bf=−Af+B
B = A n − n B = An - n B=An−n
f = − A f + A n − n f = -Af +An-n f=−Af+An−n
f + n = A ( n − f ) f + n= A(n-f) f+n=A(n−f)
A = n + f n − f A = \frac{n+f}{n-f} A=n−fn+f
B = n + f n − f n − n B = \frac{n+f}{n-f}n-n B=n−fn+fn−n
B = n 2 + f n n − f n 2 − n f n − f B = \frac{n^2 + fn}{n-f}\frac{n^2-nf}{n-f} B=n−fn2+fnn−fn2−nf
B = 2 n f n − f B = \frac{2nf}{n-f} B=n−f2nf
2、在DirectX[1,0]下:
z n = A z v + B − z v z_n = \frac{Az_v+B}{-z_v} zn=−zvAzv+B
{ z v = − n , z n = 1 z v = − f , z n = 0 \begin{cases} z_v = -n,z_n=1 \\ z_v = -f,z_n = 0 \end{cases} {zv=−n,zn=1zv=−f,zn=0
{ 1 = − A n + B n 0 = − A f + B f \begin{cases} 1 = \frac{-An+B}{n}\\ 0 = \frac{-Af+B}{f} \end{cases} {1=n−An+B0=f−Af+B
{ n = − A n + B 0 = − A f + B \begin{cases} n = -An+B\\ 0 = -Af+B \end{cases} {n=−An+B0=−Af+B
B = A f B = Af B=Af
n = − A n + A f n = -An+Af n=−An+Af
n = A ( f − n ) n = A(f-n) n=A(f−n)
A = n f − n A =\frac{n}{f-n} A=f−nn
B = n f f − n B = \frac{nf}{f-n} B=f−nnf
3、把A、B代入矩阵得
- OpenGL
[ 2 v w 0 0 0 0 2 n h 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2v0000h2n0000n−fn+f−100n−f2nf0 - DirectX
[ 2 v w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2v}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2v0000h2n0000f−nn−100f−nnf0