目录
一. 泊松分布
1.1 理论部分
1.2 MATLAB函数模型
1.3 例题
二. 正态分布
2.1 理论部分
2.2 MATLAB函数模型
2.3 例题
三. 伽玛分布
3.1 理论部分
3.2 MATLAB函数模型
3.3 例题
一. 泊松分布
1.1 理论部分
Poisson分布是离散的,其x值只能取自然数。Poisson分布的概率密度函数如下:
其中是一个固定的正整数常数。在泊松分布中,参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。以下情况可以构建泊松分布模型:
- 某一服务设施在一定时间内到达的人数
- 电话交换机接到呼叫的次数
- 汽车站台的候客人数
- 机器出现的故障数
- 自然灾害发生的次数
1.2 MATLAB函数模型
泊松分布的概率密度函数,在MATLAB中可以直接调用:
y=poisspdf(x,lambda);
%给定x与lambda的值,就可以直接求该点的概率密度值分布函数(累积概率函数),在MATLAB中可以直接调用:
F=poisscdf(x,lambda)如果给定分布函数值,反过来求x,则需要调用逆概率分布函数:
x=poissinv(F,lambda)MATLAB本身非常适合用来处理向量和矩阵,所以,如果输入的x为一个向量的话,那么输出的y则是x各个点处的概率密度函数值。
1.3 例题
绘制时,泊松分布的概率密度函数与概率分布函数曲线图。
MATLAB代码:
x=[0:15]';
%x为0~15之间的整数,注意需要通过'转为列向量
y1=[]; y2=[];
%要画两个图像
lam1=[1,2,5,10];
%lambda确定了,泊松分布就确定了
for i=1:length(lam1) %lam1的长度为4
y1=[y1,poisspdf(x,lam1(i))]; %lam1(i)代表调用集合lam1中的第i个元素
y2=[y2,poisscdf(x,lam1(i))];
end
plot(x,y1), figure; %figure命令可让其画两个图
plot(x,y2)注意题目要求是画曲线,所以需要将这些点连起来。
泊松概率密度函数图:
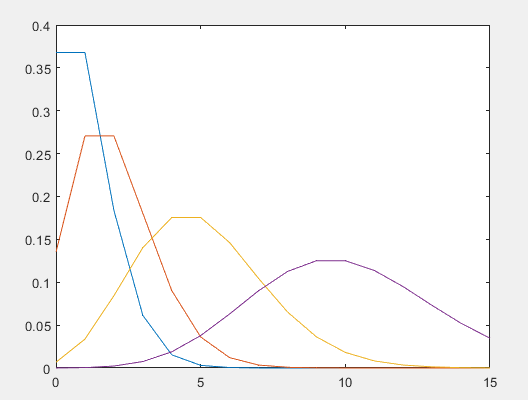
泊松分布的概率分布函数图:
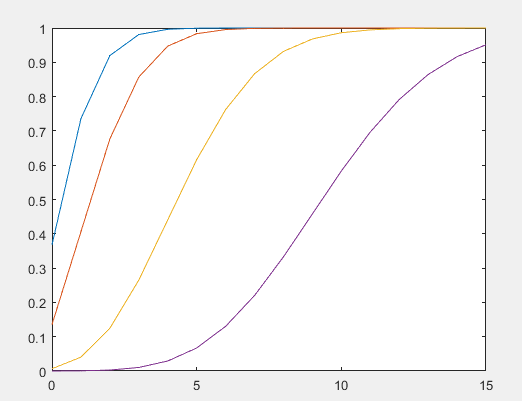
二. 正态分布
2.1 理论部分
正态分布的概率密度函数如下:
其中代表均值,
代表方差。
2.2 MATLAB函数模型
正态分布的概率密度函数,在MATLAB中可以直接调用:
y=normpdf(x,mu,sigma);
%给定x,mu,sigma的值,就可以直接求该点的概率密度值
%注意函数调用格式中的sigma使用的是标准差分布函数(累积概率函数),在MATLAB中可以直接调用:
F=normcdf(x,mu,sigma);如果给定分布函数值,反过来求x,则需要调用逆概率分布函数:
x=norminv(F,mu,sigma);2.3 例题
分别绘制出为(-1,1),(0,0.1),(0,1),(0,10),(1,1)时,正态分布的概率密度函数与分布函数曲线。
MATLAB代码:
x=[-5:.02:5]';
y1=[];
y2=[];
mu1=[-1,0,0,0,1];
sig1=[1,0.1,1,10,1]; sig1=sqrt(sig1); %注意函数调用的是标准差
for i=1:length(mu1) %length(mu1)=5
y1=[y1,normpdf(x,mu1(i),sig1(i))];
y2=[y2,normcdf(x,mu1(i),sig1(i))];
end
plot(x,y1), figure;
plot(x,y2)
正态分布的概率密度函数图:
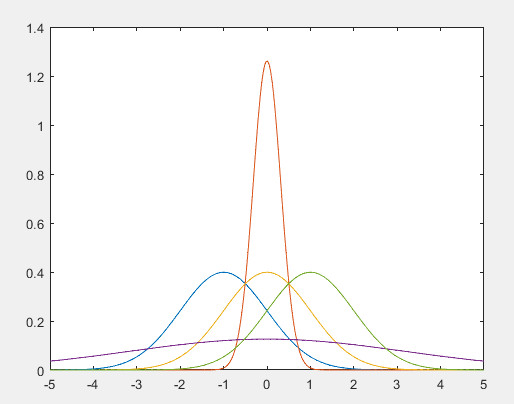
根据对称轴的值,也就是均值的大小可以对应曲线代表的正态分布。方差越大,曲线越胖。
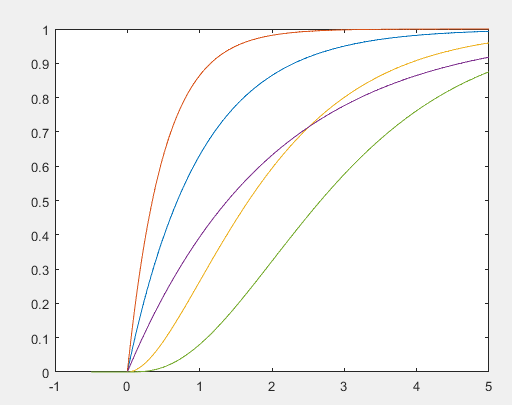
分布函数曲线图:
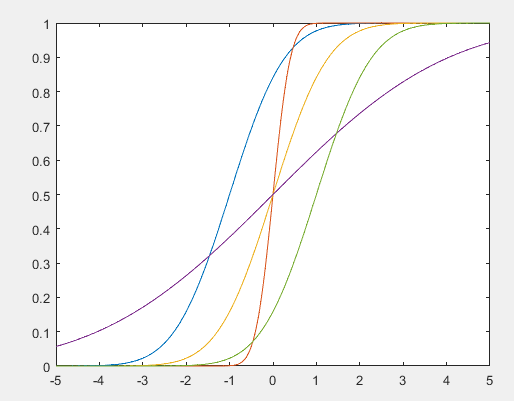
函数严格单调递增。
三. 伽玛分布
3.1 理论部分
观察相邻两个事件之间时间间隔的分布情况,或者隔k个事件的时间间隔的分布情况。根据概率论,事件之间的时间间隔应符合伽玛分布,由于时间间隔可以是任意数值,因此伽玛分布是一种连续概率分布。又因为时间间隔不可能为负数,所以伽玛分布的x需要非负。
伽玛分布有的时候也会写做分布,其概率密度函数为:
伽玛分布需要提前确定两个参数:a与.
上个式子中:
在MATLAB可以调用积分函数来计算该值,也可以直接调用gamma()函数来计算,两种途径都可以。
该积分属于指数积分类型,有三个常用的结论:
3.2 MATLAB函数模型
与泊松分布和正态分布类似,此处也有对应的三个函数,就不过多啰嗦了:
%概率密度函数
y=gampdf(x,a,lambda)
%概率分布函数
F=gamcdf(x,a,lambda)
%逆概率分布函数
x=gaminv(F,a,lambda)3.3 例题
绘制为(1,1),(1,0.5),(2,1),(1,2),(3,1)时伽玛分布的概率密度函数与分布函数曲线。
MATLAB代码:
x=[-0.5:.02:5]'; %图像x轴取值范围
y1=[]; y2=[];
a1=[1,1,2,1,3];
lam1=[1,0.5,1,2,1];
for i=1:length(a1)
y1=[y1,gampdf(x,a1(i),lam1(i))];
y2=[y2,gamcdf(x,a1(i),lam1(i))];
end
plot(x,y1), figure; plot(x,y2)概率密度函数曲线:
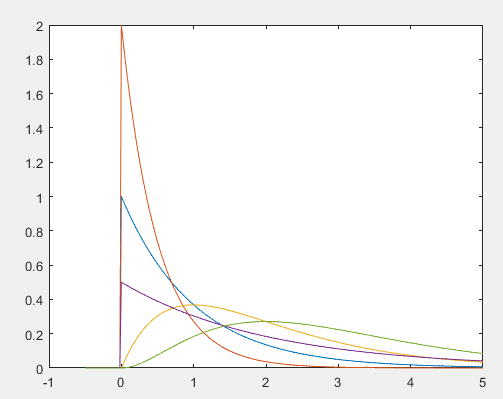
伽马函数的图像趋势一般是先上升后下降。
分布函数曲线: