用编程解决习题【计算机图像处理】

前言
版权
- 第三章 03采样量化与像素间关系
- - 三种距离计算
  - 编程
- 第六章 06图像的直方图变换
- - 均衡化直方图
  - 编程
  - 规定化直方图
  - 编程
- 第七章 07图像的噪声抑制
- - 均值滤波中值滤波计算
  - 编程
  - knn滤波计算
  - 编程
- 第十章 10二值图像的分析
- - 贴标签膨胀腐蚀
  - 编程
最后

前言

2023-12-27 21:11:27

以下内容源自《【计算机图像处理】》
仅供学习交流使用

版权

禁止其他平台发布时删除以下此话
本文首次发布于CSDN平台
作者是CSDN@日星月云
博客主页是https://jsss-1.blog.csdn.net
禁止其他平台发布时删除以上此话

第三章 03采样量化与像素间关系

三种距离计算

一、请计算像素点a(0,1)和像素点b（6,9）之间的欧氏距离，棋盘距离以及城区距离。

欧氏距离：((6-0)^2+(9-1)^2)^0.5=10   345 6810勾股数
棋盘距离：max(|0-6|,|1-9|)=8
城区距离:(|0-6|+|1-9|)=14

编程

import java.util.Scanner;

/**
 * 第三章作业
 *
 * 2023-12-27 21:19:15
 *
 * 一、请计算像素点a(0,1)和像素点b（6,9）之间的欧氏距离，棋盘距离以及城区距离。
 *  欧氏距离：((6-0)^2+(9-1)^2)^0.5=10   345 6810勾股数
 *  棋盘距离：max(|0-6|,|1-9|)=8
 *  城区距离:(|0-6|+|1-9|)=14
 *
 *
 *
 */
public class Main3 {
    static class Point{
        int x;
        int y;

        public Point(){

        }

        public Point(int x,int y){
            this.x=x;
            this.y=y;
        }

        //欧式距离
        public static double distance1(Point p1,Point p2){
            return Math.sqrt(Math.pow(p1.x-p2.x,2)+Math.pow(p1.y-p2.y,2));
        }

        //棋盘距离
        public static double distance2(Point p1,Point p2){
            return Math.max(Math.abs(p1.x-p2.x),Math.abs(p1.y-p2.y));
        }

        //城区距离
        public static double distance3(Point p1,Point p2){
            return Math.abs(p1.x-p2.x)+Math.abs(p1.y-p2.y);
        }


    }


    public static Point p1;
    public static Point p2;

    //手动改值初始化
    public static void init(){
        p1=new Point(0,1);
        p2=new Point(6,9);
    }

    //自动输入初始化
    //0 1 6 9
    static void input() {
        Scanner scanner=new Scanner(System.in);
        int x1=scanner.nextInt();
        int y1=scanner.nextInt();
        int x2=scanner.nextInt();
        int y2=scanner.nextInt();
        p1=new Point(x1,y1);
        p2=new Point(x2,y2);
    }

    public static void main(String[] args) {
//        input(); //输入

        init();//手动改值
        System.out.println(Point.distance1(p1,p2));//10.0
        System.out.println(Point.distance2(p1,p2));//8.0
        System.out.println(Point.distance3(p1,p2));//14.0

    }




}

第六章 06图像的直方图变换

均衡化直方图

一幅灰度级为8的图像对应的归一化直方图为[0.17，0.25，0.21，0.16，0.07，0.08，0.04，0.02]。用列表法计算直方图均衡化后图像的灰度级和对应的概率，并画出处理前后直方图的对比图。

原始灰度级k	0	1	2	3	4	5	6	7
原始直方图sk	0.17	0.25	0.21	0.16	0.07	0.08	0.04	0.02
累计直方图tk	0.17	0.42	0.63	0.79	0.86	0.94	0.98	1.0
扩展取整	1	2	4	5	6	6	6	7
映射	0->1	1->2	2->4	3->5	4->6	5->6	6->6	7->7
均衡化直方图		0.17	0.25		0.21	0.16	0.19	0.02

编程

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class Main6 {

    //原始直方图
    static double[] sk;

    static int n;

    static int l;

    //累计直方图
    static double[] tk;

    //扩展取整
    static int [] extend;

    //均衡化后的直方图
    static double[] equalized;


    //手动改值初始化
    public static void init(){
        sk =new double[]{0.17,0.25,0.21,0.16,0.07,0.08,0.04,0.02};
        n= sk.length;
        l= n-1;
    }

    //自动输入初始化
    //8
    //0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02
    static void input() {
        Scanner scanner=new Scanner(System.in);
        //输入长度
        n= scanner.nextInt();
        l=n-1;
        sk =new double[n];
        int c=0;
        for (int i = 0; i < n; i++) {
            sk[c++]= scanner.nextDouble();
        }
    }

    public static void main(String[] args) {
//        input(); //输入


        init();//手动改值

        equalize();

    }

    //均衡化
    public static void equalize(){

        System.out.println("输出原始直方图：");
        System.out.println(Arrays.toString(sk));

        tk=new double[n];
        tk[0]=sk[0];

        for (int i = 1; i < n; i++) {
            tk[i]=tk[i-1]+sk[i];
        }

        System.out.println("输出累计直方图：");
        System.out.println(Arrays.toString(tk));

        extend=new int[n];
        for (int i = 0; i < n; i++) {
            extend[i]=(int)(tk[i]*l);
        }
        System.out.println("输出扩展取整：");
        System.out.println(Arrays.toString(extend));


        ArrayList<ArrayList<Integer>> map=new ArrayList<>();
        for (int i = 0; i < n; i++) {
            map.add(new ArrayList<>());
        }
        for (int i = 0; i < n; i++) {
            map.get(extend[i]).add(i);
        }

        System.out.println("输出映射关系：");
        for (int i = 0; i < n; i++) {
            ArrayList<Integer> cur=map.get(i);
            if (!cur.isEmpty()){
                System.out.print(cur+"->"+i+"\t");
            }
        }
        System.out.println();


        equalized=new double[n];
        for (int i = 0; i < n; i++) {
            ArrayList<Integer> cur=map.get(i);
            if (!cur.isEmpty()){
                for (Integer j : cur) {
                    equalized[i]+=sk[j];
                }
            }
        }

        System.out.println("输出均衡化的直方图：");
        System.out.println(Arrays.toString(equalized));

    }
}

输出原始直方图：
[0.17, 0.25, 0.21, 0.16, 0.07, 0.08, 0.04, 0.02]
输出累计直方图：
[0.17, 0.42000000000000004, 0.63, 0.79, 0.8600000000000001, 0.9400000000000001, 0.9800000000000001, 1.0]
输出扩展取整：
[1, 2, 4, 5, 6, 6, 6, 7]
输出映射关系：
[0]->1	[1]->2	[2]->4	[3]->5	[4, 5, 6]->6	[7]->7	
输出均衡化的直方图：
[0.0, 0.17, 0.25, 0.0, 0.21, 0.16, 0.19000000000000003, 0.02]

规定化直方图

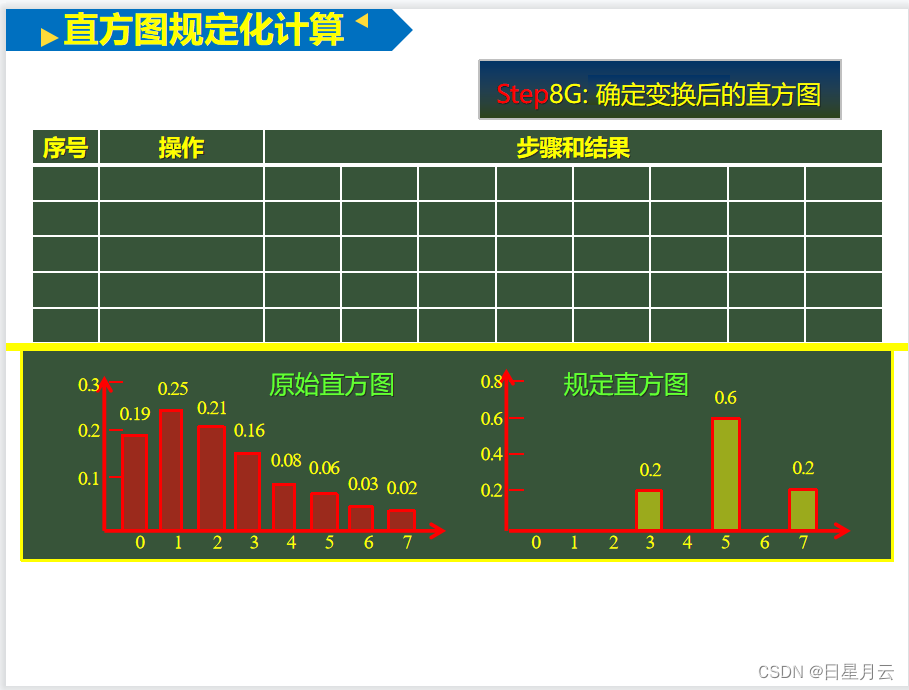
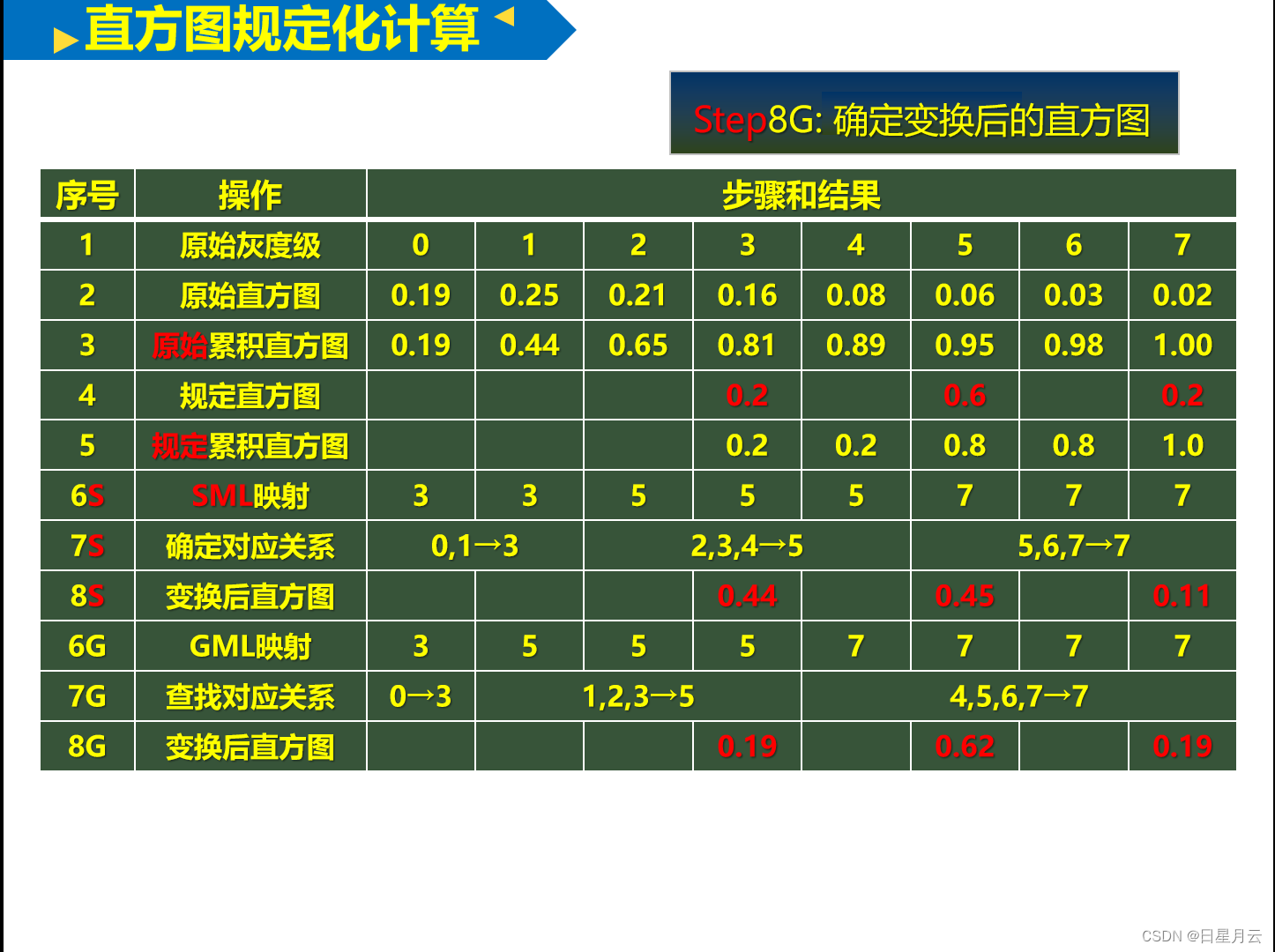
请添加图片描述

编程

import java.util.Arrays;
import java.util.Scanner;

public class Main6_2 {

    //原始直方图
    static double[] sk;

    static int n;

    static int l;

    //累计直方图
    static double[] tk;

    //扩展取整
    static int [] extend;

    //均衡化后的直方图
    static double[] equalized;


    //手动改值初始化
    public static void init1(){
        sk =new double[]{0.19,0.25,0.21,0.16,0.08,0.06,0.03,0.02};
        n= sk.length;
        l= n-1;
    }

    //自动输入初始化
    /*
    8
    0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02
    */
    static void input1() {
        Scanner scanner=new Scanner(System.in);
        //输入长度
        n= scanner.nextInt();
        l=n-1;
        sk =new double[n];
        int c=0;
        for (int i = 0; i < n; i++) {
            sk[c++]= scanner.nextDouble();
        }
    }

    public static void init2(){
        sk =new double[]{0,0,0,0.2,0,0.6,0,0.2};
        n= sk.length;
        l= n-1;
    }

    /*
    8
    0 0 0 0.2 0 0.6 0 0.2
     */
    static void input2() {
        Scanner scanner=new Scanner(System.in);
        //输入长度
        n= scanner.nextInt();
        l=n-1;
        sk =new double[n];
        int c=0;
        for (int i = 0; i < n; i++) {
            sk[c++]= scanner.nextDouble();
        }
    }

    static double[] sk1;



    public static void main(String[] args) {

        double[] tk1 = op1();

        double[] tk2 = op2();

        sml(tk1,tk2);

        gml(tk1,tk2);

    }



    private static double[] op1() {
        //输入原始直方图
//        input1(); //输入
        init1();//手动改值

        sk1=new double[n];
        for (int i = 0; i < n; i++) {
            sk1[i]=sk[i];
        }

        System.out.println("原始直方图");
        System.out.println(Arrays.toString(sk1));

        step1();

        double[] tk1=new double[n];
        for (int i = 0; i < n; i++) {
            tk1[i]=tk[i];
        }
        System.out.println("原始累积直方图");
        System.out.println(Arrays.toString(tk1));

        record1=new int[n];
        for (int i = 0; i < n; i++) {
            record1[i]=record[i];
        }
        System.out.println("record1");
        System.out.println(Arrays.toString(record1));
        return tk1;
    }

    private static double[] op2() {
        //输入规定直方图
//        input1(); //输入
        init2();//手动改值

        System.out.println("规定直方图");
        System.out.println(Arrays.toString(sk));

        step1();

        double[] tk2=new double[n];
        for (int i = 0; i < n; i++) {
            tk2[i]=tk[i];
        }

        System.out.println("规定累积直方图");
        System.out.println(Arrays.toString(tk2));

        record2=new int[n];
        for (int i = 0; i < n; i++) {
            record2[i]=record[i];
        }
        System.out.println("record2");
        System.out.println(Arrays.toString(record2));
        return tk2;
    }

    //就是tk1距离tk2中的哪个最近，则tk1的下标对应tk2中的下标
    //因为都是非递减数列，所以使用双指针就好了，只是O(n)的复杂度

    //有个问题就是可能和原来的不对应，就是原来是0，加了前面的值才有值的
    //所以需要使用record来记录

    public static void sml(double[] tk1,double[] tk2){
        int[] map=new int[n];

        for (int i = 0,j=0 ; i <n; i++) {
            for (; j < n;j++ ) {
                if (j+1==n||Math.abs(tk1[i]-tk2[j])<Math.abs(tk1[i]-tk2[j+1])){
                    break;
                }
            }
            map[i]=record2[j];//不一定是j，而是j所前面的值
        }

        System.out.println("sml映射");
        System.out.println(Arrays.toString(map));

        double[] smled=new double[n];
        for (int i = 0; i < n; i++) {
            smled[map[i]]+=sk1[i];
        }

        System.out.println("变换后直方图");
        System.out.println(Arrays.toString(smled));



    }

    //tk2到tk1的距离
    //因为都是非递减数列，所以使用双指针就好了，只是O(n)的复杂度
    public static void gml(double[] tk1,double[] tk2){
        int[] map=new int[n];

        for (int i = 0,j=0 ; i <n; i++) {
            //跳过为0的或者和之前一样的
            if(tk2[i]==0||(i-1>=0&&tk2[i]==tk2[i-1])){
                continue;
            }
            //只要tk[i]到tk1[j]的距离一直递减就一直映射j->i
            for (; j < n;j++ ) {
                if (j-1<0||Math.abs(tk1[j]-tk2[i])<Math.abs(tk1[j-1]-tk2[i])){
                    map[j]=i;
                }else {
                    break;
                }
            }
        }

        System.out.println("gml映射");
        System.out.println(Arrays.toString(map));

        double[] gmled =new double[n];
        for (int i = 0; i < n; i++) {
            gmled[map[i]]+=sk1[i];
        }

        System.out.println("变换后直方图");
        System.out.println(Arrays.toString(gmled));


    }



    static int[] record;
    static int[] record1;
    static int[] record2;

    private static void step1() {
        record=new int[n];

        tk=new double[n];
        tk[0]=sk[0];

        record[0]=0;

        for (int i = 1; i < n; i++) {
            if(sk[i]==0){
                record[i]=record[i-1];
            }else {
                record[i]=i;
            }
            tk[i]=tk[i-1]+sk[i];
        }

    }



}

原始直方图
[0.19, 0.25, 0.21, 0.16, 0.08, 0.06, 0.03, 0.02]
原始累积直方图
[0.19, 0.44, 0.65, 0.81, 0.89, 0.95, 0.98, 1.0]
record1
[0, 1, 2, 3, 4, 5, 6, 7]
规定直方图
[0.0, 0.0, 0.0, 0.2, 0.0, 0.6, 0.0, 0.2]
规定累积直方图
[0.0, 0.0, 0.0, 0.2, 0.2, 0.8, 0.8, 1.0]
record2
[0, 0, 0, 3, 3, 5, 5, 7]
sml映射
[3, 3, 5, 5, 5, 7, 7, 7]
变换后直方图
[0.0, 0.0, 0.0, 0.44, 0.0, 0.45, 0.0, 0.11]
gml映射
[3, 5, 5, 5, 7, 7, 7, 7]
变换后直方图
[0.0, 0.0, 0.0, 0.19, 0.0, 0.62, 0.0, 0.19]

第七章 07图像的噪声抑制

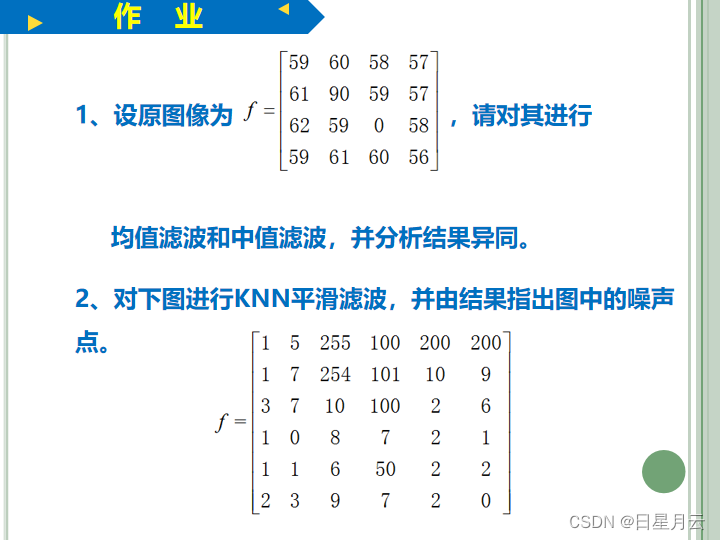
均值滤波中值滤波计算

此处注意，要点明凡是代替的点就是噪声点。
在这里插入图片描述
1.均值滤波
周围所有邻居的平均值
2.中值滤波
周围所有邻居的中位数
3.KNN滤波
周围和他差值最小的K个邻居的平均值

编程


import java.util.Arrays;
import java.util.Scanner;

/**
 *
 * 1、设原图像为
 * 4 4
 * 59 60 58 57
 * 61 90 59 57
 * 62 59 0  58
 * 56 61 60 56
 *
 *
 * 请对其进行均值滤波和中值滤波，并分析结果异同
 *
 *
 */

public class Main7 {

    static int[][] grid;

    static int n;
    static int m;

    //------------------------------------------------------------------------------------

    public static void init(){
        grid= new int[][]{
                {59, 60, 58, 57},
                {61, 90, 59, 57},
                {62, 59, 0, 58},
                {56, 61, 60, 56}
        };
        n= grid.length;
        m=grid[0].length;

    }

    /*
     4 4
     59 60 58 57
     61 90 59 57
     62 59 0  58
     56 61 60 56
     */
    public static void input(){
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        m=scanner.nextInt();
        grid=new int[n][m];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                grid[i][j]=scanner.nextInt();
            }
        }
    }

    //------------------------------------------------------------------------------------


    public static void main(String[] args) {
//        input(); //输入

        init();//手动改值


        System.out.println("输出原始图像");
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(grid[i]));
        }

        System.out.println("输出均值滤波图像");
        int[][] meanFiltered=meanFiltering();
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(meanFiltered[i]));
        }


        //输出中值滤波图像
        System.out.println("输出中值滤波图像");
        int[][] medianFiltered=medianFiltering();
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(medianFiltered[i]));
        }

    }
    
    //------------------------------------------------------------------------------------


    private static int[][] meanFiltering(){
        int[][] meanFiltered=new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                meanFiltered[i][j]=grid[i][j];
            }
        }

        for (int i = 1; i < n-1; i++) {
            for (int j = 1; j < m-1; j++) {
                meanFiltered[i][j]=mean(i,j);
            }
        }


        return meanFiltered;
    }

    //返回(x,y)周围9个点的均值
    // 四舍五入
    private static int mean(int x, int y) {
        int sum=0;
        for (int i = x-1; i <= x+1; i++) {
            for (int j = y-1; j <= y+1; j++) {
                sum+=grid[i][j];
            }
        }
        return (int)(sum/9.0+0.5);
    }

    //------------------------------------------------------------------------------------

    private static int[][] medianFiltering() {
        int[][] medianFiltered=new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                medianFiltered[i][j]=grid[i][j];
            }
        }

        for (int i = 1; i < n-1; i++) {
            for (int j = 1; j < m-1; j++) {
                medianFiltered[i][j]=median(i,j);
            }
        }
        return medianFiltered;
    }

    private static int median(int x, int y) {
        int[] arr=new int[9];
        int c=0;
        for (int i = x-1; i <= x+1; i++) {
            for (int j = y-1; j <= y+1; j++) {
                arr[c++]=grid[i][j];
            }
        }
        Arrays.sort(arr);
        int m=(9+1)/2;
        return arr[m];
    }
    
}

输出原始图像
[59, 60, 58, 57]
[61, 90, 59, 57]
[62, 59, 0, 58]
[56, 61, 60, 56]
输出均值滤波图像
[59, 60, 58, 57]
[61, 56, 55, 57]
[62, 56, 56, 58]
[56, 61, 60, 56]
输出中值滤波图像
[59, 60, 58, 57]
[61, 60, 59, 57]
[62, 61, 59, 58]
[56, 61, 60, 56]

knn滤波计算

编程

/**
 *  2、对下图进行KNN平滑滤波，并由结果指出图中的噪声点。
 *
 *     1 5 255 100 200 200
 *     1 7 254 101 10 9
 *     3 7 10 100 2 6
 *     1 0 8 7 2 1
 *     1 1 6 50 2 2
 *     2 3 9 7 2 0
 */

import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;

public class Main7_2 {
    static int[][] grid;

    static int n;
    static int m;

    static int k=5;

    //------------------------------------------------------------------------------------

    public static void init(){
        grid= new int[][]{
                {1, 5, 255, 100, 200, 200},
                {1, 7, 254, 101, 10, 9},
                {3, 7, 10, 100, 2, 6},
                {1, 0, 8, 7, 2, 1},
                {1, 1, 6, 50, 2, 2},
                {2, 3, 9, 7, 2, 0}
        };
        n= grid.length;
        m=grid[0].length;

    }

    /*
    6 6
    1 5 255 100 200 200
    1 7 254 101 10 9
    3 7 10 100 2 6
    1 0 8 7 2 1
    1 1 6 50 2 2
    2 3 9 7 2 0
     */
    public static void input(){
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        m=scanner.nextInt();
        grid=new int[n][m];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                grid[i][j]=scanner.nextInt();
            }
        }
    }

    public static void main(String[] args) {
//        input(); //输入

        init();//手动改值


        System.out.println("输出原始图像");
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(grid[i]));
        }

        System.out.println("输出knn滤波图像");
        int[][] knnFiltered=knnFiltering();
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(knnFiltered[i]));
        }


        noise(knnFiltered);

    }

    private static void noise(int[][] knnFiltered) {
        System.out.println("输出是否为噪声点");
        int[][] isNoisePoint=new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if(grid[i][j]!= knnFiltered[i][j]){
                    isNoisePoint[i][j]=1;
                }
            }
        }

        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(isNoisePoint[i]));
        }

        System.out.println("噪声点坐标");
        ArrayList<int[]> noisePoints=new ArrayList<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if(isNoisePoint[i][j]==1){
                    noisePoints.add(new int[]{i,j});
                }
            }
        }
        for (int[] noise:noisePoints) {
            System.out.print("("+noise[0]+","+noise[1]+")\t");
        }
        System.out.println();
    }

    private static int[][] knnFiltering() {
        int[][] knnFiltered=new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                knnFiltered[i][j]=grid[i][j];
            }
        }

        for (int i = 1; i < n-1; i++) {
            for (int j = 1; j < m-1; j++) {
                knnFiltered[i][j]=knn(i,j);
            }
        }
        return knnFiltered;

    }

    private static int knn(int x, int y) {

        //优先队列：差值 和 本身的值
        PriorityQueue<int[]> queue=new PriorityQueue<>((a,b)->a[0]-b[0]);
        //按差值排列

        for (int i = x-1; i <= x+1; i++) {
            for (int j = y-1; j <= y+1; j++) {
                queue.add(new int[]{Math.abs(grid[i][j]-grid[x][y]),grid[i][j]});
            }
        }


        int sum=0;
        for (int i = 0; i < k; i++) {
            sum+=queue.poll()[1];
        }
        return (int)(1.0*sum/k+0.5);

    }

}

输出原始图像
[1, 5, 255, 100, 200, 200]
[1, 7, 254, 101, 10, 9]
[3, 7, 10, 100, 2, 6]
[1, 0, 8, 7, 2, 1]
[1, 1, 6, 50, 2, 2]
[2, 3, 9, 7, 2, 0]
输出knn滤波图像
[1, 5, 255, 100, 200, 200]
[1, 6, 162, 64, 25, 9]
[3, 7, 8, 46, 4, 6]
[1, 1, 8, 7, 2, 1]
[1, 1, 7, 16, 2, 2]
[2, 3, 9, 7, 2, 0]
输出是否为噪声点
[0, 0, 0, 0, 0, 0]
[0, 1, 1, 1, 1, 0]
[0, 0, 1, 1, 1, 0]
[0, 1, 0, 0, 0, 0]
[0, 0, 1, 1, 0, 0]
[0, 0, 0, 0, 0, 0]
噪声点坐标
(1,1)	(1,2)	(1,3)	(1,4)	(2,2)	(2,3)	(2,4)	(3,1)	(4,2)	(4,3)

第十章 10二值图像的分析

贴标签膨胀腐蚀

在这里插入图片描述

1）

原始图像
1 1 1 0 0 0
1 0 0 1 0 1
1 0 0 0 0 1
0 0 1 0 1 1
0 1 0 0 1 0
0 0 0 1 0 0

添标签
1 1 1 0 0 0
1 0 0 1 0 2
1 0 0 0 0 2
0 0 3 0 2 2
0 3 0 0 2 0
0 0 0 2 0 0

2）

原始图像
1 1 1 0 0 0
1 0 0 1 0 1
1 0 0 0 0 1
0 0 1 0 1 1
0 1 0 0 1 0
0 0 0 1 0 0


腐蚀
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0


膨胀
1 1 1 1 1 0
1 0 0 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
0 1 1 1 1 0
0 0 0 1 0 0

编程

import java.util.Arrays;
import java.util.Scanner;

/**
 *
 * 设一个二值图像为
     1 1 1 0 0 0
     1 0 0 1 0 1
     1 0 0 0 0 1
     0 0 1 0 1 1
     0 1 0 0 1 0
     0 0 0 1 0 0
 * 1)在8连通意义下，对该图贴标签
 * 2)对上图分别进行一次腐蚀和膨胀运算，结构元素为S=[[1,0],[1,1]]
 * 结构元素原点在S的 (1,1) 坐标处




 */

public class Main8 {

    static int[][] grid;

    static int n;
    static int m;

    static int k=2;
    static int[][] s=new int[][]{
            {1,0},
            {1,1}
    };

    //------------------------------------------------------------------------------------

    public static void init(){
        grid= new int[][]{
                {1, 1, 1, 0, 0, 0},
                {1, 0, 0, 1, 0, 1},
                {1, 0, 0, 0, 0, 1},
                {0, 0, 1, 0, 1, 1},
                {0, 1, 0, 0, 1, 0},
                {0, 0, 0, 1, 0, 0}
        };
        n= grid.length;
        m=grid[0].length;

    }

    /*
     6 6
     1 1 1 0 0 0
     1 0 0 1 0 1
     1 0 0 0 0 1
     0 0 1 0 1 1
     0 1 0 0 1 0
     0 0 0 1 0 0
     */
    public static void input(){
        Scanner scanner=new Scanner(System.in);
        n=scanner.nextInt();
        m=scanner.nextInt();
        grid=new int[n][m];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                grid[i][j]=scanner.nextInt();
            }
        }
    }

    //------------------------------------------------------------------------------------


    public static void main(String[] args) {
//        input(); //输入

        init();//手动改值


        System.out.println("输出原始图像");
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(grid[i]));
        }

        int[][] label=labeling();
        System.out.println("输出标签图像");
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(label[i]));
        }


        int[][] corrosion=corrode();
        System.out.println("输出腐蚀图像");
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(corrosion[i]));
        }

        int[][] expansion=expand();
        System.out.println("输出膨胀图像");
        for (int i = 0; i < n; i++) {
            System.out.println(Arrays.toString(expansion[i]));
        }



    }

    static boolean[][] visited;
    static int labelCount=1;

//    /*
    //8邻域
    static int[][] step=new int[][]{
            {-1,-1},{-1,0},{-1,1},
            {0,-1},{0,1},
            {1,-1},{1,0},{1,1}
    };


    static int stepN=8;
//     */

    /*
    //4邻域
    static int[][] step=new int[][]{
           {-1,0}, {0,-1}, {0,1}, {1,0}
    };

    static int stepN=4;
     */


    private static int[][] labeling() {
        int[][] label=new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                label[i][j]=grid[i][j];
            }
        }

        visited=new boolean[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j]==1){
                    if (!visited[i][j]){
                        dfs(i,j,label);
                        labelCount++;
                    }
                }
            }
        }

        return label;

    }

    private static void dfs(int x, int y,int[][] label) {
        visited[x][y]=true;
        label[x][y]=labelCount;
        for (int i = 0; i < stepN; i++) {
            int nextX=x+step[i][0];
            int nextY=y+step[i][1];
            if(nextX>=0&&nextX<n&&nextY>=0&&nextY<m){
                if (grid[nextX][nextY]==1){
                    if (!visited[nextX][nextY]){
                        dfs(nextX,nextY,label);
                    }
                }
            }
        }
    }


    //------------------------------------------------------------------------------------

    //求腐蚀图像
    private static int[][] corrode(){
        int[][] corrosion=new int[n][m];

        for (int i = 0; i < n-1; i++) {
            for (int j = 0; j < m-1; j++) {
                if (grid[i][j]==1){
                    corrosion[i][j]=co(i,j);
                }
            }
        }

        return corrosion;
    }



    //腐蚀操作
    private static int co(int x, int y) {
        //是否被腐蚀
        int flag=1;
        for (int i = 0; i < k; i++) {
            for (int j = 0; j < k; j++) {
                if(s[i][j]==1){
                    if (grid[x+i][y+j]!=1){
                        flag=0;
                        break;
                    }
                }
            }
            if (flag==0){
                break;
            }
        }
        return flag;
    }

    //------------------------------------------------------------------------------------

    //求膨胀图像
    private static int[][] expand() {
        int[][] expansion=new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                expansion[i][j]=grid[i][j];
            }
        }

        for (int i = 0; i < n-1; i++) {
            for (int j = 0; j < m-1; j++) {
                if (grid[i][j]==0){
                    expansion[i][j]=ex(i,j);
                }
            }
        }
        return expansion;
    }

    //膨胀操作
    private static int ex(int x, int y) {
        //是否被膨胀
        int flag=0;
        for (int i = 0; i < k; i++) {
            for (int j = 0; j < k; j++) {
                if(s[i][j]==1){
                    if (grid[x+i][y+j]==1){
                        flag=1;
                        break;
                    }
                }
            }
            if (flag==1){
                break;
            }
        }
        return flag;
    }

}

输出原始图像
[1, 1, 1, 0, 0, 0]
[1, 0, 0, 1, 0, 1]
[1, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 1, 1]
[0, 1, 0, 0, 1, 0]
[0, 0, 0, 1, 0, 0]
输出标签图像
[1, 1, 1, 0, 0, 0]
[1, 0, 0, 1, 0, 2]
[1, 0, 0, 0, 0, 2]
[0, 0, 3, 0, 2, 2]
[0, 3, 0, 0, 2, 0]
[0, 0, 0, 2, 0, 0]
输出腐蚀图像
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0]
输出膨胀图像
[1, 1, 1, 1, 1, 0]
[1, 0, 0, 1, 1, 1]
[1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1]
[0, 1, 1, 1, 1, 0]
[0, 0, 0, 1, 0, 0]

4邻域下的贴标签

输出原始图像
[1, 1, 1, 0, 0, 0]
[1, 0, 0, 1, 0, 1]
[1, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 1, 1]
[0, 1, 0, 0, 1, 0]
[0, 0, 0, 1, 0, 0]
输出标签图像
[1, 1, 1, 0, 0, 0]
[1, 0, 0, 2, 0, 3]
[1, 0, 0, 0, 0, 3]
[0, 0, 4, 0, 3, 3]
[0, 5, 0, 0, 3, 0]
[0, 0, 0, 6, 0, 0]