相机种类:
当拿到一款需要标定内参的相机时,第一个问题就是选择那种的相机模型。工程上相机类型的划分并不是十分严格,一般来说根据相机FOV可以把相机大概分为以下几类:
长焦相机:<=
标准相机:~
;
广角相机:~
;
鱼眼相机:>。
这里按角度的划分并不是绝对严格,临界处的相机用两种模型中的任意一种都可以。
有时也可能会遇到变焦相机和定焦相机之分,但变焦相机在标定内参时也需要固定焦距,因此也可以划分到上面几类。这里需要注意内参和焦距的严格对应的,当调焦后需要重新标定相机内参。
不同角度的相机需要选择不同的相机模型来标定相机内参。相机模型又分为投影模型和畸变模型。接下来分别进行讨论。
长焦相机:
长焦相机的标定一般采用针孔相机模型,但在实际标定中我们很难通过标定板来标定长焦相机。长焦相机的景深太大,普通标定板由于尺寸较小会导致其在采集的图像中所占区域太小,无法提供足够的约束来标定外参。如果强行在近处采集标定板图像,会造成图像上标定图像模糊不清,从而导致角点提取误差较大,甚至失败。因此标定时计算外参会有非常大的误差,又因为相机内参和外参在投影时具有耦合的效应,即使重投影误差非常小也无法保证内参的正确性。这也是为什么重投影误差只能作为内参精度的参考,而无法作为衡量标准。
所以一般来说不建议个人去标定长焦相机,即使标定出来结果也很有可能是错误的。之前笔者还是小白的时候尝试使用标定板标定长焦相机,虽然重投影误差很小但内参精度较差,点云投影效果还没有使用相机厂商提供的参考内参值精确。如果必须自己标定的话也不建议用标定板的方式,需要设计新的方法,核心是保证参照物能够提供足够的约束。
标准相机:
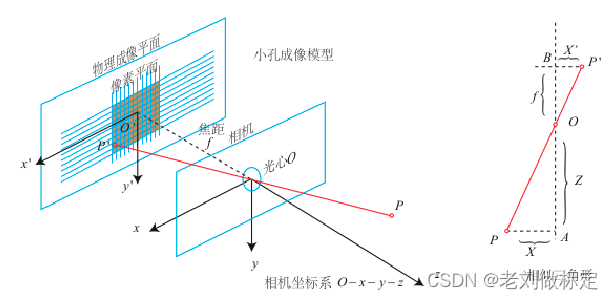
针对标准相机工程上采用针孔相机模型标定。其原理类似于小孔成像,不同之处在于为了增加透光量采用凸透镜。其投影模型为针孔投影模型,原理如下图所示:
接下来考虑其畸变模型,这里需要了解一下概念:径向畸变和切向畸变。
一般来说,制造透镜很难保证曲率和设计的一致,曲率制造的误差会造成相机成像是在径向产生误差即径向畸变。径向畸变主要有以下两种:桶型畸变和枕型畸变。

径向畸变主要描述畸变量和像素到图像中心距离的关系,后续会在具体公式讨论。
同样安装时镜头和成像平面无法保证绝对平行,因此会产生切向畸变:

切向畸变主要描述成像平面和光轴之间的倾斜角度。因此针孔相机模型的畸变模型是径向切向畸变模型。
接下来看如何将相机坐标系下的点投影到图像上:相机坐标系->图像坐标系->像素坐标系。
具体公式如下:
一般投影时先对空间三维点归一化:
其中u v是无畸变点,r描述相机坐标xy轴是否垂直,一般情况下为0。接下来对点加径向畸变:
其中k1 k2 k3是径向畸变参数。有时会遇到k4 k5,也是径向畸变参数,不过一般用到k3就行了。因为径向畸变是泰勒展开的多项式拟合,用到太多畸变参数就会存在过拟合问题反而效果不好。
上面提到的枕型畸变和桶型畸变与k的取值有关,当k都大于零时就会产生枕型畸变,反之则会产生桶型畸变。
接下来再加上切向畸变:
以上就是相机坐标系下点投影到图像上像素的整个过程。
广角相机:
广角相机和鱼眼相机其实都属于鱼眼相机的范畴,只是标定时选择的相机模型不一样。在介绍接下来几种相机模型前还是简单介绍鱼眼相机相关的基础知识以方便理解。

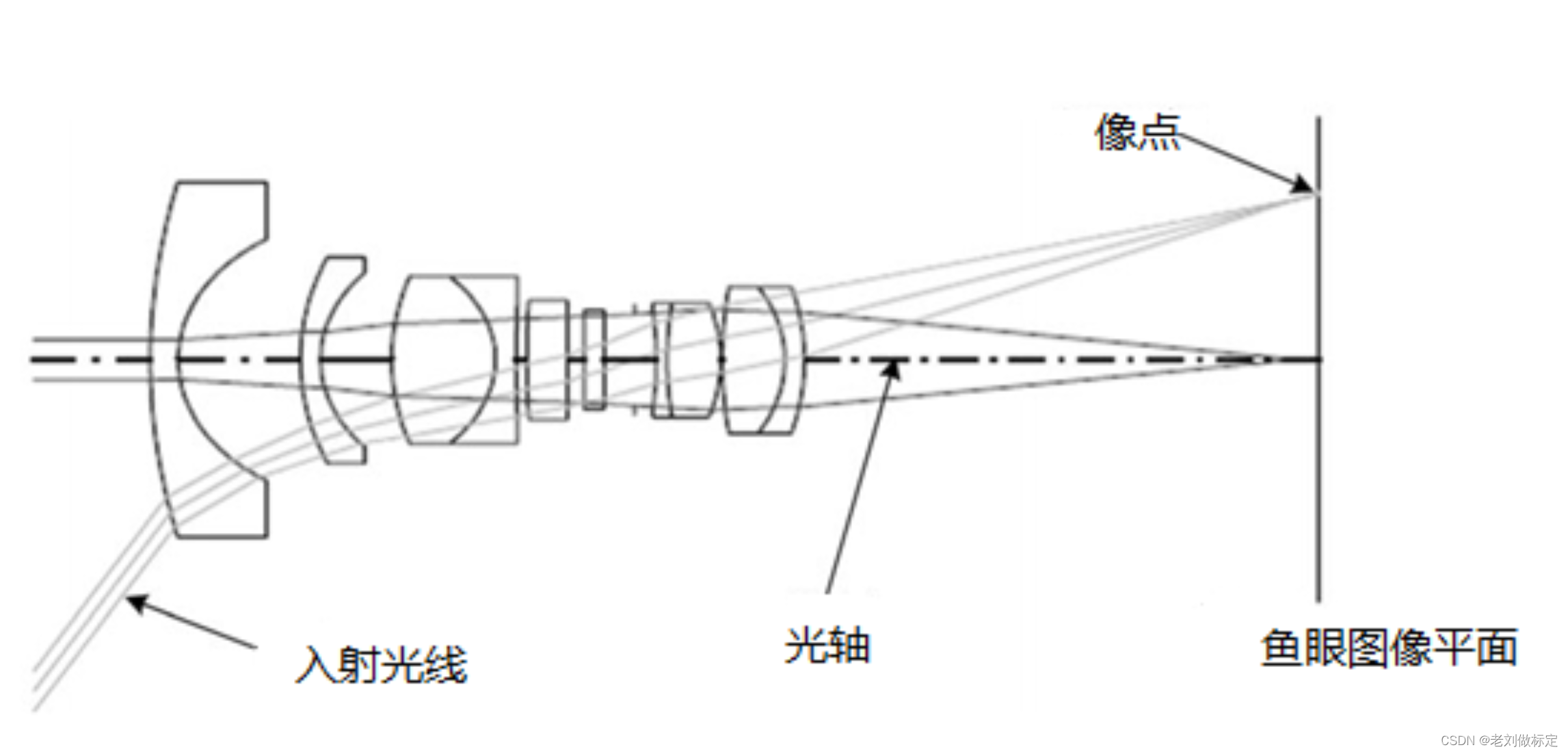
你以为的鱼眼相机 实际的鱼眼相机
我们知道鱼眼相机的初衷是为了让相机看到尽可能大的视野,也就是尽可能将场景中的物体投影到图像上,因此鱼眼相机通过组合多个镜头将光线多次折射到图像平面上。鱼眼相机需要根据某种投影模型进行设计,常见的设计模型主要分为四种:等距投影模型、等立体角投影模型、正交投影模型和体视投影模型。其投影过程如下图所示,除了f*tan()对应针孔投影模型外,其它四种对应上面四种。
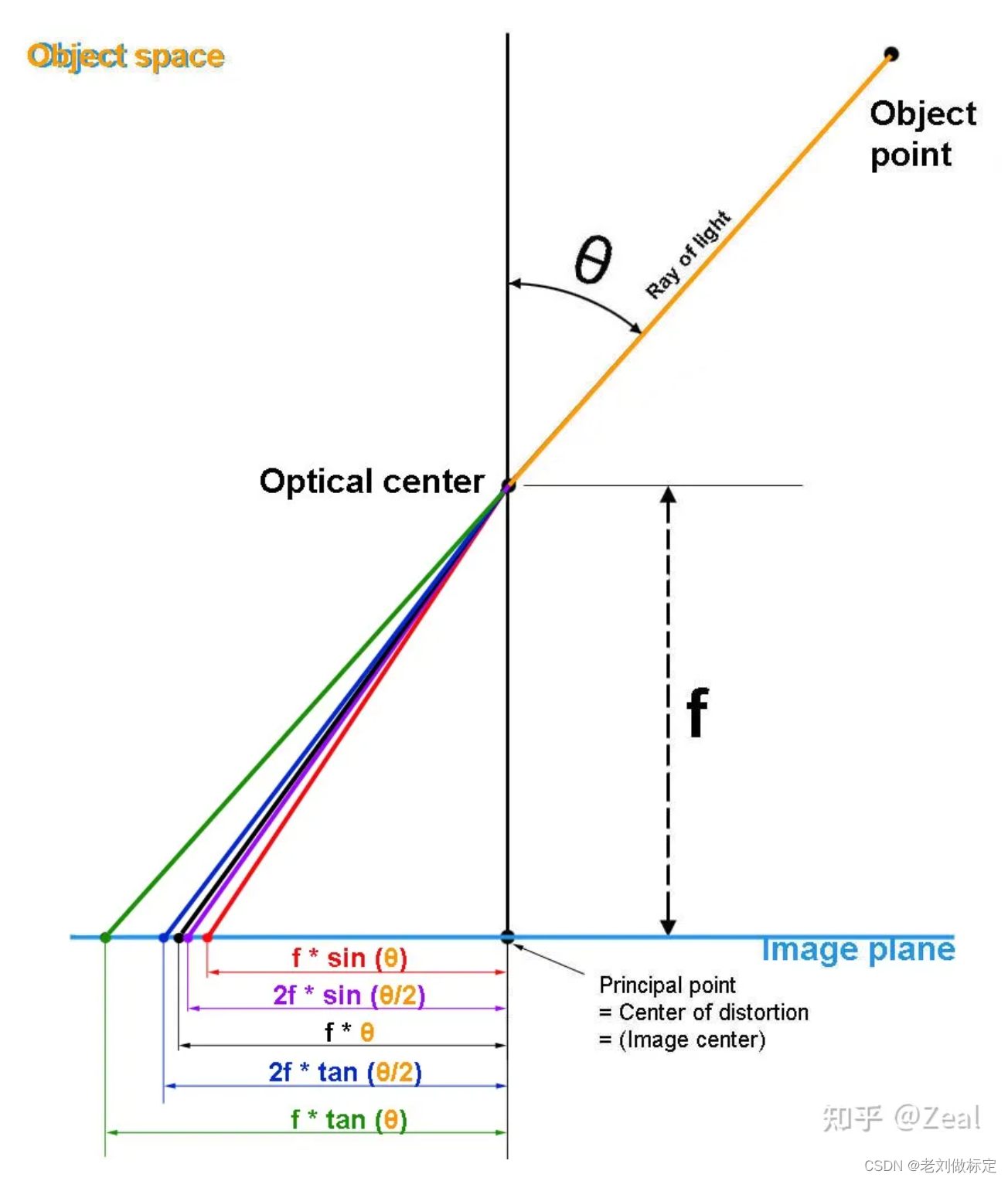
鱼眼相机四种投影模型其中最常用的是等距相机模型,所以主要对等距相机模型进行讨论,其它模型感兴趣自己上网搜索。等距相机模型:

投影公式为:r = f * ,r为成像的高,
为入射角。该模型描述成像的像高和入射角成正比。
广角相机最好选择等距相机模型,OpenCV中使用的模型是由Kannala提出的一种鱼眼相机的一般近似模型。是在等距投影模型的基础上提出来的。接下来对OpenCV中相机模型进行分析。整体过程如下图所示:

这里主要是利用相机模型将世界坐标系下点投影到图像上的过程。第一步是将世界坐标系的点通过外参转到相机坐标系下,然后转到归一化平面上。这时考虑畸变对投影的影响,也可以看出等距相机模型的畸变只考虑了径向畸变没有考虑切向畸变。
已知等距相机模型r = f * ,在实际中很难按设计模型制造,因此使用多项式拟合。最后得到包含畸变后新的
d。接着计算归一化平面上带畸变的投影点
。然后利用针孔投影模型将点投影到图像上。上面公式中有一个
,这个是表征图像平面xy是否垂直的参数,很多情况下默认为0。
鱼眼相机:
作者个人经验,小于180度的相机可以使用OpenCV中相机模型来标定相机,但是如果相机度数大于180度时OpenCV标定出来的效果并不是十分好。
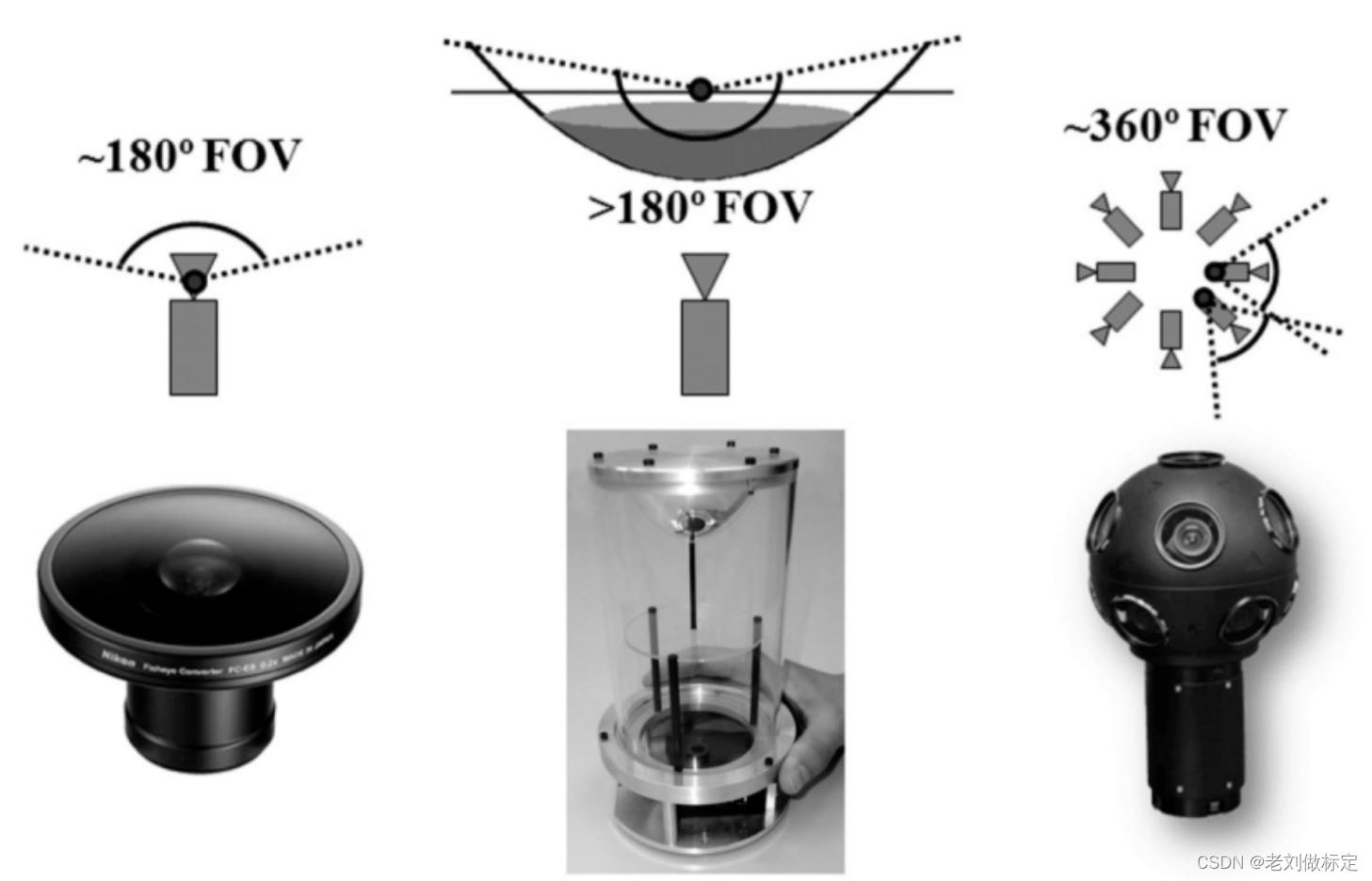
这时标定相机可以用的相机模型有kalibr的MEI模型或是Davide Scaramuzza的ocam相机模型。但在实际应用中ocam相机模型更好一些。

![[SWPUCTF 2021 新生赛]finalrce](https://img-blog.csdnimg.cn/direct/fe8734cca79c42978eda2e5d8ea61ded.png#pic_center)