11、基于LunarLander登陆器的A2C强化学习（含PYTHON工程）

LunarLander复现：
07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）

08、基于LunarLander登陆器的DDQN强化学习（含PYTHON工程）

09、基于LunarLander登陆器的Dueling DQN强化学习（含PYTHON工程）

10、基于LunarLander登陆器的Dueling DDQN强化学习（含PYTHON工程）

11、基于LunarLander登陆器的A2C强化学习（含PYTHON工程）

基于TENSORFLOW2.10

0、实践背景

gym的LunarLander是一个用于强化学习的经典环境。在这个环境中，智能体（agent）需要控制一个航天器在月球表面上着陆。航天器的动作包括向上推进、不进行任何操作、向左推进或向右推进。环境的状态包括航天器的位置、速度、方向、是否接触到地面或月球上空等。

智能体的任务是在一定的时间内通过选择正确的动作使航天器安全着陆，并且尽可能地消耗较少的燃料。如果航天器着陆时速度过快或者与地面碰撞，任务就会失败。智能体需要通过不断地尝试和学习来选择最优的动作序列，以完成这个任务。

下面是训练的结果：
在这里插入图片描述

1、Actor-Critic框架的基本概念

Actor：表演者，一般称为pi(policy)网络，根据该网络的输出参数指导物体的具体动作

Critic：批评者，对Agent的动作或者状态进行打分，使得框架能够量化动作的优劣

Reward：奖励R，指的是客观获得的，例如说消灭了敌人或者吃到了金币等等

Return：回报U，可以理解为获得高奖励的可能，越大代表越可能获得高奖励。实际使用的是折扣回报，因为对于很远的奖励我们还需要考虑时间成本。对于一个随机的环境，在t时刻我们无法获得Ut的具体取值，因为我们不知道未来的奖励。
$U_t=R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+\gamma^3\cdot R_{t+3}+\cdots$

Q(s,a)：动作价值函数，其输入为当前状态和要执行的动作，输出为该动作能带来多大的价值，因此，一种贪心的方法是选择能够使Q(s,a)最大动作执行。
Q(s,a)的维度等于动作空间的维度。打个简单的比方，假设我现在有两个动作，向北去捡芝麻，向南去捡西瓜。从最终获得的奖励来看，西瓜是大于芝麻的，但是如果芝麻就在我桌上，但是西瓜在20km以外，那可能我还是选择芝麻得了。那么动作价值函数可能就是（1，0.1）。1是捡芝麻的动作价值，0.1是捡西瓜的动作价值，虽说西瓜好吃，但是太远了，所以其动作价值打分特别低。

Q(s,a)和Ut关系：Q(s,a)是Ut的期望，期望可以理解为求积分，实际上Q是对Ut把所有t之后的时刻（t+1、t+2等等）当作变量求积分得到的。因此Q(s,a)可以直观反应当前状态s下执行各个动作的好坏。
$Q_\pi(s_t,{a_t})=\mathbb{E}[U_t\mid s_t,{a_t}]$

V(s)：状态价值函数，是Q函数的期望。因为期望的积分动作消去了动作A，因此状态价值函数V可以用来直观的反应一个状态的好坏。其实际上是Q(s,a)对不同a的加权平均。
例如，自家高低三路被破，依据这个状态我们就知道现在的状态打分不太行。状态打分不行的原因是每个动作都不会带来太高的打分（都要输了）。
$V_{\pi}(s_{t})=\mathbb{E}_{{A_{t}}}[Q_{\pi}(s_{t},{A_{t}})\mid s_{t}]$

2、Advantage Actor-Critic理论

A2C(Advantage Actor-Critic)在原来的AC框架上进行改进，主要的改进是其Critic网络不再依赖于动作a，更少的变量减少了其拟合的难度。同时在训练时使用了优势函数，降低了Variance，提升了性能。

具体的推导过程参考【王树森】深度强化学习(DRL)的P16。可能有小伙伴非常好奇，为什么A2C的td error和AC算法的不一致，这些都在上面的视频里面给出了计算过程。

训练的流程图如下所示（小写代表的是实际观测到的值）：
在这里插入图片描述
为什么pi输出网络往往使用终端为softmax的网络进行拟合？
实际上，pi输出网络往往使用终端为softmax的网络进行拟合，因此其pi网络输出的是概率分布。为什么采用这种方法呢，因为log的形式和交叉熵高度接近，如下就是策略网络的梯度公式：
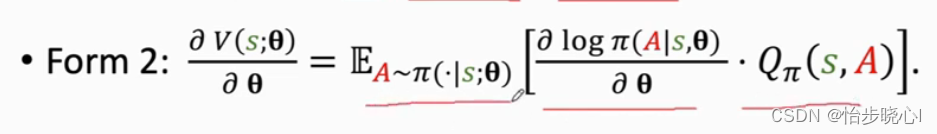
在这里插入图片描述
这是交叉熵的公式，其中策略网络pi实际上就是概率分布（是不是比较一致嘞），当然Q(s,a)会作为sample_weight体现在其中。-参考softmax loss详解，softmax与交叉熵的关系：

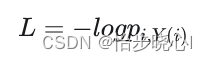
此外，实际训练时会使用baseline而不会直接使用Q(s,a)，也就是下面这个式子
在这里插入图片描述
其中求导乘以后面的那个就是TD error的倒数。

3、Advantage Actor-Critic网络更新流程

在这里插入图片描述

3、Advantage Actor-Critic关键编程实现

3.1、TD Target的计算

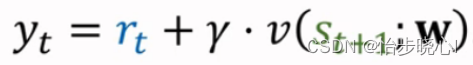
在这里插入图片描述
计算代码如下所示，其中v_value 是使用critic网络预测的下一状态的v，其输入为下一时刻的状态next_state。

    def td_target(self, reward, next_state, done):
        if done:
            return reward
        v_value = self.critic.model(
            np.reshape(next_state, [1, self.state_dim]))
        return np.reshape(reward + self.discount_factor * v_value[0], [1, 1])

3.2、advatnage的计算

advatnage的计算原来是Q-V的形式，但是在A2C算法中Q被近似成了r+gamma*V，也就是所说的TD target：
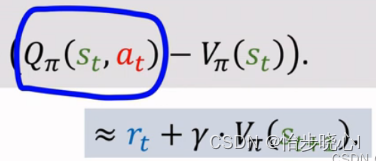
在这里插入图片描述
advatnage计算代码如下：

    def advatnage(self, td_targets, baselines):
        return td_targets - baselines

baselines基于当前时刻的价值网络self.critic.model(state)：

advantage = self.advatnage(
    td_target, self.critic.model(state))

3.3、policy网络的loss计算与梯度下降

policy网络的loss实际上就是在原来的softmax的基础上乘以td error，也就是将td error（advatnage）作为权重。
在这里插入图片描述

    def compute_loss(self, actions, logits, advantages):
        # 输入的logits并不一定是概率分布，因此使用from_logits=True进行额外的归一化
        ce_loss = tf.keras.losses.SparseCategoricalCrossentropy(
            from_logits=True)
        actions = tf.cast(actions, tf.int32)
        policy_loss = ce_loss(
            actions, logits, sample_weight=tf.stop_gradient(advantages))
        return policy_loss

训练代码：

    def train(self, states, actions, advantages):
        with tf.GradientTape() as tape:
            logits = self.model(states, training=True)
            loss = self.compute_loss(
                actions, logits, advantages)
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.opt.apply_gradients(zip(grads, self.model.trainable_variables))
        return loss

3.4、Critic网络的loss计算与梯度下降

上面流程也非常明白，Critic的目的就是让td error为0，所以需要对td error使用均方误差的梯度下降：
在这里插入图片描述

    def compute_loss(self, v_pred, td_targets):
        mse = tf.keras.losses.MeanSquaredError()
        return mse(td_targets, v_pred)

    def train(self, states, td_targets):
        with tf.GradientTape() as tape:
            v_pred = self.model(states, training=True)
            assert v_pred.shape == td_targets.shape
            loss = self.compute_loss(v_pred, tf.stop_gradient(td_targets))
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.opt.apply_gradients(zip(grads, self.model.trainable_variables))
        return loss

4、运行效果展示

agent = Agent('A2C', 4, 8, actor_lr=0.0003, critic_lr=0.0005,
              discount_factor=0.995, batch_size=1)

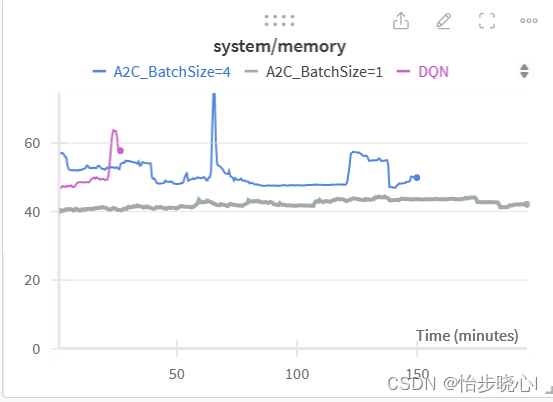
看起来收敛比较快，但是最终结果是不如DQN的，当然我没有仔细去调参。A2C比较为人诟病的就是容易过山车，原来训练不错，突然就跌下去了：
在这里插入图片描述

由于无法使用经验回放训练，其训练速度非常慢：
在这里插入图片描述

5、完整代码(工程在最上方链接)

import base64
from collections import deque

import imageio
import pandas as pd
from matplotlib import pyplot as plt

import wandb
import tensorflow as tf
from keras.layers import Input, Dense
from keras.backend import clear_session
from memory_profiler import profile
import gym
import argparse
import numpy as np


# tf.keras.backend.set_floatx('float64')


class Actor:
    def __init__(self, state_dim, action_dim, actor_lr):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.model = self.create_model()
        self.opt = tf.keras.optimizers.Adam(actor_lr)

    def create_model(self):
        return tf.keras.Sequential([
            Input((self.state_dim,)),
            Dense(256, activation='relu'),
            Dense(256, activation='relu'),
            Dense(self.action_dim, activation='softmax')
        ])

    def compute_loss(self, actions, logits, advantages):
        # 输入的logits并不一定是概率分布，因此使用from_logits=True进行额外的归一化
        ce_loss = tf.keras.losses.SparseCategoricalCrossentropy(
            from_logits=True)
        actions = tf.cast(actions, tf.int32)
        policy_loss = ce_loss(
            actions, logits, sample_weight=tf.stop_gradient(advantages))
        return policy_loss

    def train(self, states, actions, advantages):
        with tf.GradientTape() as tape:
            logits = self.model(states, training=True)
            loss = self.compute_loss(
                actions, logits, advantages)
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.opt.apply_gradients(zip(grads, self.model.trainable_variables))
        return loss


class Critic:
    def __init__(self, state_dim, critic_lr):
        self.state_dim = state_dim
        self.model = self.create_model()
        self.opt = tf.keras.optimizers.Adam(critic_lr)

    def create_model(self):
        return tf.keras.Sequential([
            Input((self.state_dim,)),
            Dense(256, activation='relu'),
            Dense(256, activation='relu'),
            Dense(1, activation='linear')
        ])

    def compute_loss(self, v_pred, td_targets):
        mse = tf.keras.losses.MeanSquaredError()
        return mse(td_targets, v_pred)

    def train(self, states, td_targets):
        with tf.GradientTape() as tape:
            v_pred = self.model(states, training=True)
            assert v_pred.shape == td_targets.shape
            loss = self.compute_loss(v_pred, tf.stop_gradient(td_targets))
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.opt.apply_gradients(zip(grads, self.model.trainable_variables))
        return loss


class Agent:
    def __init__(self, model, num_actions, input_dims, actor_lr=0.0005, critic_lr=0.001,
                 discount_factor=0.995, batch_size=4):

        self.action_dim = num_actions
        self.state_dim = input_dims
        self.actor = Actor(self.state_dim, self.action_dim, actor_lr)
        self.critic = Critic(self.state_dim, critic_lr)
        self.model = model
        self.discount_factor = discount_factor
        self.batch_size = batch_size
        self.target_ave_scores = 500
        self.max_num_timesteps = 1000
        self.num_p_av = 100

    def td_target(self, reward, next_state, done):
        if done:
            return reward
        v_value = self.critic.model(
            np.reshape(next_state, [1, self.state_dim]))
        return np.reshape(reward + self.discount_factor * v_value[0], [1, 1])

    def advatnage(self, td_targets, baselines):
        return td_targets - baselines

    def list_to_batch(self, list):
        batch = list[0]
        for elem in list[1:]:
            batch = np.append(batch, elem, axis=0)
        return batch

    # @profile
    def train(self, env, max_episodes=1000, graph=True):
        wandb.init(name='A2C', project="deep-rl-tf2")
        episodes_history, total_point_history, avg_point_history, target_history = [], [], [], []
        for ep in range(max_episodes):
            state_batch = []
            action_batch = []
            td_target_batch = []
            advatnage_batch = []
            episode_reward, done = 0, False

            state, _ = env.reset()
            for t in range(self.max_num_timesteps):
                # self.env.render()
                state = np.reshape(state, [1, self.state_dim])
                probs = self.actor.model(state)
                probs = np.array(probs)
                probs /= probs.sum()

                action = np.random.choice(self.action_dim, p=probs[0])

                next_state, reward, done, _, _ = env.step(action)

                action = np.reshape(action, [1, 1])
                next_state = np.reshape(next_state, [1, self.state_dim])
                reward = np.reshape(reward, [1, 1])

                td_target = self.td_target(reward * 0.01, next_state, done)
                advantage = self.advatnage(
                    td_target, self.critic.model(state))

                # actor_loss = self.actor.train(state, action, advantage)
                # critic_loss = self.critic.train(state, td_target)

                state_batch.append(state)
                action_batch.append(action)
                td_target_batch.append(td_target)
                advatnage_batch.append(advantage)

                if len(state_batch) >= self.batch_size or done:
                    states = self.list_to_batch(state_batch)
                    actions = self.list_to_batch(action_batch)
                    td_targets = self.list_to_batch(td_target_batch)
                    advantages = self.list_to_batch(advatnage_batch)

                    actor_loss = self.actor.train(states, actions, advantages)
                    critic_loss = self.critic.train(states, td_targets)

                    state_batch = []
                    action_batch = []
                    td_target_batch = []
                    advatnage_batch = []

                episode_reward += reward[0][0]
                state = next_state[0]
                if done:
                    break

            episodes_history.append(ep)
            target_history.append(self.target_ave_scores)
            total_point_history.append(episode_reward)
            av_latest_points = np.mean(total_point_history[-self.num_p_av:])
            avg_point_history.append(av_latest_points)

            wandb.log({'target_ave_scores': 300, 'epoch': ep})
            wandb.log({'total_points': episode_reward, 'epoch': ep})
            wandb.log({'av_latest_points': av_latest_points, 'epoch': ep})

            print(
                f"\rEpisode {ep + 1} | Total point average of the last {self.num_p_av} episodes: {av_latest_points:.2f}",
                end="")

            if (ep + 1) % self.num_p_av == 0:
                print(
                    f"\rEpisode {ep + 1} | Total point average of the last {self.num_p_av} episodes: {av_latest_points:.2f}")

            # We will consider that the environment is solved if we get an
            # average of 200 points in the last 100 episodes.
            if av_latest_points >= self.target_ave_scores or ep + 1 == max_episodes:
                print(f"\n\nEnvironment solved in {ep + 1} episodes!")
                self.actor.model.save('saved_networks/' + self.model + '/lunar_lander_model_actor.h5')
                self.critic.model.save('saved_networks/' + self.model + '/lunar_lander_model_critic.h5')
                break

            if graph:
                df = pd.DataFrame({'x': episodes_history, 'Score': total_point_history,
                                   'Average Score': avg_point_history, 'Solved Requirement': target_history})

                plt.plot('x', 'Score', data=df, marker='', color='blue', linewidth=2, label='Score')
                plt.plot('x', 'Average Score', data=df, marker='', color='orange', linewidth=2, linestyle='dashed',
                         label='AverageScore')
                plt.plot('x', 'Solved Requirement', data=df, marker='', color='red', linewidth=2, linestyle='dashed',
                         label='Solved Requirement')
                plt.legend()
                plt.savefig('LunarLander_Train_' + self.model + '.png')

    def test_create_video(self, env, filename, model_name, fps=30):
        self.actor.model = tf.keras.models.load_model(model_name)
        with imageio.get_writer(filename, fps=fps) as video:
            done = False
            state, _ = env.reset()
            frame = env.render()
            video.append_data(frame)
            episode_score = 0
            for t in range(self.max_num_timesteps):
                state = np.reshape(state, [1, self.state_dim])
                probs = self.actor.model(state)
                action = np.argmax(probs.numpy()[0])
                state, reward, done, _, _ = env.step(action)
                episode_score += reward
                frame = env.render()
                video.append_data(frame)
                if done:
                    break
            print(f'episode_score:', episode_score)
            """Embeds an mp4 file in the notebook."""
            video = open(filename, 'rb').read()
            b64 = base64.b64encode(video)
            tag = '''
            <video width="840" height="480" controls>
            <source src="data:video/mp4;base64,{0}" type="video/mp4">
            Your browser does not support the video tag.
            </video>'''.format(b64.decode())
            # return IPython.display.HTML(tag)


def main():
    myModel = 'A2C'
    env = gym.make('LunarLander-v2', render_mode='rgb_array')
    agent = Agent('A2C', 4, 8, actor_lr=0.0003, critic_lr=0.0005,
                  discount_factor=0.995, batch_size=4)
    # 取消注释以进行训练
    agent.train(env)
    # agent.test_create_video(env, filename='Lunar_Lander_videos/lunar_lander' + myModel + '.mp4',
    #                         model_name='saved_networks/' + myModel + '/lunar_lander_model_actor.h5', fps=30)


if __name__ == "__main__":
    main()