1 任务介绍

事件关系抽取：文本中包含多个事件e₁,e₂,…,e_n，识别每个事件对(e_i,e_j)之间的关系r(e_i,e_j)

• 子事件(Subevent)关系抽取：{PARENT-CHILD, CHILD-PARENT, COREF, NOREL}
• 事件时序(Temporal)关系抽取：{BEFORE, AFTER, EQUAL, VAGUE}

主流的方法都是采用Vector-based的方法，将文本和所有类别标签表征成向量，然后采用Multi-class Classification的方法逐个判断是否属于某个关系类型。此类方法存在难以保证逻辑约束连贯性的缺陷，例如对称性：

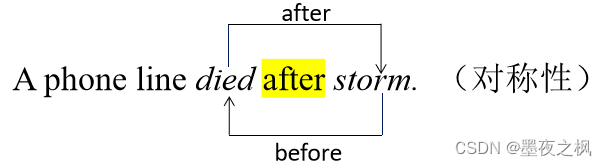
提出Box Event Relation Extraction(BERE)模型，旨在修改底层的模型，使用Box Embedding的表征方法，通过将每个事件表示为一个Box Representation，把任务对象都用超矩形(Hyperrectangle)来表征，这样可以用矩形是否包含或重叠来识别其归属。

逻辑约束：主要针对关系的反对称约束(Asymmetry)和连接约束(Conjunctive)

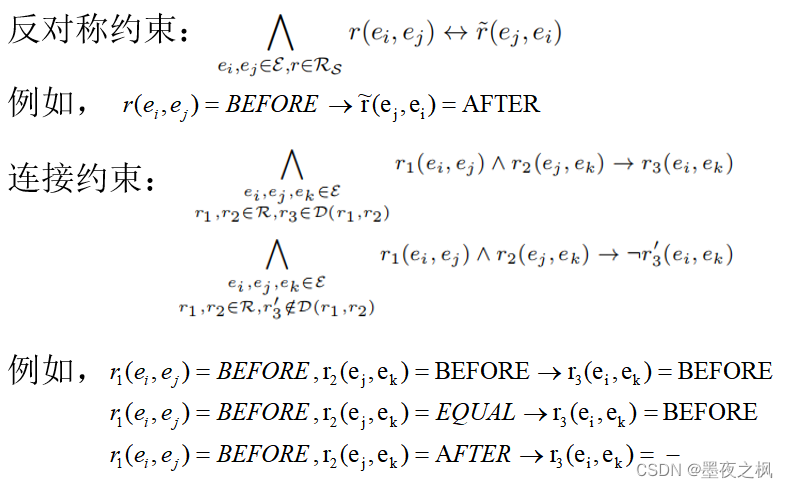
连接约束：关于时序关系和子事件关系的连接约束的归纳法表
给定三个事件e_i,e_j和e_k，最左边一列表示r₁(e_i,e_j)，最上面一行表示r₂(e_j,e_k)

2 Box Embedding

首先引入超矩形将层次图节点嵌入到欧几里得空间，随后扩展到联合嵌入多关系图并执行逻辑查询。

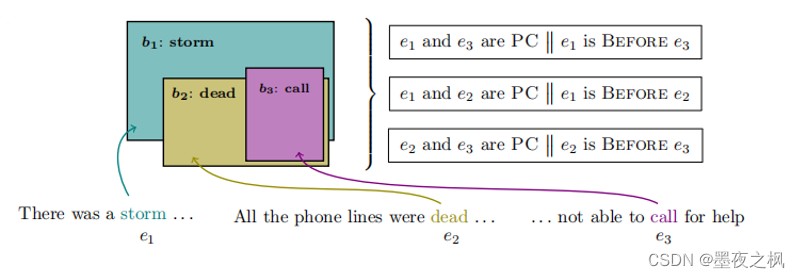
Box Embedding不仅保留了它们的语义信息，而且可以根据逻辑约束推断出事件e₁是在事件e₃之前。

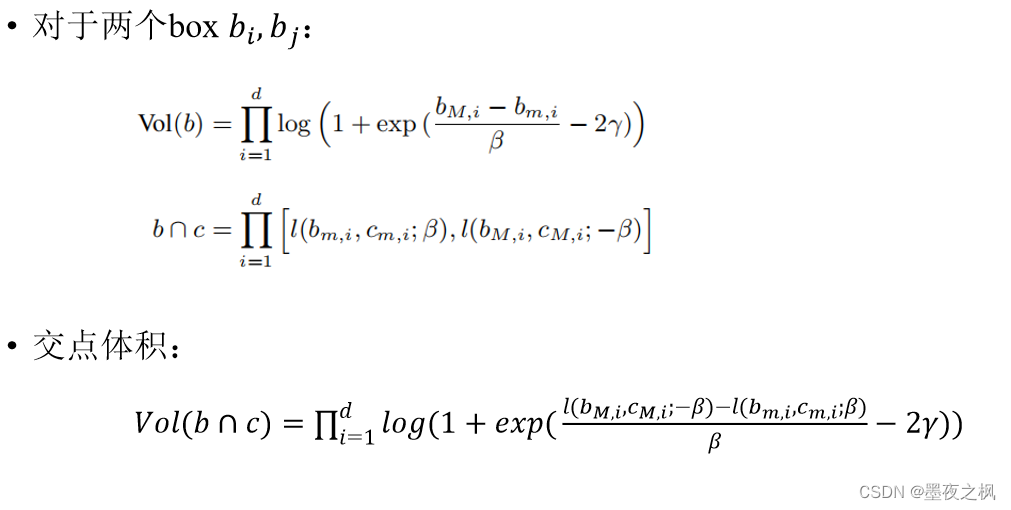
3 BERE模型

Vector模型和BERE模型之间的根本区别：BERE模型不管顺序如何，将事件映射到一致的box representation，Vector模型分别处理这两种情况，可能不会保持逻辑一致性。

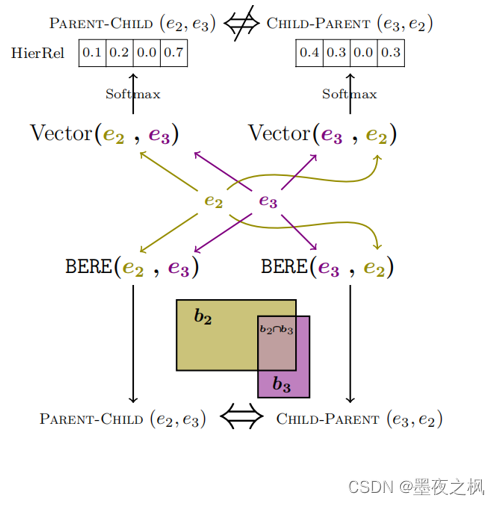
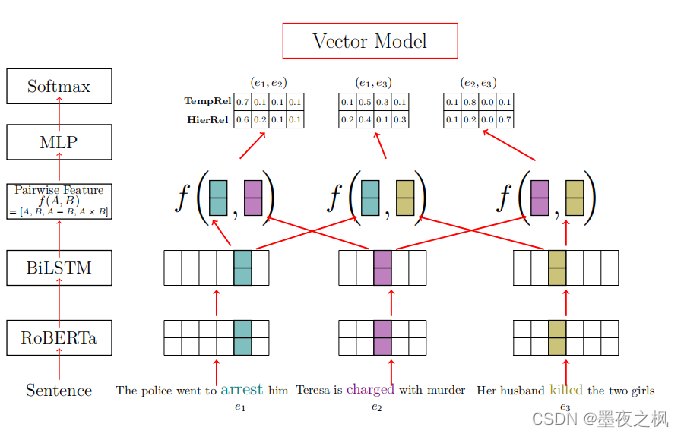
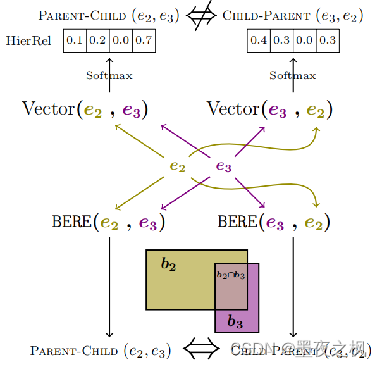
BERE模型中的事件关系是定义在box空间中使用条件概率分数进行预测：

其中，P(b_i|b_j)的值越大，越能说明box b_j包含在b_i中

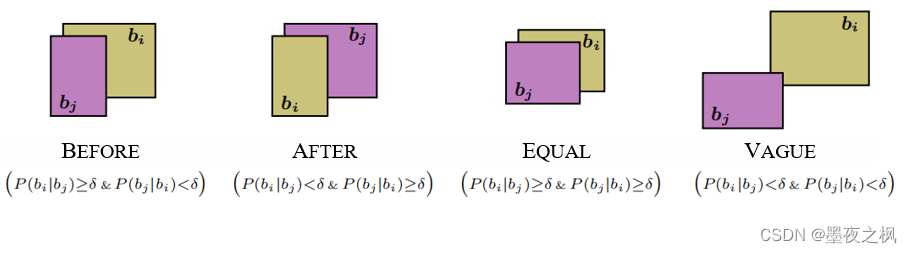
根据P(b_i|b_j)和P(b_j|b_i)进行分类得到两个事件e_i,e_j的关系r(e_i,e_j)

将标签定义为二维二元变量y^(i,j)

y₀^(i,j)=I(P(b_i|b_j)≥δ) 和 y₁^(i,j)=I(P(b_j|b_i)≥δ) 其中，I(∙)表示指示函数

BCE Loss：

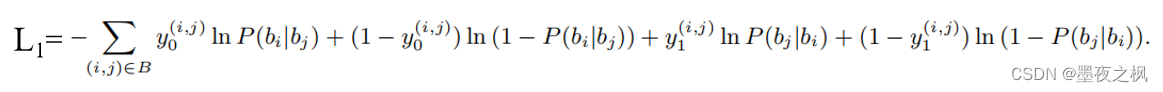
对事件关系计算二元交叉熵损失

成对损失(Pairwise Loss)：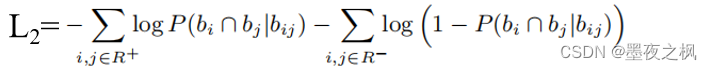

其中，R-是无关关系，如NOREL和VAGUE，而R+表示R-的补集

• 对于相关的事件对，鼓励b_i和b_j相交
• 对于无关的事件对，鼓励b_i和b_j不相交

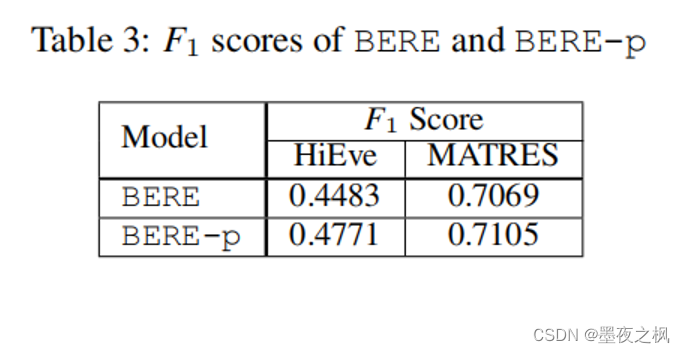
BERE：用损失L1训练的模型
BERE-p：用两个损失L1和L2组合训练的模型

4 实验

数据：HiEve、MATRES、ESL

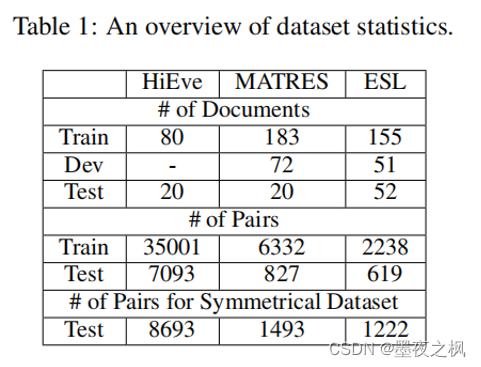
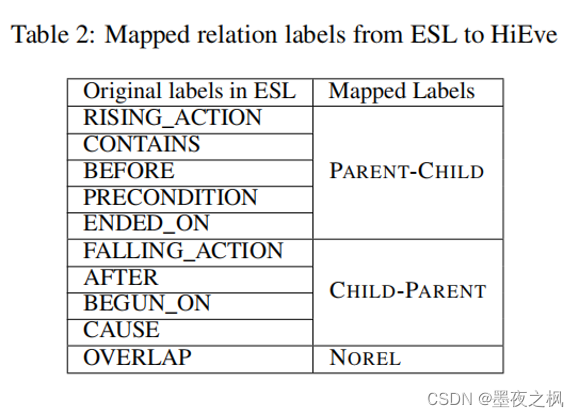
HiEve 子事件(Subevent)关系抽取：{PARENT-CHILD, CHILD-PARENT, COREF, NOREL}

MATRES 事件时序(Temporal)关系抽取：{BEFORE, AFTER, EQUAL, VAGUE}

Baseline

• Vector：RoBERTa+LSTM+MLP
• Vector-c：Vector模型+约束
• BERE：Box Embedding（仅使用L1训练）
• BERE-p：使用L1和L2组合训练

在原始和对称数据集上，分别进行单个训练和联合训练的F1 scores

• H表示HiEve, M表示MATRES, ESL表示Event StoryLine数据集
• symmetry const和conjunctive const表示反对称和连接约束违反率

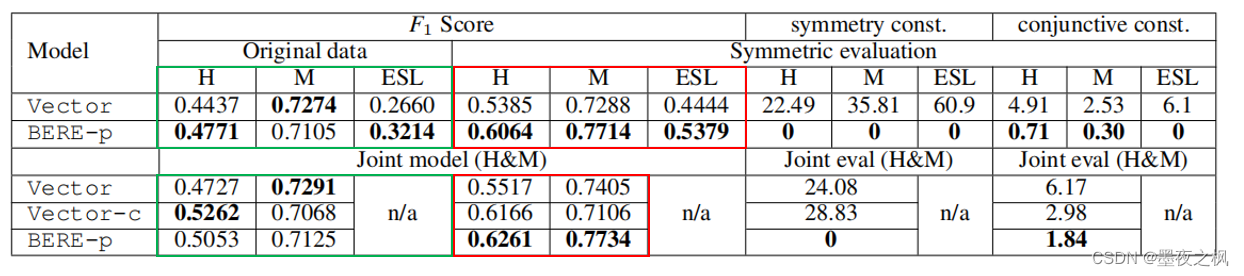
这表明BERE-p成功地捕获了反对称关系，而Vector模型难以实现

5 总结

提出了利用box embedding的事件关系抽取方法(BERE)，该方法将每个事件映射到一个box representation中，用于建模事件之间的关系。

关系类型：子事件(subevent)关系和事件时序(temporal)关系

在三个数据集(HiEve、MATRES、ESL)上实验，实验结果表明该方法不存在反对称约束违反，而且在F1 score上保持相似或较好的性能的同时显著降低的连接约束违反。