一个旅游景点,如果被带火了的话,就被称为“网红点”。大家来网红点游玩,俗称“打卡”。在各个网红点打卡的快(省)乐(钱)方法称为“攻略”。你的任务就是从一大堆攻略中,找出那个能在每个网红点打卡仅一次、并且路上花费最少的攻略。
输入格式:
首先第一行给出两个正整数:网红点的个数 N(1<N≤200)和网红点之间通路的条数 M。随后 M 行,每行给出有通路的两个网红点、以及这条路上的旅行花费(为正整数),格式为“网红点1 网红点2 费用”,其中网红点从 1 到 N 编号;同时也给出你家到某些网红点的花费,格式相同,其中你家的编号固定为 0。
再下一行给出一个正整数 K,是待检验的攻略的数量。随后 K 行,每行给出一条待检攻略,格式为:
n V1 V2 ⋯ Vn
其中 n(≤200) 是攻略中的网红点数,Vi 是路径上的网红点编号。这里假设你从家里出发,从 V1 开始打卡,最后从 Vn 回家。
输出格式:
在第一行输出满足要求的攻略的个数。
在第二行中,首先输出那个能在每个网红点打卡仅一次、并且路上花费最少的攻略的序号(从 1 开始),然后输出这个攻略的总路费,其间以一个空格分隔。如果这样的攻略不唯一,则输出序号最小的那个。
题目保证至少存在一个有效攻略,并且总路费不超过 109。
输入样例:
6 13
0 5 2
6 2 2
6 0 1
3 4 2
1 5 2
2 5 1
3 1 1
4 1 2
1 6 1
6 3 2
1 2 1
4 5 3
2 0 2
7
6 5 1 4 3 6 2
6 5 2 1 6 3 4
8 6 2 1 6 3 4 5 2
3 2 1 5
6 6 1 3 4 5 2
7 6 2 1 3 4 5 2
6 5 2 1 4 3 6
输出样例:
3
5 11
样例说明:
第 2、3、4、6 条都不满足攻略的基本要求,即不能做到从家里出发,在每个网红点打卡仅一次,且能回到家里。所以满足条件的攻略有 3 条。
第 1 条攻略的总路费是:(0->5) 2 + (5->1) 2 + (1->4) 2 + (4->3) 2 + (3->6) 2 + (6->2) 2 + (2->0) 2 = 14;
第 5 条攻略的总路费同理可算得:1 + 1 + 1 + 2 + 3 + 1 + 2 = 11,是一条更省钱的攻略;
第 7 条攻略的总路费同理可算得:2 + 1 + 1 + 2 + 2 + 2 + 1 = 11,与第 5 条花费相同,但序号较大,所以不输出。
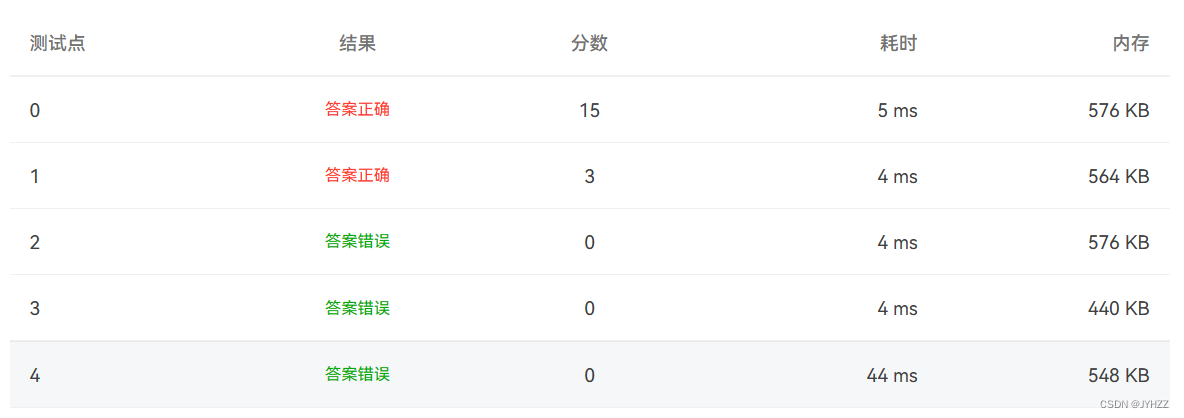
勉强过了样例
我的思路是用无向图的邻接矩阵来存储输入,邻接矩阵的值记录路费。
代码:部分正确
#include<iostream>
using namespace std;
typedef struct MGraph {
int array[200][200];
int v_num, e_num;
};
int main()
{
int n, m;
cin >> n >> m;
MGraph* mg = (MGraph*)malloc(sizeof(MGraph));
memset(mg->array, 0, sizeof(mg->array));
mg->v_num = n;
mg->e_num = m;
int a, b, c;
for (int i = 0; i < m; i++) {
cin >> a >> b >> c;
mg->array[a][b] = c;
mg->array[b][a] = c;
}
int flag = 1;
int k, temp, q;
int count = 0;
int maxcost = 999, cost = 0, maxposition = 0;
int array1[200], array2[200];//array1用来记录我们访问过的景点,array2用来记录我们的路线
cin >> k;
for (int i = 0; i < k; i++) {
flag = 1;
cost = 0;
fill(array1, array1 + n, 0);
cin >> temp;
if (temp < n) {//如果给出的点少于景点数,肯定不能全访问
flag = 0;
}
array2[0] = 0;//0代表是家
int p;
for (int j = 1; j <= temp; j++) {
cin >> p;
array1[p]++;
if (array1[p] > 1) {//如果这个景点访问了两次及以上
flag = 0;//不符合要求
}
else {
array2[j] = p;
}
}
array2[temp + 1] = 0;//最后是回家
for (int j = 0; j <= temp && flag; j++) {
if (mg->array[array2[j]][array2[j + 1]] == 0) {
flag = 0;
break;
}
cost += mg->array[array2[j]][array2[j + 1]];
}
if (flag) {
count++;
if (cost < maxcost) {
maxcost = cost;
maxposition = i + 1;
}
}
}
cout << count << endl;
cout << maxposition << " " << maxcost << endl;
return 0;
}
因为没有判断所有景点是否都访问过了,所以测试点3没过:
for (int j = 1; j <= temp; j++) {
cin >> p;
array1[p]++;
if (array1[p] > 1) {
flag = 0;
}
else {
array2[j] = p;
}
}
array2[temp + 1] = 0;
//这个是新加的
for (int i = 1; i < n; i++) {
if (array1[i] == 0) {
flag = 0;
}
}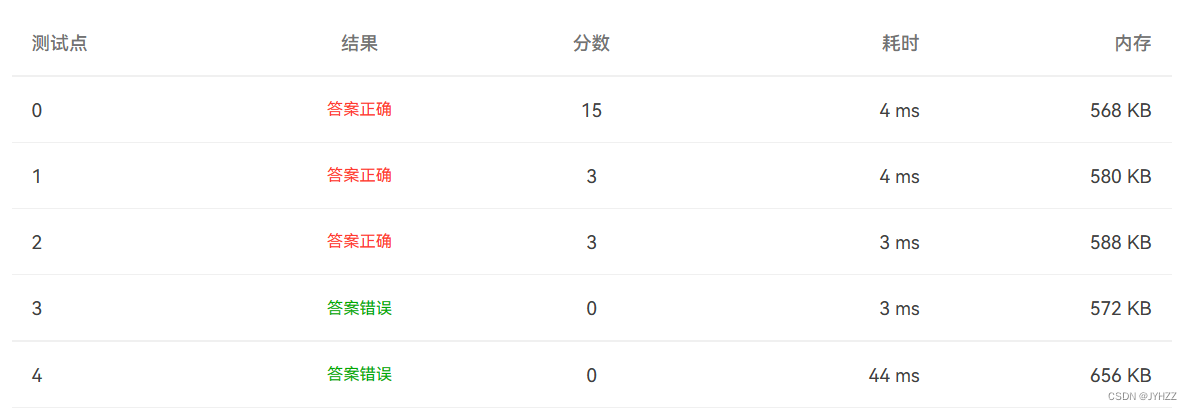
然后是因为这里,测试点4没过
原来是这样:
fill(array1, array1 + n, 0); 修改后:
fill(array1, array1+200, 0); 最后的代码:只剩下测试点5没过了
#include<iostream>
#include<string.h>
#include<string>
#include<queue>
#include<stack>
using namespace std;
typedef struct MGraph {
int array[200][200];
int v_num, e_num;
};
int main()
{
int n, m;
cin >> n >> m;
MGraph* mg = (MGraph*)malloc(sizeof(MGraph));
memset(mg->array, 0, sizeof(mg->array));
mg->v_num = n;
mg->e_num = m;
int a, b, c;
for (int i = 0; i < m; i++) {
cin >> a >> b >> c;
mg->array[a][b] = c;
mg->array[b][a] = c;
}
int flag = 1;
int k, temp, q;
int count = 0;
int maxcost = 2000000000, cost = 0, maxposition = 0;
int array1[200], array2[200];//array1用来记录我们访问过的景点,array2用来记录我们的路线
cin >> k;
for (int i = 0; i < k; i++) {
flag = 1;
cost = 0;
fill(array1, array1+200, 0);
fill(array2, array2 +200, 0);
cin >> temp;
if (temp < n) {//如果给出的点少于景点数,肯定不能全访问
flag = 0;
}
array2[0] = 0;//0代表是家
int p;
for (int j = 1; j <= temp; j++) {
cin >> p;
array1[p]++;
if (array1[p] > 1) {//如果这个景点访问了两次及以上
flag = 0;//不符合要求
}
else {
array2[j] = p;
}
}
array2[temp + 1] = 0;//最后是回家
for (int j = 0; j <= temp && flag; j++) {
if (mg->array[array2[j]][array2[j + 1]] == 0) {
flag = 0;
}
cost += mg->array[array2[j]][array2[j + 1]];
}
if (flag) {
count++;
if (cost < maxcost) {
maxcost = cost;
maxposition = i + 1;
}
}
}
cout << count << endl;
cout << maxposition << " " << maxcost << endl;
return 0;
}