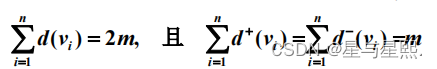目录
例
相关概念
握手定理
例1
图的度数列
例
无向图的连通性
无向图的连通度
例2
例3
有向图D如图所示,求 A, A2, A3, A4,并回答诸问题:
中间有几章这里没有写,感兴趣可以自己去学,组合数学跟高中差不多,这里也没写了,绝不是因为作者懒!
定义9 .1 无向图 G = < V , E >, 其中(1) V ≠ ∅ 为顶点集,元素称为 顶点(2) E 为 V & V 的多重集,其元素称为无向边,简称 边
例
G = <V,E>为无向图
V = { v 1, v2, v3,v4,v5}E = {( v 1 , v 1 ), ( v 1 , v 2 ), ( v 2 , v 3 ), ( v 2 , v 3 ), ( v 2 , v 5 ), ( v 1 , v 5 ), ( v 4 , v 5 )}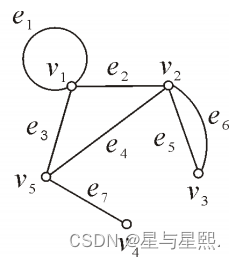
定义9 .2 有向图 D =< V , E >, 只需注意 E 是 V × V 的多重子集
相关概念
1. 图① 可用 G 泛指图(无向的或有向的)② V ( G ), E ( G ), V ( D ), E ( D )③ n 阶图2. 有限图3. n 阶零图与平凡图4. 空图 —— ∅5. 用 e k 表示无向边或有向边6. 顶点与边的关联关系① 关联、关联次数② 环③ 孤立点7. 顶点之间的相邻与邻接关系8. 邻域与关联集① v ∈ V ( G ) ( G 为无向图 )v的邻域 N(v)={u|u∈V(G)∧(u,v)∈E(G)∧u≠v}v的闭邻域(v)=N(v)∪{v}
v的关联集 I(v)={e|e∈E ( G ) ∧ e 与 v 关联 }② v ∈ V ( D ) ( D 为有向图 )v的后继元集(v)={u|u∈V(D) ∧<v,u>∈E(D) ∧u≠v}
v的先驱元集(v)= {u|u∈V(D) ∧<u,v>∈E(D) ∧u≠v}
v的邻域(v)=
(v)∪
(v)
v的闭邻域(v)=
(v)∪{v}
9. 标定图与非标定图10. 基图
定义9 .3(1) 无向图中的平行边及重数(2) 有向图中的平行边及重数 注意方向性(3) 多重图(4) 简单图
定义9 .4(1) 设 G =< V , E > 为无向图 , ∀ v ∈ V , d ( v )—— v 的度数 , 简称度(2) 设 D =< V , E > 为有向图∀ v ∈ Vd + ( v )—— v 的出度d − ( v )—— v 的入度d ( v )—— v 的度或度数(3)∆ ( G )最大度δ ( G )最小度(4)∆ + ( D )最大出度δ + ( D )最小出度∆ − ( D )最大入度δ − ( D )最小入度(5) 奇顶点度与偶度顶点
握手定理
定理9.1 设G=<V,E>为任意无向图,V={v1,v2,…,vn}, |E|=m, 则
G 中每条边 ( 包括环 ) 均有两个端点,所以在计算 G 中各顶点 度数之和时,每条边均提供 2 度, m 条边共提供 2 m 度
定理9.2 设D=<V,E>为任意有向图,V={v1,v2,…,vn}, |E|=m, 则
总度数为边数的两倍,入度和出度都等于边数
例1
无向图 G 有 16 条边, 3 个 4 度顶点, 4 个 3 度顶点,其余 顶点度数均小于 3 ,问 G 的阶数 n 为几?解本题的关键是应用握手定理设除 3 度与 4 度顶点外还有 x 个顶点 v 1 , v 2 , …, v x则d ( v i ) ≤ 2 , i =1, 2, …, x于是得不等式32 ≤ 24+2 x得 x ≥ 4阶数 n ≥ 4+4+3=11
图的度数列
V ={ v 1 , v 2 , …, v n } 为无向图 G 的顶点集,称 d ( v 1 ), d ( v 2 ), …, d ( v n ) 为 G 的 度数列V ={ v 1 , v 2 , …, v n } 为有向图 D 的顶点集D 的 度数列 : d ( v 1 ), d ( v 2 ), …, d ( v n )D 的 出度列 : d + ( v 1 ), d + ( v 2 ), …, d + ( v n )D 的 入度列 : d − ( v 1 ), d − ( v 2 ), …, d − ( v n )非负整数列 d =( d 1 , d 2 , …, d n ) 是 可图化的 ,是 可简单图化 的度数列=入度列+出度列,对应元素例
度数列={3,2,3,2}
出度列={2,1,2,1}
则求入读列
{1,1,1,1}
定义9 .5 设 G 1 =< V 1 , E 1 >, G 2 =< V 2 , E 2 > 为两个无向图 ( 两个有向 图 ) ,若存在双射函数 f : V 1 → V 2 , 对于 v i , v j ∈ V 1 , ( v i , v j ) ∈ E 1 当且仅当 ( f ( v i ), f ( v j )) ∈ E 2 ( < v i , v j > ∈ E 1 当且仅当 < f ( v i ), f ( v j )> ∈ E 2 ) 并且 , ( v i , v j ) ( < v i , v j > )与 ( f ( v i ), f ( v j )) ( < f ( v i ), f ( v j )> )的重数相 同,则称 G 1 与 G 2 是 同构 的,记作 G 1 ≅ G 2
图之间的同构关系具有自反性、对称性和传递性能找到多条同构的必要条件,但它们全不是充分条件:① 边数相同,顶点数相同② 度数列相同③ 对应顶点的关联集及邻域的元素个数相同 等若破坏必要条件,则两图不同构判断两个图同构是个难题
定义9.6
(1) n ( n ≥ 1) 阶无向完全图 —— 每个顶点与其余顶点均相邻的 无向简单图,记作 K n简单性质:边数m = n ( n − 1) /2∆ = δ = n − 1(2) n ( n ≥ 1) 阶 有向完全图 —— 每对顶点之间均有两条方向相 反的有向边的有向简单图简单性质:m = n ( n − 1)∆ = δ = 2( n − 1)∆ + = δ + = n − 1(3) n ( n ≥ 1) 阶 竞赛图 —— 基图为 K n 的有向简单图简单性质:边数m = n ( n 2 − 1)∆ = δ = n − 1
定义9.7 n 阶k正则图——∆=δ=k 的无向简单图
简单性质:边数(由握手定理得)
m=nk/2
定义9 .8 G =< V , E >, G ′ =< V ′ , E ′ >(1) G ′⊆ G —— G ′ 为 G 的 子图 , G 为 G ′ 的 母图(2) 若 G ′⊆ G 且 V ′ = V ,则称 G ′ 为 G 的 生成子图(3) 若 V ′⊂ V 或 E ′⊂ E ,称 G ′ 为 G 的 真子图(4) V ′ ( V ′⊂ V 且 V ′≠∅ )的 导出子图 ,记作 G [ V ′ ](5) E ′ ( E ′⊂ E 且 E ′≠∅ )的 导出子图 ,记作 G [ E ′ ]
定义9 .9 设 G =< V , E > 为 n 阶无向简单图,以 V 为顶点集,以 所有使 G 成为完全图 K n 的添加边组成的集合为边集的图, 称为 G 的 补图 ,记作 G若G≅ G , 则称G是自补图.
定义9 .10 给定图 G =< V , E > (无向或有向的), G 中 顶点与 边的交替序列 Γ = v 0 e 1 v 1 e 2 … e l v l , v i − 1 , v i 是 e i 的端点(1) 通路与回路: Γ 为 通路 ;若 v 0 = v l , Γ 为 回路 , l 为 回路长 度(2) 简单通路与回路:所有边各异, Γ 为 简单通路 ,又若 v 0 = v l , Γ 为 简单回路(3) 初级通路 ( 路径 ) 与初级回路 ( 圈 ) : Γ 中所有顶点各异,则 称 Γ 为 初级通路 ( 路径 ) ,又若除 v 0 = v l ,所有的顶点各不相 同且所有的边各异,则称 Γ 为 初级回路 ( 圈 )(4) 复杂通路与回路:有边重复出现
定理9 .3 在 n 阶图 G 中,若从顶点 v i 到 v j ( v i ≠ v j )存在通路, 则从 v i 到 v j 存在长度小于或等于 n − 1 的通路定理9 .4 在一个 n 阶图 G 中,若存在 v i 到自身的回路,则一 定存在 v i 到自身长度小于或等于 n 的回路
无向图的连通性
(1) 顶点之间的连通关系: G =< V , E > 为无向图① 若 v i 与 v j 之间有通路,则 v i ∼ v j② ∼ 是 V 上的等价关系 R ={< u , v >| u , v ∈ V 且 u ∼ v }(2) G 的连通性与连通分支① 若 ∀ u , v ∈ V , u ∼ v ,则称 G 连通② V / R ={ V 1 , V 2 ,…, V k } ,称 G [ V 1 ], G [ V 2 ], …, G [ V k ] 为 连通分 支 ,其个数 p ( G )= k ( k ≥ 1)k =1 , G 连通(3) 短程线与距离① u 与 v 之间的 短程线 : u ∼ v , u 与 v 之间长度最短的通路② u 与 v 之间的 距离 : d ( u , v )—— 短程线的长度③ d ( u , v ) 的性质:d ( u , v ) ≥ 0, u ≁ v 时 d ( u , v )= ∞d ( u , v )= d ( v , u )d ( u , v )+ d ( v , w ) ≥ d ( u , w )
无向图的连通度
删除顶点及删除边G − v —— 从 G 中将 v 及关联的边去掉G − V ′ —— 从 G 中删除 V ′ 中所有的顶点G − e —— 将 e 从 G 中去掉G − E ′ —— 删除 E ′ 中所有边点割集与边割集点割集与割点
定义9.11 G=<V,E>, V′⊂V
V ′ 为 点割集 —— p ( G − V ′ )> p ( G ) 且有极小性v 为 割点 ——{ v } 为点割集定义9 .12 G =< V , E >, E ′⊆ EE ′ 是 边割集 —— p ( G − E ′ )> p ( G ) 且有极小性e 是 割边 (桥) ——{ e } 为边割集
点割集和边割集的两个要求
删去集合里的所有边或点,会增加连通分支
删去集合中的子集不会增加连通分支
例2
点割集 {v5},{v6},{v1,v4}
割点 v5,v6
边割集 {e7},{e8},{e1,e2},{e1,e4,e6},{e2,e3,e9},{e1,e3,e9},{e2,e4,e6},{e3,e4,e5},{e1,e3,e5,e6},{e2,e4,e5,e9},{e1,e4,e5,e9},{e2,e3,e5,e9}
割边(桥) e7,e8
定义9 .13 D =< V , E > 为有向图v i → v j ( v i 可达 v j ) —— v i 到 v j 有通路v i ↔ v j ( v i 与 v j 相互可达)性质→ 具有自反性 ( v i → v i ) 、传递性↔ 具有自反性、对称性、传递性v i 到 v j 的短程线与距离类似于无向图中,只需注意距离表示法的不同( 无向图中 d ( v i , v j ) ,有向图中 d < v i , v j >) 及 d < v i , v j > 无对称性
定义9.14 D=<V,E>为有向图
D 弱连通 ( 连通 )—— 基图为无向连通图D 单向连通 —— ∀ v i , v j ∈ V , v i → v j 或 v j → v iD 强连通 —— ∀ v i , v j ∈ V , v i ↔ v j易知,强连通 ⇒ 单向连通 ⇒ 弱连通
判别法定理9 .4 D 强连通当且仅当 D 中存在经过每个顶点至少一次 的回路定理9 .5 D 单向连通当且仅当 D 中存在经过每个顶点至少一 次的通路
定义9.15 设 G =< V , E > 为一个无向图,若能将 V 分成 V 1 和 V 2 ( V 1 ∪ V 2 = V , V 1 ∩ V 2 = ∅ ) ,使得 G 中的每条边的两个端点都是 一个属于 V 1 ,另一个属于 V 2 ,则称 G 为 二部图 ( 或称 二分图 、 偶图 等 ) ,称 V 1 和 V 2 为 互补顶点子集 ,常将二部图 G 记为 < V 1 , V 2 , E > 又若 G 是简单二部图, V 1 中每个顶点均与 V 2 中所有的顶点相 邻 则称 G 为 完全二部图 ,记为 K r , s ,其中 r =| V 1 | , s =| V 2 |注意, n 阶零图为二部图完全二部图V1集合每个点都与V2集合中每个点相连
定理9.6 无向图G=<V,E>是二部图当且仅当G中无奇圈
定义9 .16 无向图 G =< V , E > , | V |= n , | E |= m ,令 m ij 为 v i 与 e j 的关联次数,称 ( m ij ) n × m 为 G 的 关联矩阵 ,记为 M ( G )
定义9 .17 有向图 D =< V , E > ,令 则称 ( m ij ) n × m 为 D 的 关联矩阵 ,记为 M ( D )
定义9 .18 设有向图 D =< V , E >, V ={ v 1 , v 2 , …, v n }, E ={ e 1 , e 2 , …, e m }, 令为顶点 v i 邻接到顶点 v j 边的条数,称为 D 的 邻接矩 阵 ,记作 A ( D ) ,或简记为 A
定理9.7 设 A为有向图 D 的邻接矩阵,V={v1, v2, …, vn}为顶点集,则 A 的 l 次幂 Al (l≥1)中元素
为D中vi 到vj 长度为 l 的通路数,其中
为vi 到自身长度为 l 的回路数,而
为D中长度为 l 的通路总数,
为D 中长度为 l 的回路总数
例3
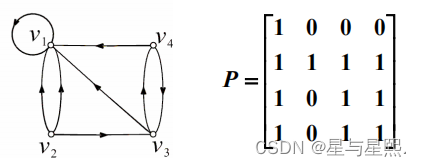
有向图D如图所示,求 A, A2, A3, A4,并回答诸问题:
(1) D 中长度为 1, 2, 3, 4 的通路各有多少条?其中回路分别为多 少条?(2) D 中长度小于或等于 4 的通路为多少条?其中有多少条回路?
(1)D 中长度为 1 的通路为 8 条,其中有 1 条是回路D 中长度为 2 的通路为 11 条,其中有 3 条是回路D 中长度为 3 和 4 的通路分别为 14 和 17 条,回路分别 为 1 与 3 条(2)D 中长度小于等于 4 的通路为 50 条,其中有 8 条是回路下标(i,i)的数的和为回路总数,(i,j)的数的和为通路总数
定义9.19 设D=<V,E>为有向图. V={v1, v2, …, vn}, 令
称 (pij)n×n 为D的可达矩阵,记作P(D),简记为由于∀vi ∈V,vi ↔vi ,所以P(D)主对角线上的元素全为1
由定义不难看出, D 强连通当且仅当P(D)为全1矩阵
下图所示有向图 D 的可达矩阵为