梯度下降

1.梯度下降算法

之前可以使用穷举的方法逐个测试找使损失函数最小的点，但当数据过多时，维度过高，会使穷举变得非常困难，因此需要优化，梯度下降法就是其中一种优化方式。
要找到最小值的点，可以让点沿着下降最快的方向移动，梯度的负方向就是下降最快的方向，w随之更新。

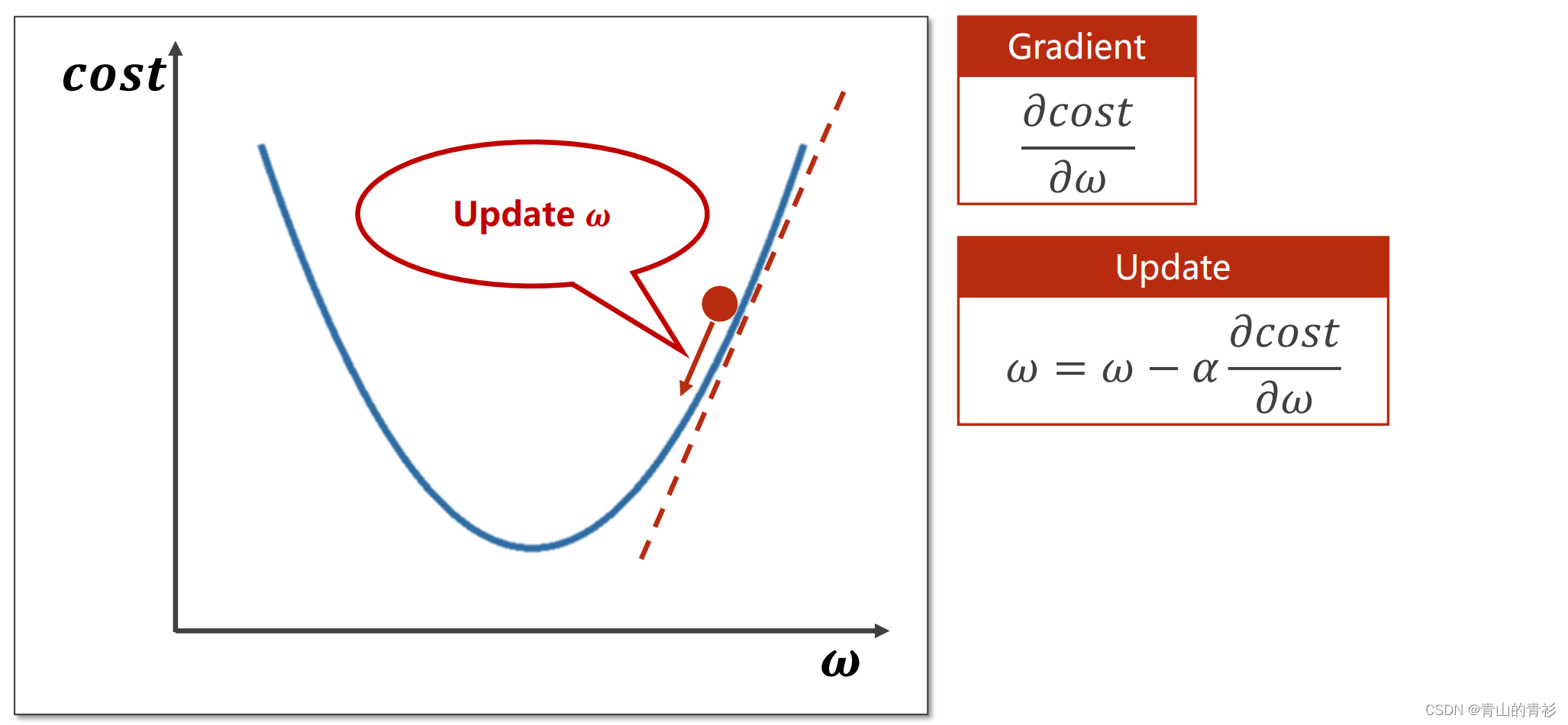
图中公式的α值代表学习率，通常是一个很小的数，代表步长。

这样的计算存在两个问题，如下图：

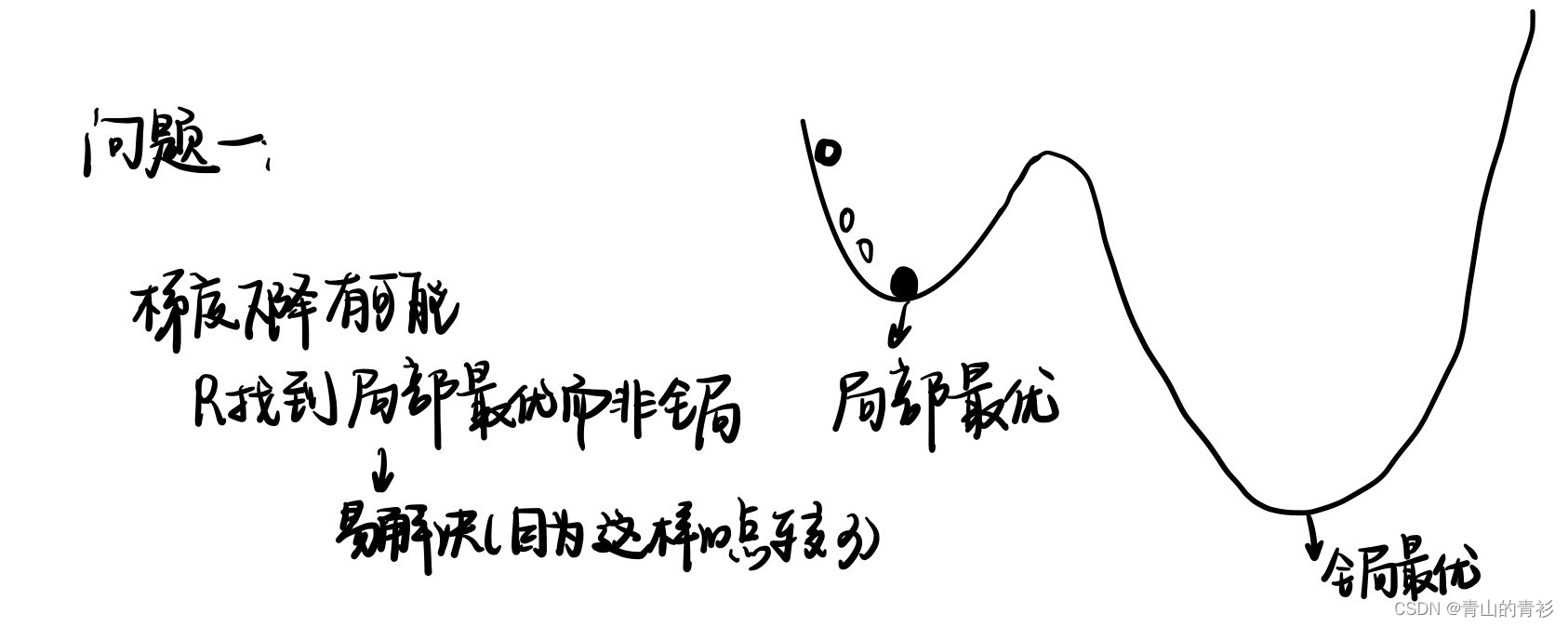
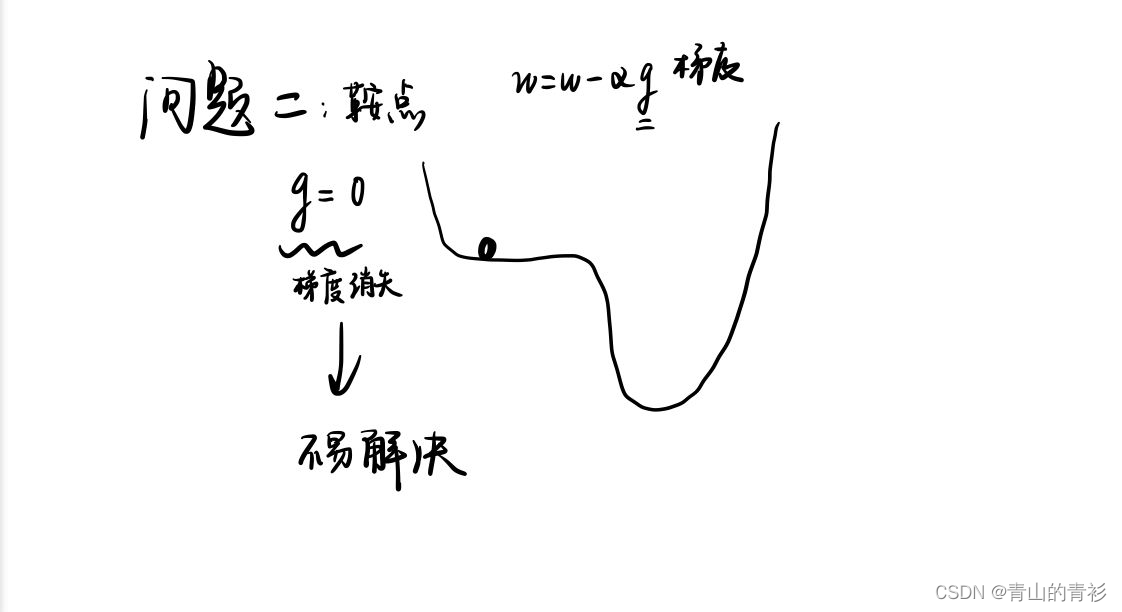
本例中的梯度计算结果如下图：

实现代码

import numpy as np               # 导入必须的包
import matplotlib.pyplot as plt

# 1.建立线性模型
x_data = [1.0, 2.0, 3.0]  # 数据集整理
y_data = [2.0, 4.0, 6.0]

w = 1.0                  # 给权重w一个初始值

def forward(x):      # 定义线性模型，计算y_hat
    return x * w

def cost(xs,ys):        # 定义mse
    cost = 0
    for x,y in zip(xs,ys):
        y_pred = forward(x)   #计算y_hat
        cost += (y_pred - y) ** 2 # 求平方并累加
    return cost / len(xs)  # 求均值

def gradient(xs,ys):
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

print("Predict (before training)",4 ,forward(4))

for epoch in range(100):            # 进行100轮训练
    cost_val = cost(x_data,y_data)      # 计算损失值
    grad_val = gradient(x_data,y_data)
    w -= 0.01 * grad_val            # 学习率取0.01
    print("Epoch",epoch, "w=",w ,"loss=", cost_val)  #打印日志

print("Predict (after training)",4 ,forward(4))

2.随机梯度下降

cost：N个求平均->loss：从N个随机挑一个

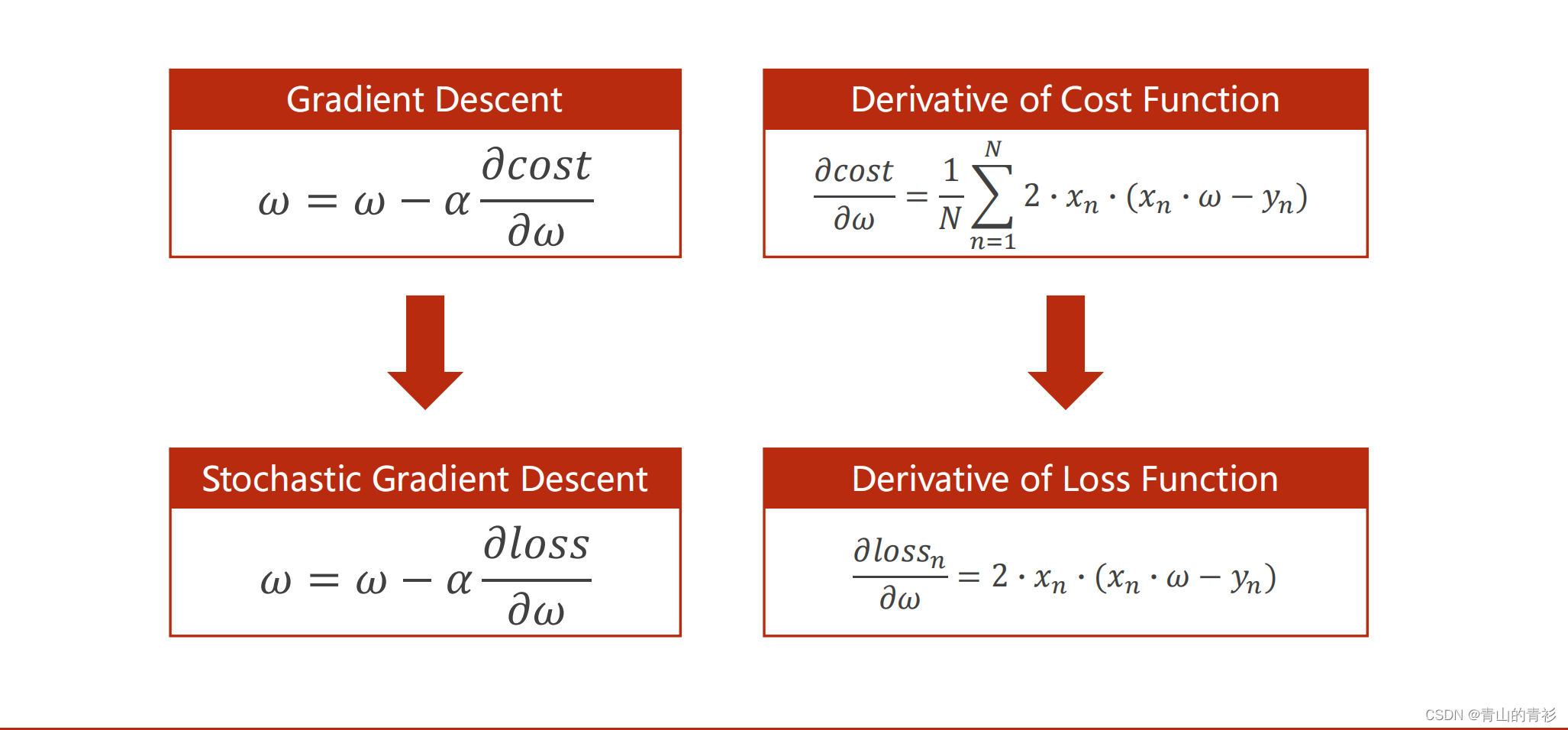
原因如下图：

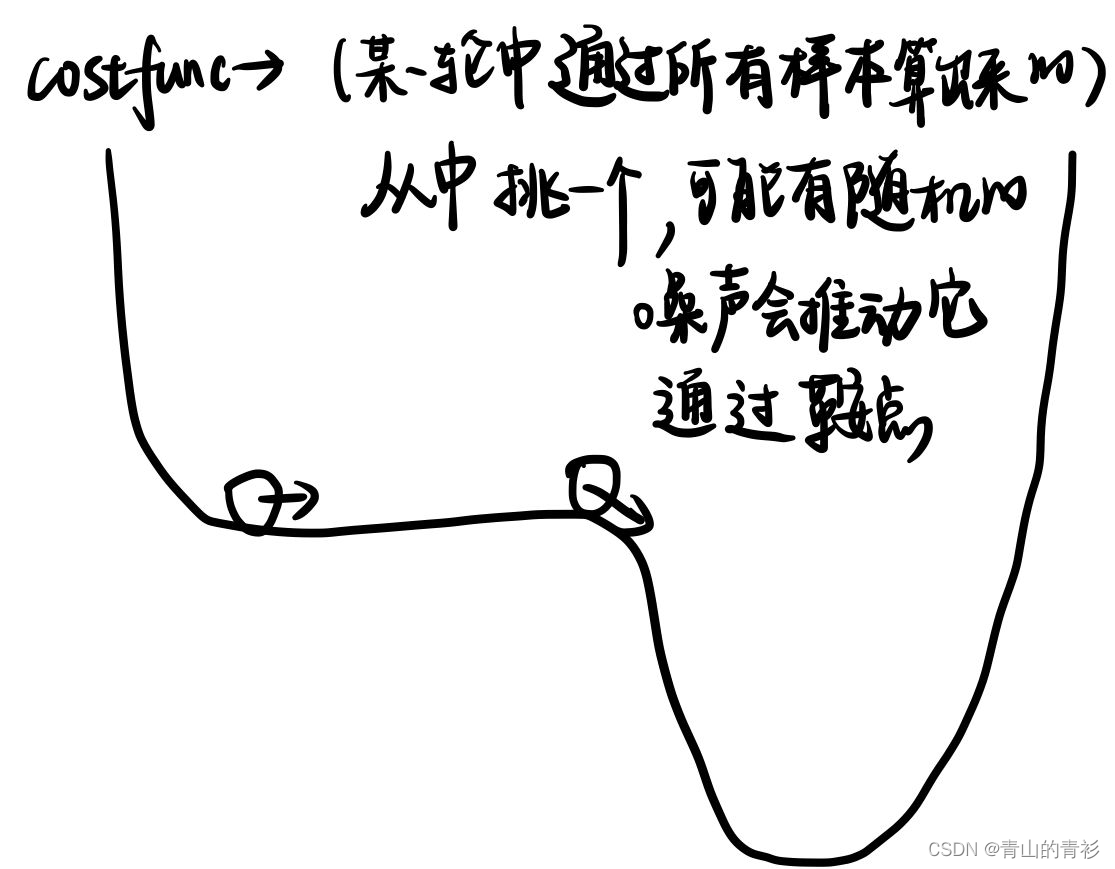
实现代码

# 1.建立线性模型
x_data = [1.0, 2.0, 3.0]  # 数据集整理
y_data = [2.0, 4.0, 6.0]

w = 1.0                  # 给权重w一个初始值

def forward(x):      # 定义线性模型，计算y_hat
    return x * w

def loss(x,y):          # 求其中一个样本的损失值
    y_pred = forward(x)
    return (y_pred - y) ** 2

def gradient(x,y):      # 求梯度
    return 2 * x * (x * w - y)

print("Predict (before training)",4 ,forward(4))	# 训练前

for epoch in range(100):              # 进行100轮训练
    print(f"这是第{epoch}轮")
    for x,y in zip(x_data, y_data):	  # 以下是w的更新，并不随机！
        grad = gradient(x,y)          # 对一个样本求梯度，注意这里没有随机性！不符合随机梯度下降，只是按顺序选了其中一个！
        w = w - 0.01 * grad           # 进行更新，学习率取0.01
        l = loss(x,y)
        print("\tgrad", x, y, w, grad)

print("Predict (after training)",4 ,forward(4))     # 训练后

3.小批量随机梯度下降

随机梯度下降并行度较差，时间复杂度高，但是性能较好。
梯度下降并行度更好，时间复杂度低，但是性能较差。（实话讲这里没听懂老师说的原因，只知道结论了，先记录下来）
因此，引入小批量随机梯度下降（mini-batch），给数据分组，组内使用梯度下降，组间使用随机梯度下降。