通过万岁！！！

• 题目：这个题目比较复杂，就是给你一个坐标轴，然后让你以0,0为中心选择一个边长为整数的正方形，使得正方形中所有点坐标的绝对值之和要大于给定的neededApples。但是我们需要输出的是这个正方形的周长。
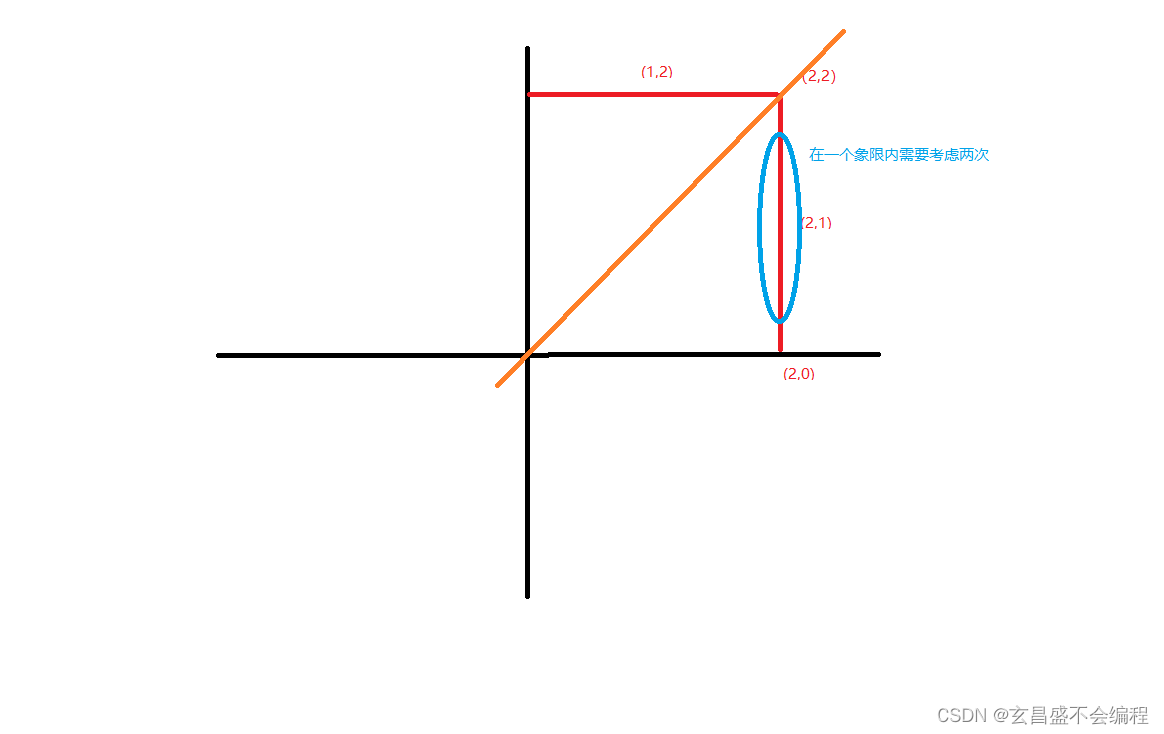
• 基础思路：我们首先把思路定在第一象限，然后坐标轴x的长度8，则得到最后要的周长。我们以x的长度为2进行举例，并且我们只考虑周长上的点，那么我们第一象限需要考虑的点就是(1,2)、(2,2)、(2,1)、(2,0)。需要注意的是(0,2)和(2,0)我们只需要考虑一个就好了。然后我们沿着第一象限正方形的对角线（y=x）对正方形分成两部分，然后只考虑垂直于x轴的这条边，上面的点包括(2,2)、(2,1)、(2,0)，我们发现在第一象限中，(2,2)和(2,0)我们只需要计算一次，但是(2,1)这种情况我们需要计算两次。也就是说，在第一象限中，一条边上的点，头尾我们只需要计算一次就好了，但是中间的我们需要计算两次。以垂直于x轴的边来说，正方形的变成为i，则(i,0)和(i,i)我们只需要计算一次，(i,k)则需要计算两次。然后最后将这个结果4，则得到边长为2*i时正方形边上的苹果个数。剩下的就是只需要把上次的加上，然后看一下是不是大于neededApples就好了。上面的代码就得到的第一版，但是这个代码超时了。写完以后就发现，其实可以优化的。
  
• 优化思路：其实里面的for循环我们可以优化的，(i,k)的点我们需要计算2次，一共由i-1个点。那么针对x坐标来说有i*(i-1)2个苹果，对于y坐标来说，我们有(1+2+…+(i-1))2个苹果，然后再加上首位两个i2+i，然后再4个象限，最终换算出来的结果是12ii。所以while中的代码最终可以优化为i++以后，sum+=12ii。
• 技巧：数学

java代码——基础思路

class Solution {
    public long minimumPerimeter(long neededApples) {
        long i = 1, sum = 12;
        while (sum < neededApples) {
            i++;
            sum += (i + i) * 4;// (i,i)这个点
            sum += i * 4;// (i,0)这个点
            for (int k = 1; k < i; k++) {
                sum += (i + k) * 2 * 4;// 中间的(i,k)的点
            }
        }
        return i * 8;
    }
}

java代码——优化思路

class Solution {
    public long minimumPerimeter(long neededApples) {
        long i = 1, sum = 12;
        while (sum < neededApples) {
            i++;
            sum += 12 * i * i;
        }
        return i * 8;
    }
}

• 总结：题目不是特别难，但是要发现这里面的规律，画画图其实就出来了。