如果您的服务器没有图形界面(GUI),您可以通过命令行(终端)来安装和配置Tomcat、JDK和MySQL等软件。以下是在没有图形界面GHome的 Linux 系统上安装这些软件的基本步骤:
对于CentOS Stream 9,您可以按照以下步骤在命令行上安装Tomcat、JDK 和 MySQL 数据库:
1. 安装JDK:
sudo dnf update
安装OpenJDK或Oracle JDK。对于OpenJDK 11:
sudo dnf install java-11-openjdk-devel
验证安装:
java -version
如果你命令行不熟悉,或者命令行安装容易出错的话,我建议你要安装的话,可以用SSH远程连接linux服务器工具,比如XShell 或者FinalShell 。
首先下载安装ssh软件,这里用FinalShell举例
在linux 服务器上如下 使用命令查看 linux本机ip 如果ens33 没有下面的话,你要设置网卡,这个自行百度吧
ip addr
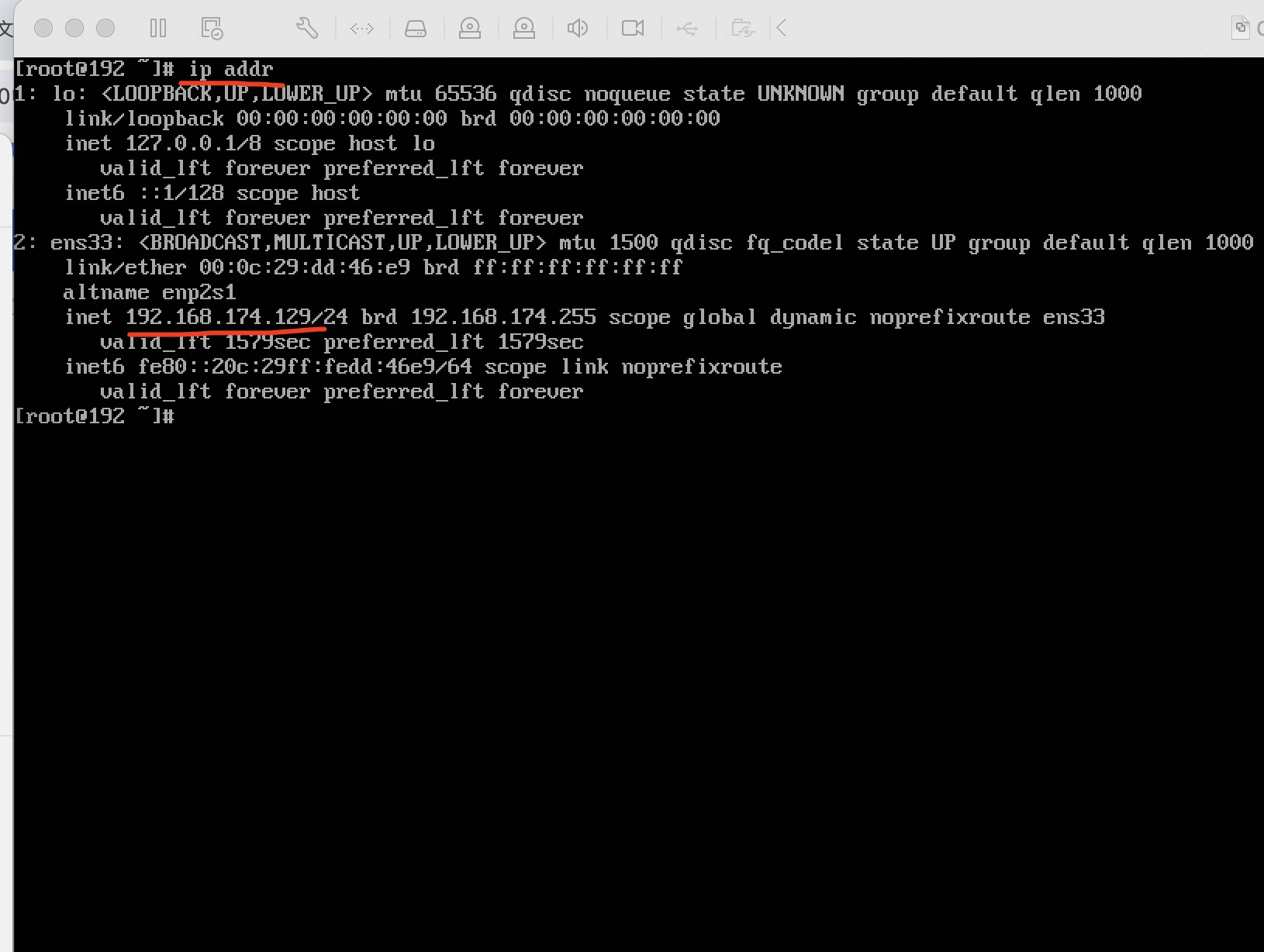
找到上边的ip 192.168.174.129 填入主机输入框 不需要后面的/24,端口号默认22不用改变。
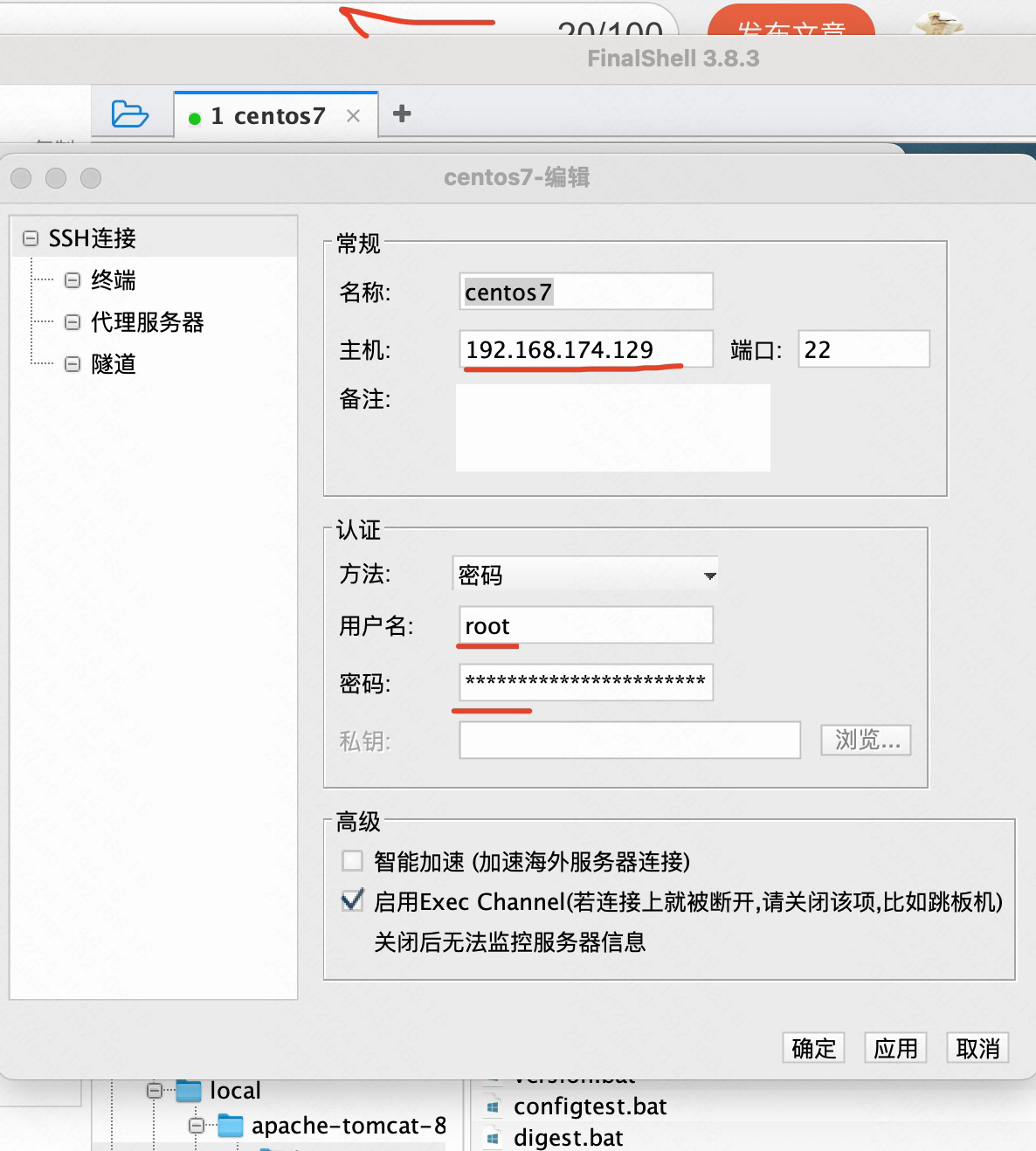
然后输上ip 就可以连接成功了,然后使用finalShell 自带的上传按钮,进行上传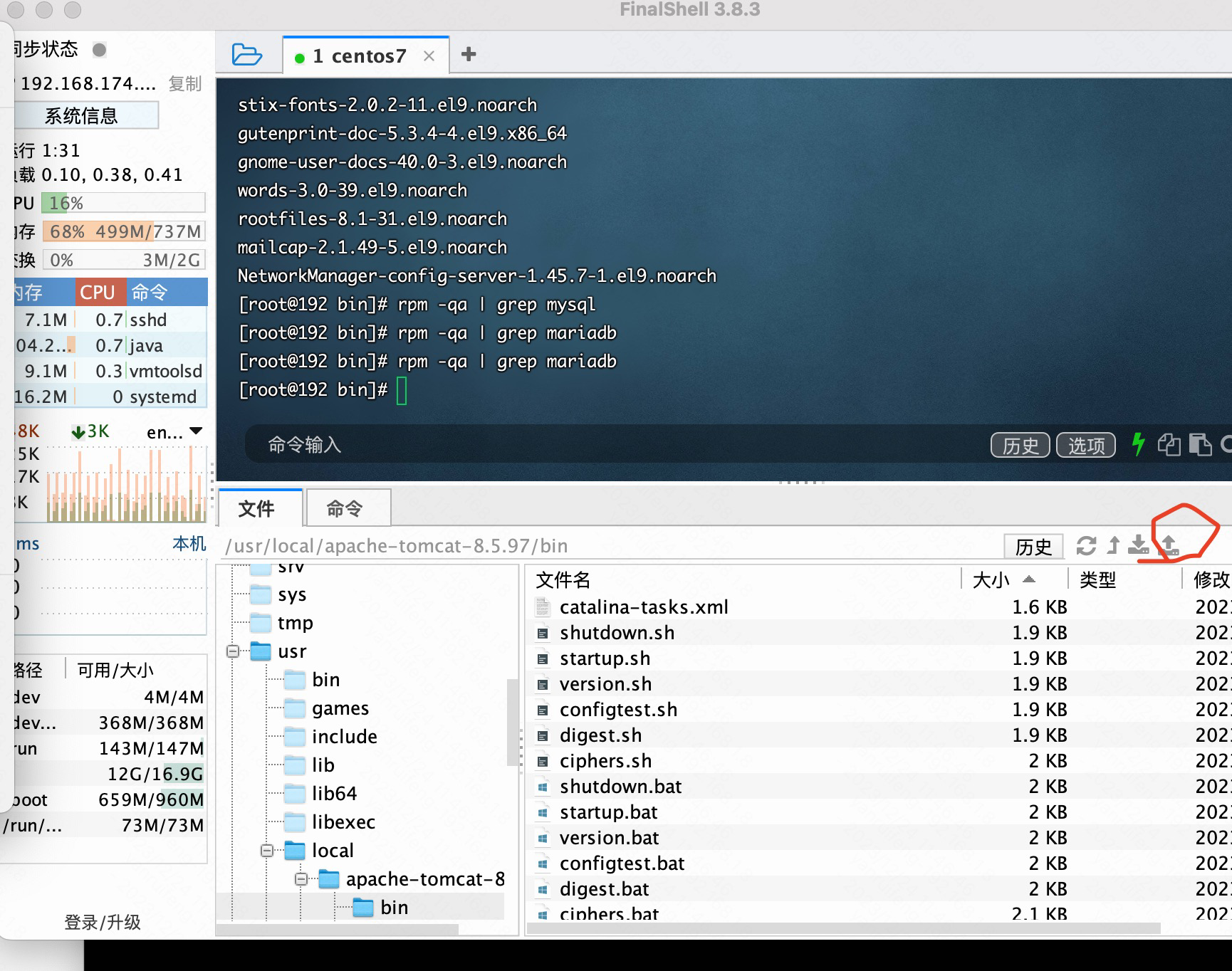
上传完成后,目前我存放的是linux /根目录
然后我想把他解压到指定目录的话
就需要 linux如下命令
tar -zxvf tomcat二进制发布包(以.gz结尾)的文件名 -C /usr/local
然后就会解压 ,解压完成后就会在指定usr/local看到apache-tomcat文件夹
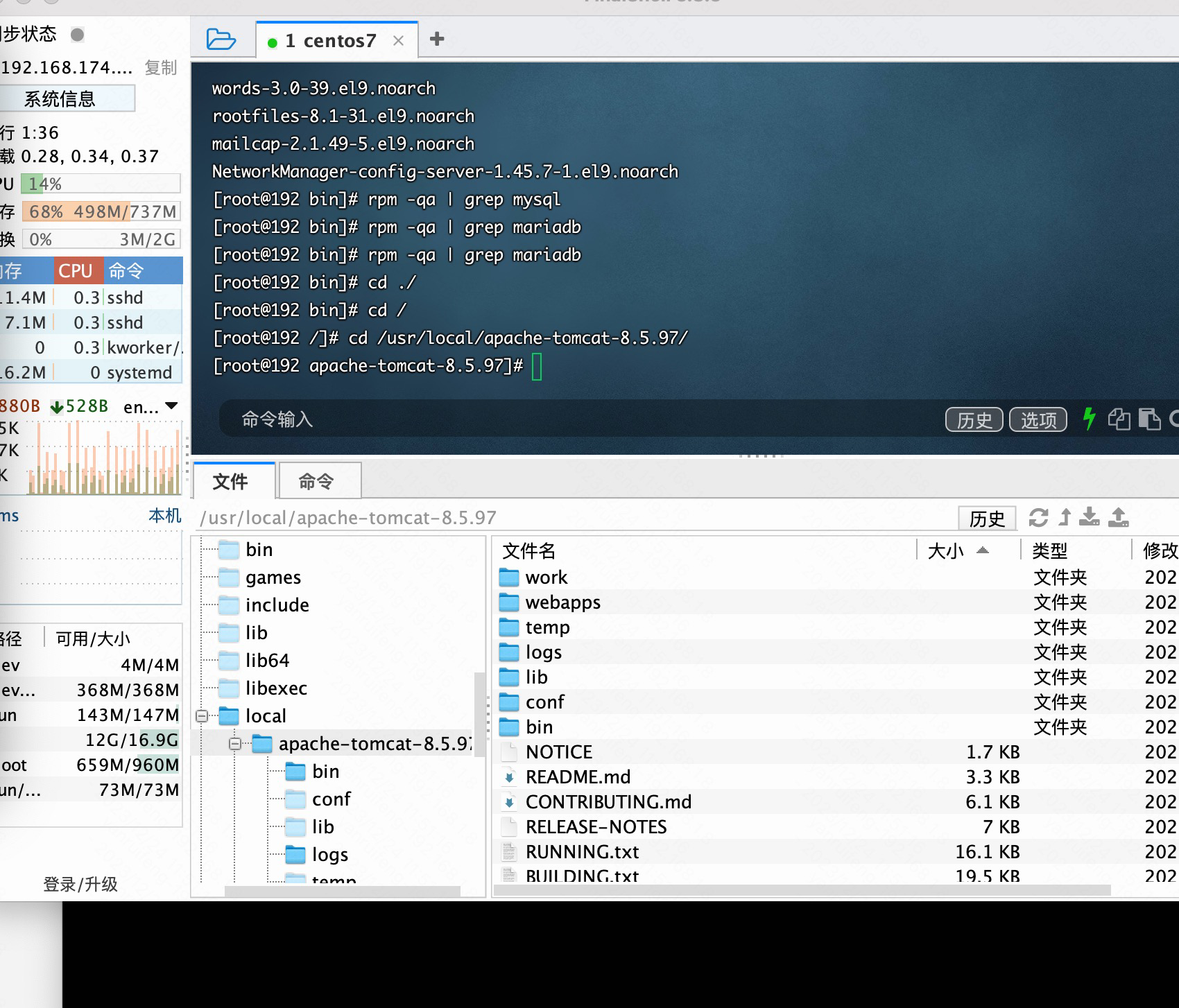
如果想启动tomcat 的话,进入bin目录 执行 ./startup.sh 服务就启动了。
然后启动完成后其实默认 你用ip访问 linux 上的tomcat服务器理论是不能访问的,因为linux服务器默认开启了防火墙,可以用防火墙命令进行操作,使它得以访问