本章来汇总一下leetcode中做过的背包问题,包括0-1背包和完全背包。
背包问题的通常形式为:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。求解将哪些物品装入背包里物品价值总和最大。0-1背包和完全背包的区别就在于物品能否重复拿取。
但是一般题目不会明确告诉你是背包问题,需要自己将问题进行转化。下面汇总一些常见的0-1背包和完全背包问题。
0-1背包问题
1、分割等和子集(★)

本题题意可以转化为:集合中能否出现总和为 sum / 2 的子集。 进而可以使用背包问题的思想来做:数组为背包,元素为物品。 又因为物品不可重复取,所以是0-1背包问题。
本题使用0-1背包动态规划算法思路如下:
- 先求出nums数组的元素总和sum, (sum/2) 即为背包的大小。
- 设dp数组,长度为sum/2 , 初始化为全0。dp[i]含义为:容量为i的背包最大能装多重的物品。
- 先遍历物品再遍历背包,并且为了防止物品重复放入,背包需要倒序遍历。
- 最后判断dp[target] 是否等于target,是则返回true。
java代码如下:
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int num : nums){
sum += num;
}
if(sum % 2 != 0) return false; //总和为奇数,不可能分割。
int target = sum / 2;
int[] dp = new int[target+1];
Arrays.fill(dp,0); //初始化dp数组为全0
//先遍历物品再遍历背包
for(int i=0; i<nums.length; i++){
for(int j=target; j>=nums[i]; j--){
dp[j] = Math.max(dp[j] , dp[j-nums[i]] + nums[i]);
}
}
if(dp[target] == target) return true;
return false;
}
}2、最后一块石头的重量II
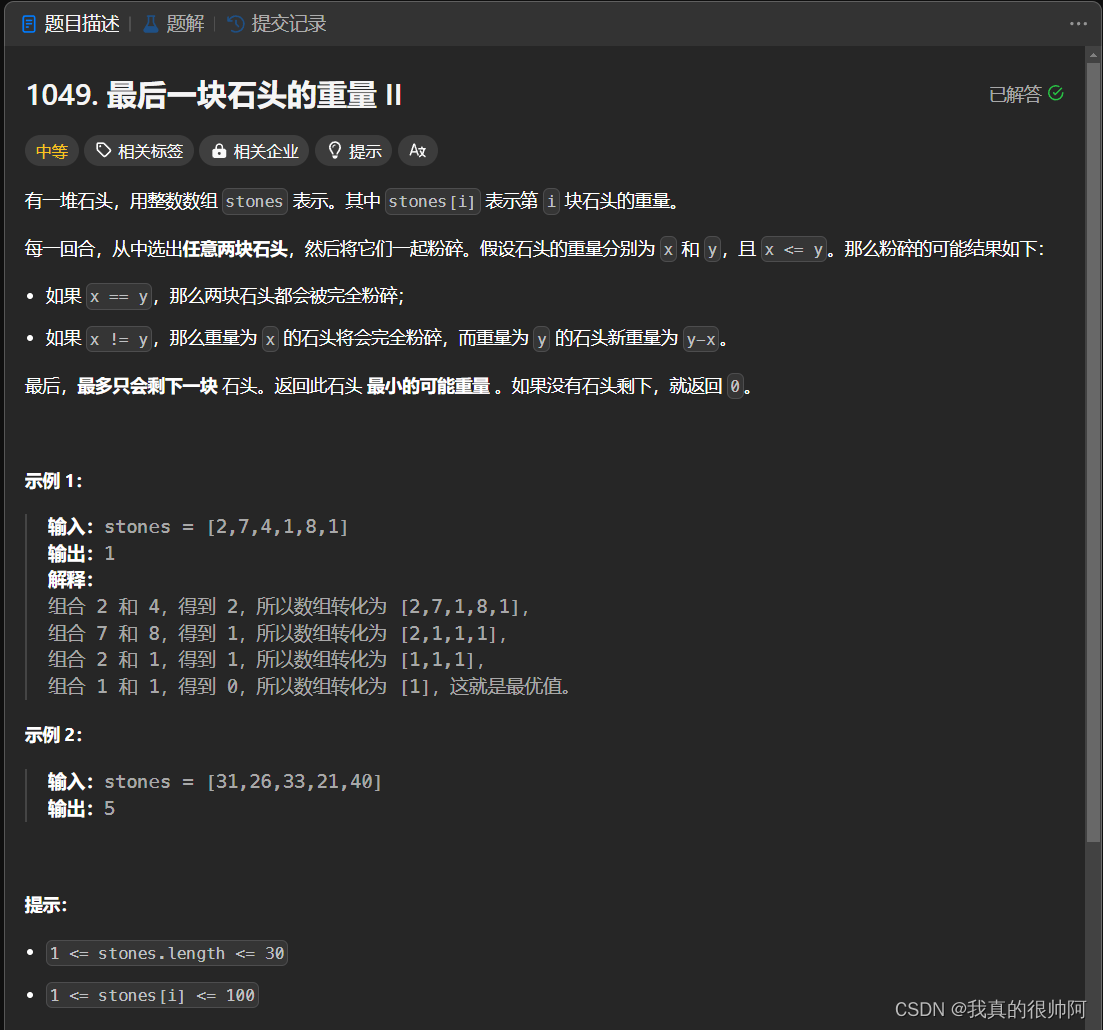
本题类似于上一题,可以转化为0-1背包问题。区别在于:本题如果可以分成等分量的两个子集,返回0;如果不能,则需要返回两子集的最小差值。
按照上一题的思路,java代码如下:
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for(int stone : stones){
sum += stone;
}
int target = sum / 2;
int[] dp = new int[target+1];
Arrays.fill(dp,0);
for(int i=0; i<stones.length; i++){
for(int j=target; j>=stones[i]; j--){
dp[j] = Math.max(dp[j] , dp[j-stones[i]]+stones[i]);
}
}
return sum-dp[target]*2;
}
}3、目标和(★)

本题难点在于如何将题意转化为0-1背包问题。 可以这么想:将nums数组分为两个子集:子集一全加正号,子集二全加负号,然后像上题一样,两子集相碰撞(相减),结果为target值。设sum为总元素和,positive_sum为正数和,那么(sum-positive_sum)就为负数和,有如下等式成立:positive_sum - (sum-positive_sum) = target , 解得positive_sum = (target + sum) / 2 。
此时成功将题意转化为0-1背包问题:positive_sum为背包大小,nums中元素为物品。 之前是要求背包所装物品的最大重量,而本题区别在于要求能装满背包的方法个数。整体思路不变,区别就在于递归公式要变化一下:
dp[j] = dp[j] + dp[j-nums[i]]
这个递推公式用于求解装满背包的最大方法个数,可以记一下。
那么设的dp数组含义就变为:dp[i]表示装满大小为 i 的背包的方法个数。
java代码如下:
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int num : nums){
sum += num;
}
if((target + sum) % 2 != 0) return 0; //没有办法得到运算结果target
int positive_sum = (target + sum) / 2; //正数和
if(positive_sum < 0) return 0;//正数和不为负数
int[] dp = new int[positive_sum+1];
dp[0] = 1;
for(int i=0; i<nums.length; i++){
for(int j=positive_sum; j>=nums[i]; j--){
dp[j] = dp[j] + dp[j-nums[i]];
}
}
return dp[positive_sum];
}
}完全背包问题
1、零钱兑换II
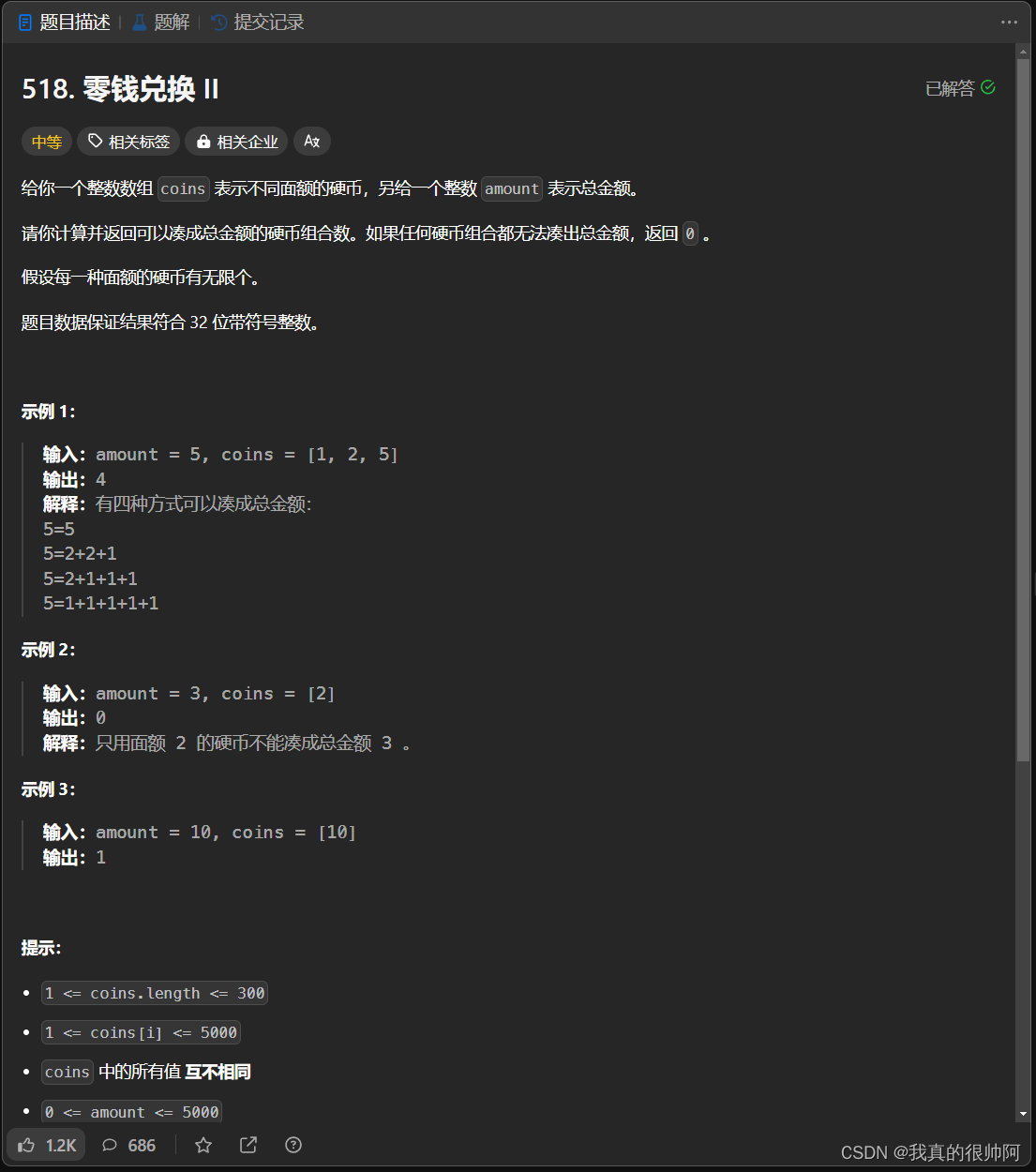
分析题意,有两个关键点:①求得是组合数,组合和排列不一样,组合没有顺序,而排列有。②硬币有无限个,因此本题为完全背包问题。 背包为总金额,物品为硬币,要求的是装满背包有多少种方法,和 上一题“目标和”要求的东西一样,因此递推公式为:
dp[j] = dp[j] + dp[j-nums[i]]
本题是完全背包问题,物品个数为无限,因此遍历的第二层循环不是倒序遍历了,而是正序。(当初倒序遍历就是为了防止重复拿取物品,完全背包可以重复拿取物品)。
遍历顺序也有讲究,先遍历物品再遍历背包求得是组合数,先遍历背包再遍历物品求得是排列数,此题要求组合数,因此先遍历物品再遍历背包。
java代码如下:
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] = 1;
for(int i=0; i<coins.length; i++){
for(int j=coins[i]; j<=amount; j++){
dp[j] = dp[j] + dp[j-coins[i]];
}
}
return dp[amount];
}
}2、组合总和IV

有了上述题的基础,本题可以说是手拿把掐了。
首先物品可以重复拿取,是完全背包问题。题目求的是排列数(虽然题目说的组合数,但根据示例来看其实是求排列数),因此遍历顺序应该是先遍历背包再遍历物品。 最后求的是装满背包的方法数,所以递推公式是:dp[j] = dp[j] + dp[j-nums[i]]。
java代码如下:
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
dp[0] = 1;
for(int i=0; i<=target; i++){
for(int j=0; j<nums.length; j++){
if(i >= nums[j]){
dp[i] = dp[i] + dp[i-nums[j]];
}
}
}
return dp[target];
}
}3、爬楼梯(★)
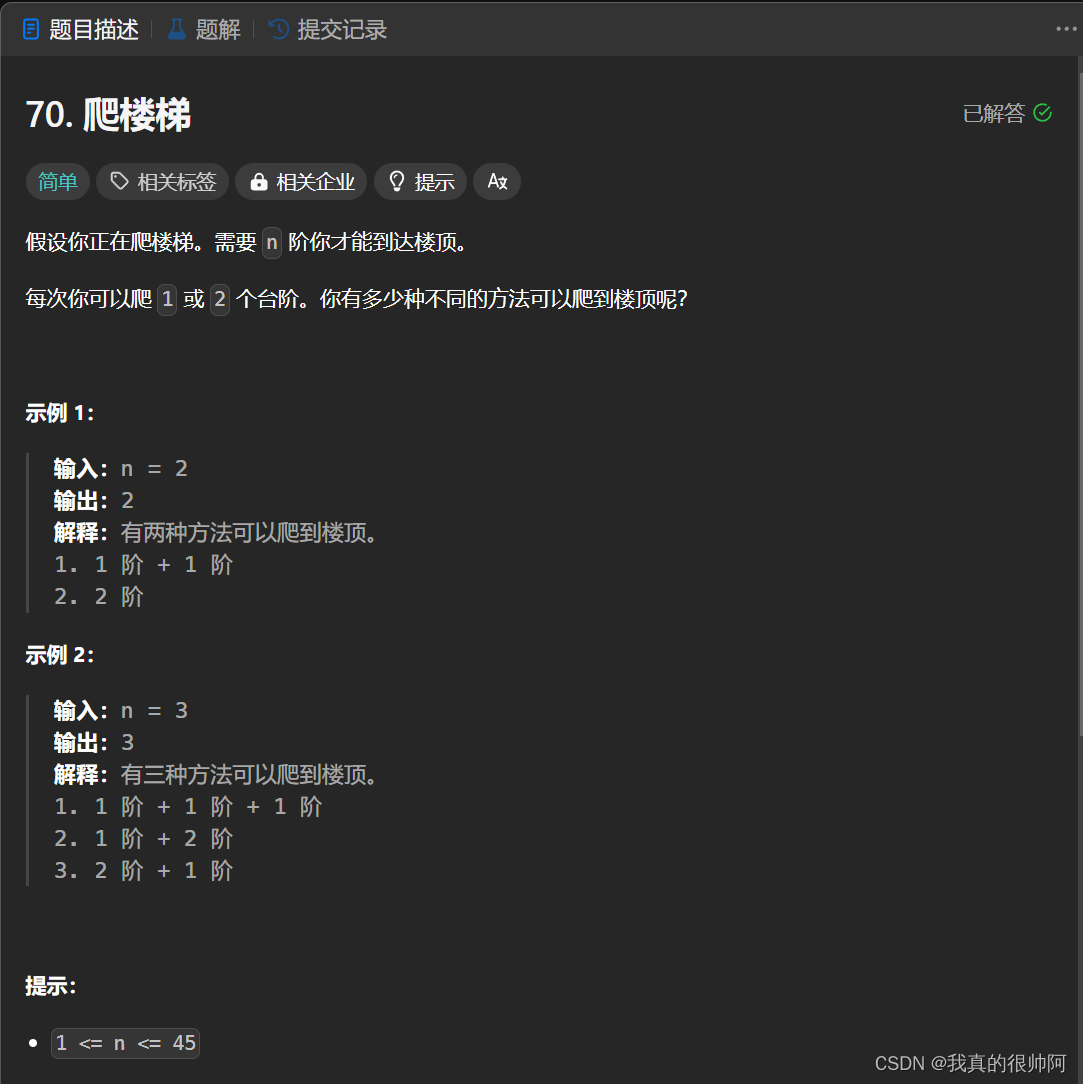
本题是动态规划系列梦开始的地方,一开始使用斐波那契数列做的,现在一看就是个完全背包问题,背包大小是总楼梯阶数n,物品是1或2。 要求装满背包的方法个数。
和上题可以说一毛一样,直接上代码:
class Solution {
public int climbStairs(int n) {
int dp[] = new int[n+1];
dp[0] = 1;
for(int i=0; i<=n; i++){
for(int j=1; j<=2; j++){
if(i >= j){
dp[i] = dp[i] + dp[i-j];
}
}
}
return dp[n];
}
}4、零钱兑换(★)
本题属于完全背包问题,由于题目求得是凑成总金额所需得最少硬币个数,所以求组合数和排列数都可以,都不影响最后得最少硬币个数,因此遍历顺序先物品或者先背包都是可以的。
本题由于求的是最少硬币个数,我们将dp[i]定义为:装满大小为 i 的背包所需最少物品个数。 递归公式为:
dp[j] = Math.min(dp[j] , dp[j-coins[i]]+1);
此外,初始化dp数组的时候除了dp[0] 初始化为0之外,其他都要初始化为最大值。
java代码如下:
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];//dp[j]:装满大小为j的背包所需的最少硬币个数
Arrays.fill(dp,Integer.MAX_VALUE);
dp[0] = 0;
for(int i=0; i<coins.length; i++){
for(int j=coins[i]; j<=amount; j++){
if(dp[j-coins[i]]!=Integer.MAX_VALUE){
dp[j] = Math.min(dp[j] , dp[j-coins[i]]+1);
}
}
}
return dp[amount] == Integer.MAX_VALUE? -1 : dp[amount];
}
}5、完全平方数(★)

本题和 “零钱兑换”非常相似,同属于完全背包,并且求的也是装满背包所需的最小物品数。
本题的背包为给定的整数n,物品为自然数的平方,如1的平方、2的平方......
思路同上一题,java代码如下:
class Solution {
public int numSquares(int n) {
//背包:整数n | 物品:完全平方数的平方
int[] dp = new int[n+1]; //dp[i]:装满大小为i的背包所需的最小物品数
Arrays.fill(dp,Integer.MAX_VALUE);
dp[0] = 0;
for(int i=1; i<=n; i++){
for(int j=i*i; j<=n; j++){
if(dp[j-i*i] != Integer.MAX_VALUE){
dp[j] = Math.min(dp[j] , dp[j-i*i]+1);
}
}
}
return dp[n];
}
}6、单词拆分(★)
本题由于单词可以重复使用,因此是完全背包问题。 背包为字符串s,物品为wordDict里的字符串。 要求使用物品能否装满背包。 因此设dp数组,dp[i]的含义为:大小为i的背包能否被物品装满。 由于物品(单词)之间有顺序之分,因此本题属于排列问题,先遍历背包再遍历物品。
直接看java代码:
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
int capacity = s.length();
int[] dp = new int[capacity+1]; //dp[i]:大小为i的背包能否被物品装满
dp[0] = 1;
for(int i=1; i<=capacity; i++){
for(String word : wordDict){
int len = word.length();
if(i>=len && dp[i-len]==1 && word.equals(s.substring(i-len,i))){
dp[i] = 1;
break;
}
}
}
return dp[capacity] == 1? true : false;
}
}总结
以上题目过关背包问题基本上就没问题了,最后总结一下背包问题的套路:
- 0-1背包问题遍历背包的时候需要倒序遍历,以防止重复拿取物品。完全背包可以重复拿取物品,因此是正序遍历。
- 题目求组合数和排列数的遍历顺序是不一样的:求组合数要先遍历物品再遍历背包,求排列数要先遍历背包再遍历物品。
- 递归公式根据题目要求不一样而不一样,下面列举常见的几个递推公式:
- 求尽可能装满背包的最大重量:dp[j] = Math.max(dp[j] , dp[j-nums[i]] + nums[i]); 如0-1背包的第1、2题。
- 求装满背包的方法种数:dp[j] = dp[j] + dp[j-nums[i]]; 如0-1背包的第3题、完全背包的第1题、第2题、第3题。
- 求装满背包的最小物品数:dp[j] = Math.min(dp[j] , dp[j-nums[i]]+1); 如完全背包的第4题、第5题。
- 单词拆分这题单独记一下吧。




![[MySQL binlog实战] 增量同步与数据搜索~从入门到精通](https://img-blog.csdnimg.cn/img_convert/aaf6b932169e50ac55f53acb28b55be0.png)