文章目录
- 2023/12/18
- LeetCode每日一刷:[20. 有效的括号](https://leetcode.cn/problems/valid-parentheses/)
- 2023/12/19
- LeetCode每日一刷:[150. 逆波兰表达式求值(后缀表达式运算)](https://leetcode.cn/problems/evaluate-reverse-polish-notation/)
- 联想思考:如何将中缀表达式转换为后缀表达式?
- LeetCode今日两刷: [232.双栈模拟队列](https://leetcode.cn/problems/implement-queue-using-stacks/description/)
- 2023/12/20
- LeetCode每日一刷:[225. 用队列实现栈](https://leetcode.cn/problems/implement-stack-using-queues/)
- 2023/12/21
- LeetCode每日一刷:[103. 二叉树的锯齿形层序遍历](https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/)
- 2023/12/22
- LeetCode每日一刷:[23. 合并 K 个升序链表](https://leetcode.cn/problems/merge-k-sorted-lists/)<同12/09>
- LeetCode每五日一总结【12/18--12/22】
- **2023/12/18**
- **2023/12/19**
- **2023/12/20**
- **2023/12/21**
- **2023/12/22**

2023/12/18
LeetCode每日一刷:20. 有效的括号
给定一个只包括
'(',')','{','}','[',']'的字符串s,判断字符串是否有效。有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()" 输出:true示例 2:
输入:s = "()[]{}" 输出:true示例 3:
输入:s = "(]" 输出:false提示:
1 <= s.length <= 104s仅由括号'()[]{}'组成
class Solution {
private static final Map<Character,Character> map = new HashMap<Character,Character>(){{
put('{','}'); put('[',']'); put('(',')'); put('?','?');
}};
public boolean isValid(String s) {
if(s.length() > 0 && !map.containsKey(s.charAt(0))) return false;
LinkedList<Character> stack = new LinkedList<Character>() {{ add('?'); }};
for(Character c : s.toCharArray()){
if(map.containsKey(c)) stack.addLast(c);
else if(map.get(stack.removeLast()) != c) return false;
}
return stack.size() == 1;
}
}
以上思路出自
作者:Krahets
链接:https://leetcode.cn/problems/valid-parentheses/
来源:LeetCode(LeetCode)
public boolean isValid(String s) {
// 创建一个栈
Stack<Character> stack = new Stack<>();
// 遍历字符串中的每一个字符
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
// 如果字符是左括号,则将右括号压入栈中
if (c == '(') {
stack.push(')');
} else if (c == '[') {
stack.push(']');
} else if (c == '{') {
stack.push('}');
} else {
// 如果字符是右括号,则判断栈中是否有对应的左括号
if (!stack.isEmpty() && c == stack.peek()) {
stack.pop();
} else {
// 如果没有对应的左括号,则返回false
return false;
}
}
}
// 如果栈为空,则返回true
return stack.isEmpty();
}
这是一个 Java 代码,定义了一个名为
isValid的方法,该方法接受一个字符串s作为输入,并返回一个布尔值,表示该字符串是否是一个有效的括号序列。该方法使用一个堆栈来跟踪在输入字符串中遇到的 opening parentheses(括号、大括号)。当它遇到一个 opening parenthesis 时,将与之对应的 closing parenthesis 压入堆栈。如果它遇到一个 closing parenthesis,它会检查它是否与堆栈的顶部元素匹配。如果它匹配,它会从堆栈中弹出顶部元素。如果不匹配,它会返回
false,表示输入字符串不是有效的括号序列。在处理完输入字符串中的所有字符后,该方法检查堆栈是否为空。如果为空,这意味着所有括号都已匹配,输入字符串是一个有效的括号序列。如果堆栈不为空,则表示存在未匹配的括号,输入字符串不是一个有效的括号序列。
以下是代码的逐行解释:
- 创建一个名为
stack的空堆栈。- 遍历输入字符串
s中的每个字符c。- 如果
c是 opening parenthesis((、[或{),将与之对应的 closing parenthesis 压入堆栈()或]或}, respectively)。- 如果
c是 closing parenthesis,检查它是否与堆栈的顶部元素匹配。
- 如果它匹配,从堆栈中弹出顶部元素。
- 如果它不匹配,返回
false,表示输入字符串不是有效的括号序列。- 如果
c既不是 opening parenthesis 也不是 closing parenthesis,检查它是否与堆栈的顶部元素匹配。
- 如果它匹配,从堆栈中弹出顶部元素。
- 如果它不匹配,返回
false,表示输入字符串不是有效的括号序列。- 在处理完输入字符串中的所有字符后,检查堆栈是否为空。
- 如果为空,返回
true,表示输入字符串是一个有效的括号序列。- 如果不为空,返回
false,表示输入字符串不是一个有效的括号序列。
2023/12/19
LeetCode每日一刷:150. 逆波兰表达式求值(后缀表达式运算)
给你一个字符串数组
tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22提示:
1 <= tokens.length <= 104tokens[i]是一个算符("+"、"-"、"*"或"/"),或是在范围[-200, 200]内的一个整数逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。- 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。- 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
//jdk新语法,不需要写break
public int evalRPN(String[] tokens) {
//定义一个栈数据结构
LinkedList<Integer> stack = new LinkedList<>();
//迭代字符串数组中的每一个元素
for (String s : tokens) {
switch (s) {
//如果当前字符为" + ",则将栈顶两个元素弹出,做和运算后再压入栈中
case "+" -> {
int b = stack.pop();
int a = stack.pop();
stack.push(a + b);
}
//如果当前字符串为" - ",则将栈顶两个元素弹出,做差运算后再压入栈中(注意弹栈顺序:先弹栈的做减数)
case "-" -> {
int b = stack.pop();
int a = stack.pop();
stack.push(a - b);
}
//如果当前字符串为" * ",则将栈顶两个元素弹出,做乘积运算后再压入栈中
case "*" -> {
int b = stack.pop();
int a = stack.pop();
stack.push(a * b);
}
//如果当前字符串为" / ",则将栈顶两个元素弹出,做除法运算后再压入栈中(注意弹栈顺序:先弹栈的做除数)
case "/" -> {
int b = stack.pop();
int a = stack.pop();
stack.push(a / b);
}
//如果当前字符串为非运算符,则转为int类型后,压入栈中
default -> {
stack.push(Integer.parseInt(s));
}
}
}
//最后将栈中最后一个也是唯一一个元素返回,即是后缀表达式运算结果
return stack.pop();
}
//jdk旧语法
LinkedList<Integer> stack = new LinkedList<>();
for (String s : tokens) {
switch (s) {
case "+": {
int b = stack.pop();
int a = stack.pop();
stack.push(a + b);
break;
}
case "-": {
int b = stack.pop();
int a = stack.pop();
stack.push(a - b);
break;
}
case "*": {
int b = stack.pop();
int a = stack.pop();
stack.push(a * b);
break;
}
case "/": {
int b = stack.pop();
int a = stack.pop();
stack.push(a / b);
break;
}
default: {
stack.push(Integer.parseInt(s));
}
}
}
return stack.pop();
}
联想思考:如何将中缀表达式转换为后缀表达式?
思路: 1. 遇到非运算符 直接拼串 2. 遇到 + - * / - 它的优先级比栈顶运算符高, 入栈, 如: 栈中是 + 当前是 * - 否则把栈里优先级 >= 它 的都出栈, 它再入栈, 如: 栈中是 +*, 当前是 - 3. 遍历完成, 栈里剩余运算符依次出栈 4. 如果带() - 左括号直接入栈, 左括号优先设置为0 - 右括号就把栈里到左括号为止的所有运算符出栈 | | | | | | _____ a+b ab+ a+b-c ab+c- a*b+c ab*c+ a+b*c abc*+ a+b*c-d abc*+d- (a+b)*c ab+c* (a+b*c-d)*e abc*+d-e* a*(b+c) abc+*
//计算优先级
static int priority(char c) {
return switch (c) {
case '+', '-' -> 1; // + - 优先级为 1
case '*', '/' -> 2; // * / 优先级为 2
case '(' -> 0;
default -> throw new IllegalArgumentException("输入的参数不合法 " + c);
};
}
static String infixToSuffix(String exp) {
//定义一个StringBuilder字符串变量,用于拼接结果集字符串
StringBuilder result = new StringBuilder(exp.length());
//定义一个栈,用于存放按照规定的优先级规律存放 运算符
LinkedList<Character> stack = new LinkedList<>();
//遍历字符串参数(中缀表达式)
for (int i = 0; i < exp.length(); i++) {
//取到表达式中的每一个字符
char c = exp.charAt(i);
//如果取到的字符为运算符或者括号,则根据规则入栈或者出栈,如果取到的字符是非运算符和括号,则直接参与字符串拼接
switch (c) {
case '+', '-', '*', '/' -> {
//如果栈是空的,则直接将字符串压入栈中
if (stack.isEmpty()) {
stack.push(c);
} else {
//如果栈非空,则判断当前运算符的优先级及栈顶运算符优先级,如果当前运算符优先级高于栈顶运算符优先级,则将当前运算符压人栈
if (priority(c) > priority(stack.peek())) {
stack.push(c);
} else {//如果当前运算符优先级小于或等于栈顶运算符优先级,则将栈顶运算符弹栈后拼接到结果集字符串中,并循环比较,如果栈被弹空,停止循环
while (!stack.isEmpty() && priority(c) <= priority(stack.peek())) {
result.append(stack.pop());
}
//最后将当前运算符压入栈中
stack.push(c);
}
}
}//如果当前字符为左括号,则直接压入栈中
case '(' -> {
stack.push('(');
}//如果当前运算符是右括号,则将栈中左括号上面的所有运算符弹栈后拼接到结果集字符串中
case ')' -> {
while (!stack.isEmpty()&& stack.peek()!='('){
result.append(stack.pop());
}
//最后将左括号从栈中弹出
stack.pop();
}
//字符为非运算符,直接拼接到结果集字符串中
default -> result.append(c);
}
}
//当字符串中每个字符都被迭代后,将栈中还未弹栈的运算符弹出并拼接到结果集字符串中
while (!stack.isEmpty()){
result.append(stack.pop());
}
//返回StringBuilder的toString字符串类型
return result.toString();
}
LeetCode今日两刷: 232.双栈模拟队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(
push、pop、peek、empty):实现
MyQueue类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。- 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty- 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)进阶:
- 你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。
给LeetCode题目用的自实现栈,可以定义为静态内部类
class ArrayStack<E> {
private E[] array;
private int top; // 栈顶指针
@SuppressWarnings("all")
public ArrayStack(int capacity) {
this.array = (E[]) new Object[capacity];
}
public boolean push(E value) {
if (isFull()) {
return false;
}
array[top++] = value;
return true;
}
public E pop() {
if (isEmpty()) {
return null;
}
return array[--top];
}
public E peek() {
if (isEmpty()) {
return null;
}
return array[top - 1];
}
public boolean isEmpty() {
return top == 0;
}
public boolean isFull() {
return top == array.length;
}
}
参考解答,注意:题目已说明
- 调用 push、pop 等方法的次数最多 100
public class E04Leetcode232 {
/*
队列头 队列尾
s1 s2
顶 底 底 顶
abc
push(a)
push(b)
push(c)
pop()
*/
ArrayStack<Integer> s1 = new ArrayStack<>(100);
ArrayStack<Integer> s2 = new ArrayStack<>(100);
public void push(int x) {
s2.push(x);
}
public int pop() {
if (s1.isEmpty()) {
while (!s2.isEmpty()) {
s1.push(s2.pop());
}
}
return s1.pop();
}
public int peek() {
if (s1.isEmpty()) {
while (!s2.isEmpty()) {
s1.push(s2.pop());
}
}
return s1.peek();
}
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
}
提交版代码:
class MyQueue
ArrayStack<Integer> s1 = new ArrayStack<>(100);
ArrayStack<Integer> s2 = new ArrayStack<>(100);
public void push(int x) {
s1.push(x);
}
public int pop() {
if (s2.isEmpty()) {
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
}
return s2.pop();
}
public int peek() {
if (s2.isEmpty()) {
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
}
return s2.peek();
}
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
static class ArrayStack<E>{
private final E[] stack;
private int top;
@SuppressWarnings("ALL")
public ArrayStack(int capacity) {
stack = (E[]) new Object[capacity];
}
public boolean push(E value) {
if (isFull()) {
return false;
}
stack[top++] = value;
return true;
}
public E pop() {
if(isEmpty()){
return null;
}
return stack[--top];
}
public E peek() {
if(isEmpty()){
return null;
}
return stack[top-1];
}
public boolean isEmpty() {
return top == 0;
}
public boolean isFull() {
return top == stack.length;
}
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/
LeetCode官方题解:
class MyQueue {
Deque<Integer> inStack;
Deque<Integer> outStack;
public MyQueue() {
inStack = new ArrayDeque<Integer>();
outStack = new ArrayDeque<Integer>();
}
public void push(int x) {
inStack.push(x);
}
public int pop() {
if (outStack.isEmpty()) {
in2out();
}
return outStack.pop();
}
public int peek() {
if (outStack.isEmpty()) {
in2out();
}
return outStack.peek();
}
public boolean empty() {
return inStack.isEmpty() && outStack.isEmpty();
}
//将输入栈中的元素弹栈并压入输出栈
private void in2out() {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
}
作者:LeetCode官方题解
链接:https://leetcode.cn/problems/implement-queue-using-stacks/
来源:LeetCode(LeetCode)
思路
将一个栈当作输入栈,用于压入 push 传入的数据;另一个栈当作输出栈,用于 pop 和 peek 操作。
每次 pop 或 peek 时,若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。
2023/12/20
LeetCode每日一刷:225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(
push、top、pop和empty)。实现
MyStack类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。- 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false] 解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty- 每次调用
pop和top都保证栈不为空**进阶:**你能否仅用一个队列来实现栈。
提交代码:
class MyStack {
ArrayQueue5<Integer> queue = new ArrayQueue5<>(100);
private int size = 0;
public void push(int x) {
queue.offer(x);
for(int i =0;i<size;i++){
queue.offer(queue.poll());
}
size++;
}
public int pop() {
size--;
return queue.poll();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
static class ArrayQueue5<E>{
private final E[] array;
int head = 0;
int tail = 0;
@SuppressWarnings("all")
public ArrayQueue5(int capacity) {
/*//抛异常
if ((capacity & capacity - 1) != 0) {
throw new IllegalArgumentException("请传入容量为2的N次方的容量参数");
}*/
//增大容量为大于当前参数的最小2的n次方 13 -> 16 22 -> 32
if ((capacity & capacity - 1) != 0) {
int n = (int) ((Math.log10(capacity) / Math.log10(2)) + 1);//计算大于参数的最小2的n次方的n
capacity = 1 << n; //左移运算符,相当于乘2 , 1 << n相当于 2^n
System.out.println(capacity);
}
array = (E[]) new Object[capacity];
}
public boolean offer(E value) {
if (isFull()) {
return false;
}
//使用位运算,规律:当一个数对2的整数次的数取模时,余数=这个数 &(按位与) 2的整数次-1
// 666 % 8 = 666 & 7
/*
求模运算:
- 如果除数是 2 的 n 次方
- 那么被除数的后 n 位即为余数 (模)
- 求被除数的后 n 位方法: 与 2^n-1 按位 与
*/
array[tail & array.length - 1] = value;
tail++;
return true;
}
public E poll() {
if (isEmpty()) {
return null;
}
E value = array[head & array.length - 1];
head++;
return value;
}
public E peek() {
if (isEmpty()) {
return null;
}
E value = array[head & array.length - 1];
return value;
}
public boolean isEmpty() {
return tail == head;
}
public boolean isFull() {
return (tail - head) == array.length;
}
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
官方题解:
class MyStack {
Queue<Integer> queue;
/** Initialize your data structure here. */
public MyStack() {
queue = new LinkedList<Integer>();
}
/** Push element x onto stack. */
public void push(int x) {
int n = queue.size();
queue.offer(x);
for (int i = 0; i < n; i++) {
queue.offer(queue.poll());
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.poll();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
一个队列
方法一使用了两个队列实现栈的操作,也可以使用一个队列实现栈的操作。使用一个队列时,为了满足栈的特性,即最后入栈的元素最先出栈,同样需要满足队列前端的元素是最后入栈的元素。
入栈操作时,首先获得入栈前的元素个数 n,然后将元素入队到队列,再将队列中的前 n 个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端的元素即为新入栈的元素,且队列的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保队列的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可,获得栈顶元素操作只需要获得队列的前端元素并返回即可(不移除元素)。
由于队列用于存储栈内的元素,判断栈是否为空时,只需要判断队列是否为空即可。
2023/12/21
LeetCode每日一刷:103. 二叉树的锯齿形层序遍历
给你二叉树的根节点
root,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。示例 1:
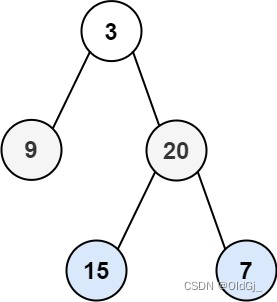
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[20,9],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目在范围
[0, 2000]内-100 <= Node.val <= 100
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
//定义一个存放结果集的链表
List<List<Integer>> result = new ArrayList<>();
//如果根节点为空,则直接返回空结果集
if (root == null) {
return result;
}
//定义一个队列
Queue<TreeNode> queue = new LinkedList<>();
//将根节点放入队列
queue.offer(root);
//记录每层节点个数
int c = 1;
//记录层数,以便对不同层做不同操作
boolean odd = true;//默认为奇数层
//如果队列非空
while (!queue.isEmpty()) {
//定义一个变量记录下一层节点个数
int n = 0;
//定义一个双端队列,用来存放每一层的节点
Deque<Integer> lever = new LinkedList<>();
//遍历当前层的每一个节点
for (int i = 0; i < c; i++) {
//将节点从队列中弹出
TreeNode treeNode = queue.poll();
if(odd){//如果为奇数层,则从尾部添加,正序
lever.offerLast(treeNode.val);
}else {//如果是偶数层,则从头部添加,逆序
lever.offerFirst(treeNode.val);
}
//如果节点有左孩子,则加入队列
if (treeNode.left != null) {
queue.offer(treeNode.left);
n++;
}
//如果节点有右孩子,则加入队列
if (treeNode.right != null) {
queue.offer(treeNode.right);
n++;
}
}
//将下一层节点数赋值给c
c = n;
//将每一层的节点组成的双端队列转换为链表加入到结果集
result.add(new LinkedList<>(lever));
//层数取反,奇数层变偶数层 偶数层变奇数层
odd=!odd;
}
return result;
}
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
这段Java代码定义了一个名为
zigzagLevelOrder的方法,该方法接受一个TreeNode类型的参数root,并返回一个List<List<Integer>>类型的结果。该方法的作用是按照zigzag顺序(即先从左到右,再从右到左)遍历二叉树的每一层,并将每一层的节点值存储在一个List<Integer>类型的列表中。以下是代码的详细解释:
- 定义一个存放结果集的链表
result,以及一个存放节点的队列queue。- 如果根节点为空,则直接返回空结果集。
- 定义一个变量
c来记录每层节点的个数,以及一个布尔变量odd来记录当前是奇数层还是偶数层。- 定义一个双端队列
lever来存放每一层的节点。- 遍历当前层的每一个节点,将节点从队列中弹出,并将其值添加到
lever队列中。如果是奇数层,则从队列尾部添加,即正序;如果是偶数层,则从队列头部添加,即逆序。- 如果当前节点的左孩子不为空,则将其加入队列
queue中。如果当前节点的右孩子不为空,则将其加入队列queue中。- 计算下一层节点的个数
n,并将队列queue中的节点个数赋值给c。- 将
lever队列中的节点值组成一个List<Integer>类型的列表,并将其添加到结果集result中。- 更新
odd变量,使其在奇数层和偶数层之间切换。- 循环执行步骤5到步骤9,直到队列为空。
- 返回结果集
result。此外,代码中还定义了一个名为
TreeNode的类,用于表示二叉树的节点。该类包含一个整数值val,以及两个指向子节点的引用left和right。

2023/12/22
LeetCode每日一刷:23. 合并 K 个升序链表<同12/09>
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6示例 2:
输入:lists = [] 输出:[]示例 3:
输入:lists = [[]] 输出:[]提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
/**
* 小顶堆
*/
public class MinHeap {
ListNode[] array;
int size;
public MinHeap(int capacity) {
array = new ListNode[capacity];
}
public boolean offer(ListNode value) {
if (isFull()) {
return false;
}
int child = size++;
int father = (child - 1) / 2;
while (child > 0 && value.val < array[father].val) {
array[child] = array[father];
child = father;
father = (child - 1) / 2;
}
array[child] = value;
return true;
}
public ListNode poll() {
if (isEmpty()) {
return null;
}
//1.交换堆顶元素与最后一个元素,删除最后一个元素
swap(0, size - 1);
size--;
ListNode e = array[size];
array[size] = null;// help GC
//2.将推顶元素与其孩子不断比较,到他合适位置
down(0);
return e;
}
private void down(int father) {
int left = father * 2 + 1;
int right = left + 1;
int min = father;// 假设父元素最小
if (left < size && array[left].val < array[min].val) {
min = left;
}
if (right < size && array[right].val < array[min].val) {
min = right;
}
if (min != father) {// 说明发生了交换,则有孩子比父亲大
swap(min, father);
down(min);
}
}
private void swap(int i, int j) {
ListNode t = array[j];
array[j] = array[i];
array[i] = t;
}
public boolean isEmpty() {
return size == 0;
}
public boolean isFull() {
return size == array.length;
}
}
//使用小顶堆解决
public ListNode mergeKLists(ListNode[] lists) {
/* p1
* 1 5 9 7 null
* p2
* 5 6 8 9 null
* p3
* 3 5 7 8 null
*
小顶堆: 1 5 3
空链表 null->
*/
MinHeap minHeap = new MinHeap(lists.length);
for (ListNode h : lists) {
if (h != null) {
minHeap.offer(h);
}
}
//新链表的哨兵节点
ListNode s = new ListNode(-1, null);
ListNode p = s;
while (!minHeap.isEmpty()) {
ListNode min = minHeap.poll();
p.next = min;
p = min;
if(min.next!=null){
minHeap.offer(min.next);//将链表的下一个节点加入小顶堆
}
}
return s;
}
使用小顶堆数据结构,先将链表中的头节点都加入小顶堆中,实例化一个新的链表【直接实例化一个新链表的哨兵节点即可】,定义一个指针,用来操作新链表,如果小顶堆不为空,则将小顶堆中poll出来的元素加入到新链表中,指针指向新的节点且将poll出来的节点的下一个节点再次加入到小顶堆(前提:下一节点存在),循环操作,直到小顶堆为空,说明已将全部节点转移到新链表,返回哨兵节点的next即可!
LeetCode每五日一总结【12/18–12/22】
2023/12/18
- 20.有效的括号
定义一个名为
isValid的方法,该方法接受一个字符串s作为输入,并返回一个布尔值,表示该字符串是否是一个有效的括号序列。 该方法使用一个堆栈来跟踪在输入字符串中遇到的 opening parentheses(括号、大括号)。当它遇到一个 opening parenthesis 时,将与之对应的 closing parenthesis 压入堆栈。如果它遇到一个 closing parenthesis,它会检查它是否与堆栈的顶部元素匹配。如果它匹配,它会从堆栈中弹出顶部元素。如果不匹配,它会返回
false,表示输入字符串不是有效的括号序列。 在处理完输入字符串中的所有字符后,该方法检查堆栈是否为空。如果为空,这意味着所有括号都已匹配,输入字符串是一个有效的括号序列。如果堆栈不为空,则表示存在未匹配的括号,输入字符串不是一个有效的括号序列。
2023/12/19
- 150.逆波兰表达式求值(后缀表达式运算)
使用**栈**数据结构,遍历逆波兰表达式数组,将**非运算符字符**压入栈中,如果遍历到的元素为运算符,则将**栈中弹出两个元素进行运算操作**,最后**将运算结果再次压入栈中**,直到遍历完整个字符串,将栈中最后一个元素弹出并返回即可!
- 联想思考:如何将中缀表达式转换为后缀表达式?
思路:1. 遇到非运算符 直接拼串 2. 遇到 + - * / - 它的优先级比栈顶运算符高, 入栈, 如: 栈中是 + 当前是 * - 否则把栈里优先级 >= 它 的都出栈, 它再入栈, 如: 栈中是 +*, 当前是 - 3. 遍历完成, 栈里剩余运算符依次出栈 4. 如果带() - 左括号直接入栈, 左括号优先设置为0 - 右括号就把栈里到左括号为止的所有运算符出栈 | | | | | | _____ a+b ab+ a+b-c ab+c- a*b+c ab*c+ a+b*c abc*+ a+b*c-d abc*+d- (a+b)*c ab+c* (a+b*c-d)*e abc*+d-e* a*(b+c) abc+*
- 232.双栈模拟队列
思路: 将一个栈当作输入栈,用于压入 push 传入的数据;另一个栈当作输出栈,用于 pop 和 peek 操作。 每次 pop 或 peek 时,若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。2023/12/20
- 225.用队列实现栈
思路:
使用一个队列
使用一个队列时,为了满足栈的特性,即最后入栈的元素最先出栈,同样需要满足队列前端的元素是最后入栈的元素。
入栈操作时,首先获得入栈前的元素个数 n,然后将元素入队到队列,再将队列中的前 n 个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端的元素即为新入栈的元素,且队列的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保队列的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可,获得栈顶元素操作只需要获得队列的前端元素并返回即可(不移除元素)。
由于队列用于存储栈内的元素,判断栈是否为空时,只需要判断队列是否为空即可。
2023/12/21
- 103.二叉树的锯齿形层序遍历
思路: 使用**队列**数据结构,先将二叉树的根节点入队,并定义一个变量记录二叉树每一层的节点个数,用于遍历每一层的节点,再定义一个双端队列,每次从队列出队的节点,根据层数的奇偶不同,选择从双端队列头部添加或者尾部添加,以此实现锯齿形层序遍历,判断如果从队列出队的节点存在左右孩子,则将其左右孩子入队列,循环此操作,直到队列为空。2023/12/22
- 23.合并 K 个升序链表<小顶堆实现>
使用小顶堆数据结构,先将链表中的头节点全都加入小顶堆中,实例化一个新的链表【直接实例化一个新链表的哨兵节点即可】,定义一个指针,用来操作新链表,如果小顶堆不为空,则将小顶堆中poll出来的元素加入到新链表中,指针指向新的节点且将poll出来的节点的下一个节点再次加入到小顶堆(前提:下一节点存在),循环操作,直到小顶堆为空,说明已将全部节点转移到新链表,返回哨兵节点的next即可!