本系列根据国外一个图形小哥的讲解为本，整合互联网的一些资料，结合自己的一些理解。

CPU vs GPU

CPU支持：

• 快速缓存
• 分支适应性
• 高性能

GPU支持：

• 多个 ALU
• 快速板载内存
• 并行任务的高吞吐量（在每个片段、顶点上执行着色器程序）

CPU 是更复杂的计算单元，因为它具有大量指令来支持各种功能。而GPU以SIMD方式工作（单指令多数据），它擅长使用数千个核心以并行方式处理大量数据。综上所述，CPU 非常适合任务并行性，GPU 非常适合数据并行。

渲染管线比较

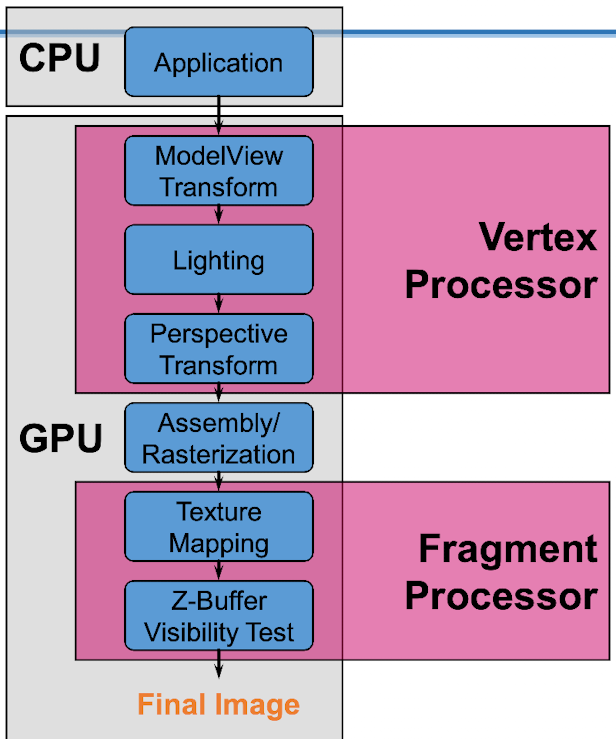
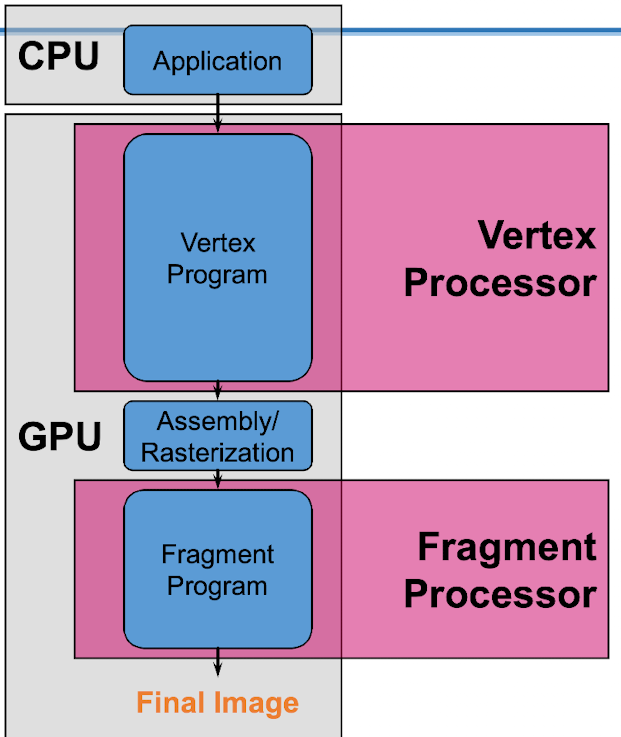
左侧的固定管线提供了固定的渲染管道，光栅化后有固定的方式处理顶点和片段。而可编程管道使我们能够灵活地控制顶点和片段处理器。

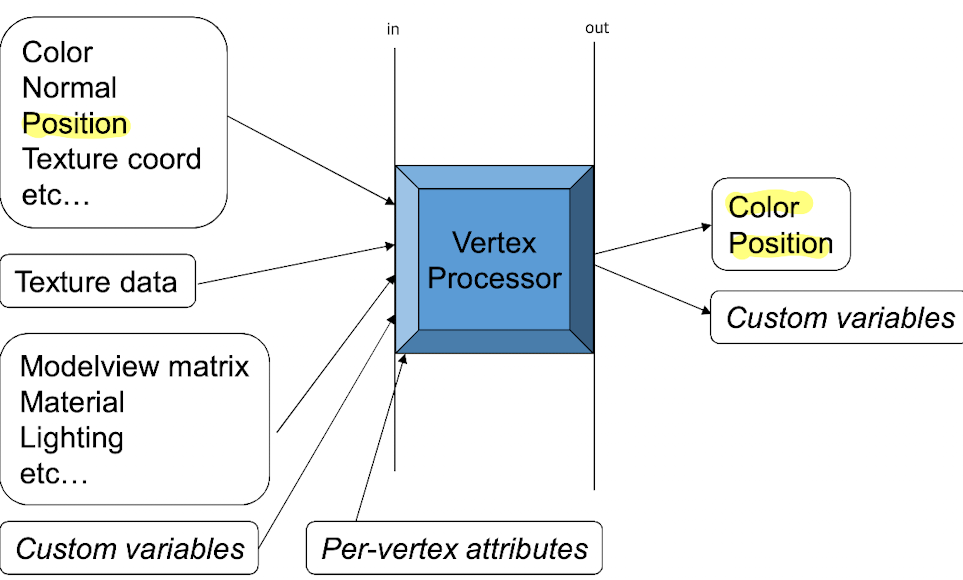
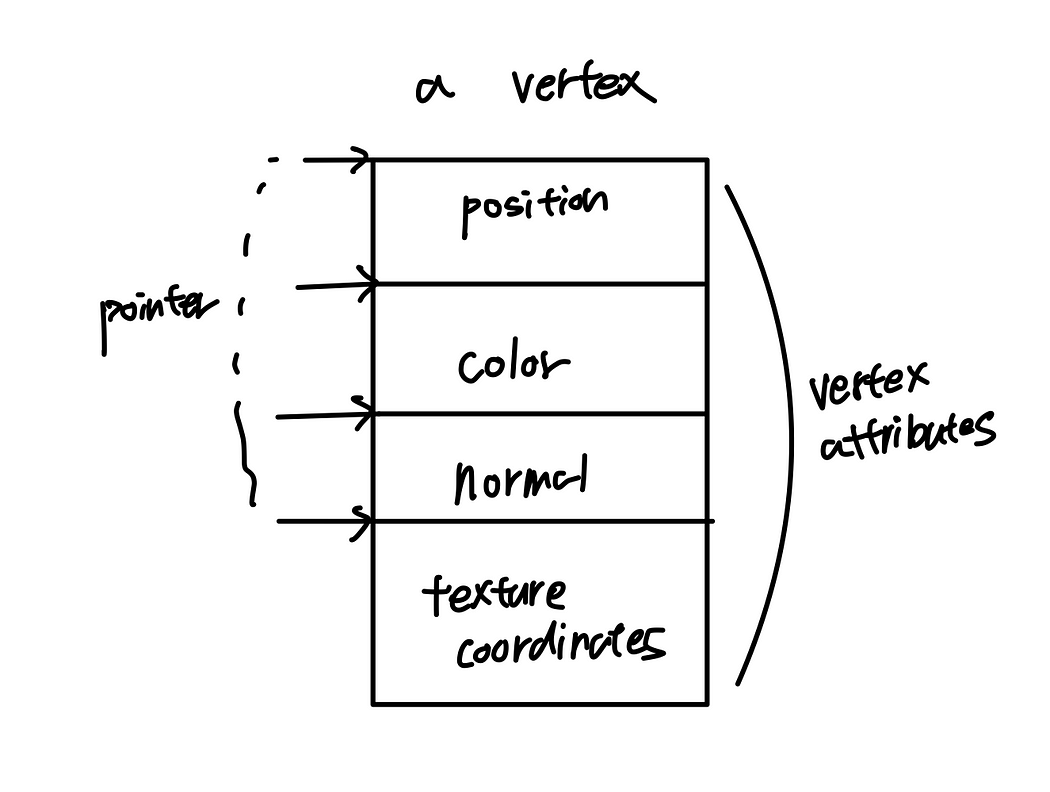
顶点处理器的输入/输出

作为输入数据，每个顶点中存储有颜色、法线、位置、纹理坐标和其他数据。

纹理数据是着色器变量，通常尺寸较大且速度较慢。

模型视图矩阵、材质和光照都是uniform变量，这些由所有顶点共享。

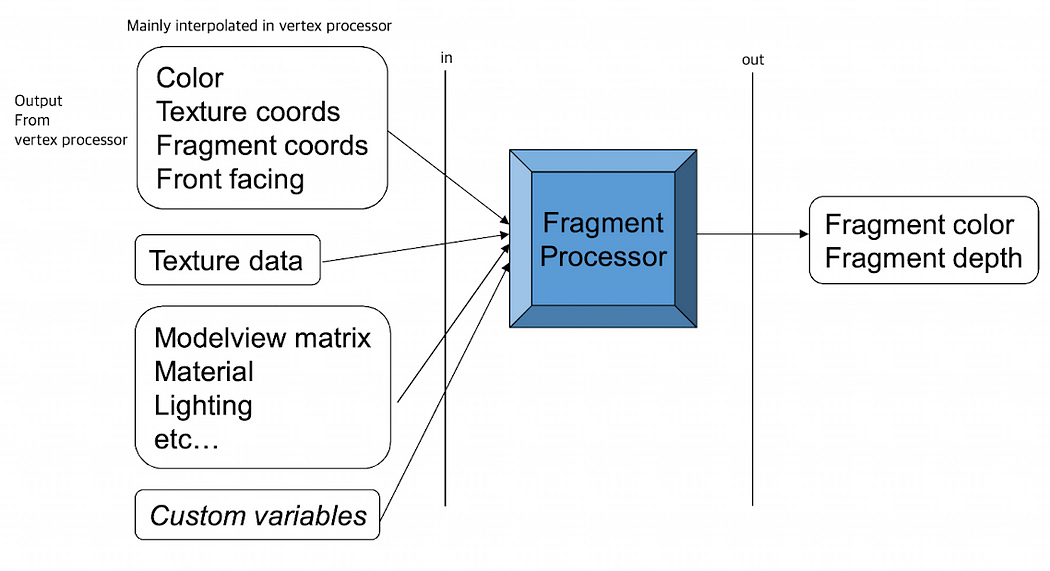
片段处理器的输入/输出

大多数输入数据来自顶点处理器。

例如，当我们想要使用 Gouraud 着色渲染场景时，我们应该在顶点着色器中为每个片段插入颜色因子。然后，在片段着色器中，我们只需将计算出的颜色分配给每个片段。

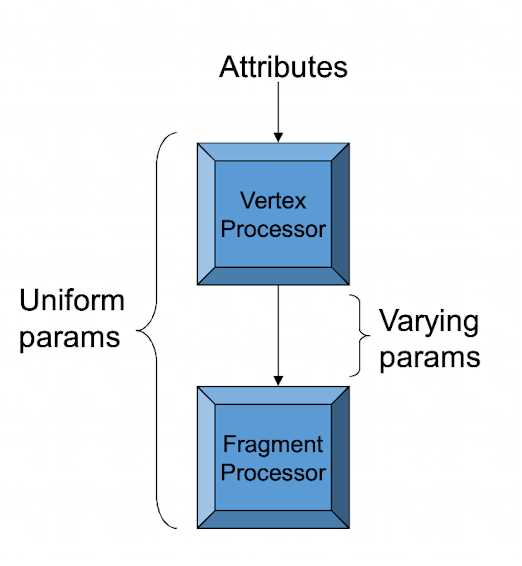
着色器如何通信？

• uniform参数：在整个执行过程中设置。
• attribute参数：为每个顶点设置。
• varying参数：从顶点着色器传递到片段着色器（例如逆转换法线）。对于不同的参数，两个处理器中使用相同的变量名称。

如何编写着色器

在现代openGL中，我们应该在着色器程序中编写光照处理逻辑。与简单着色方法相关，有两种着色方式：

• 逐顶点着色（gouraud 着色）

通过这种方式，我们计算顶点着色器内部的照明，然后将varying参数传递给片段着色器。

• 逐片段着色（phong 着色）

在片段着色中，对每个顶点的法线进行插值，然后通过将发现作为varying参数在片段着色器中计算照明。

归一化

照明计算可以使用法线向量和光方向向量的点积来计算。

我们可以采用单位向量来简化计算，因为两个向量归一化后点积的结果等于余弦项。

由于经过各种变换，向量的长度并不总是相同。所以在这种情况下我们需要不断地对向量进行归一化。

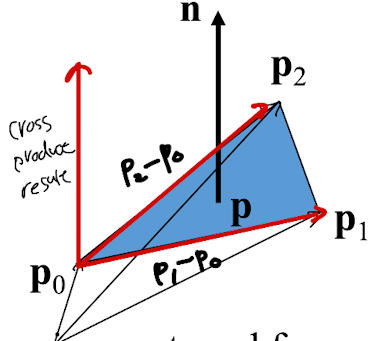
在右侧图像中，解释了如何获取三角形的法向量。

假设我们知道组成三角形的三个点，我们可以通过点相减得到三角形边的两个向量。然后，如果我们对顺时针方向的两个边向量进行叉积，我们可以得到一个与三角形表面正交的向量。经过归一化，最终我们得到了三角形的法向量。

2. 指定光源（静态）

对于每个光源，我们可以设置一个RGBA。

vec4 diffuse0 = vec4(1.0, 0.0, 0.0, 1.0);
vec4 ambient0 = vec4(1.0, 0.0, 0.0, 1.0);
vec4 specular0= vec4(1.0, 0.0, 0.0, 1.0);
vec4 light_pos = vec4(1.0, 2.0, 3.0, 1.0);

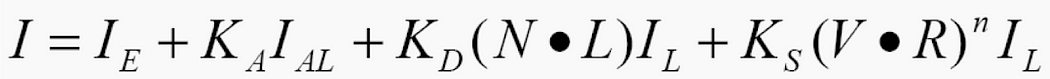
局部 BRDF 照明模型遵循此方程。

根据光源的类型，我们需要不同地计算照度。

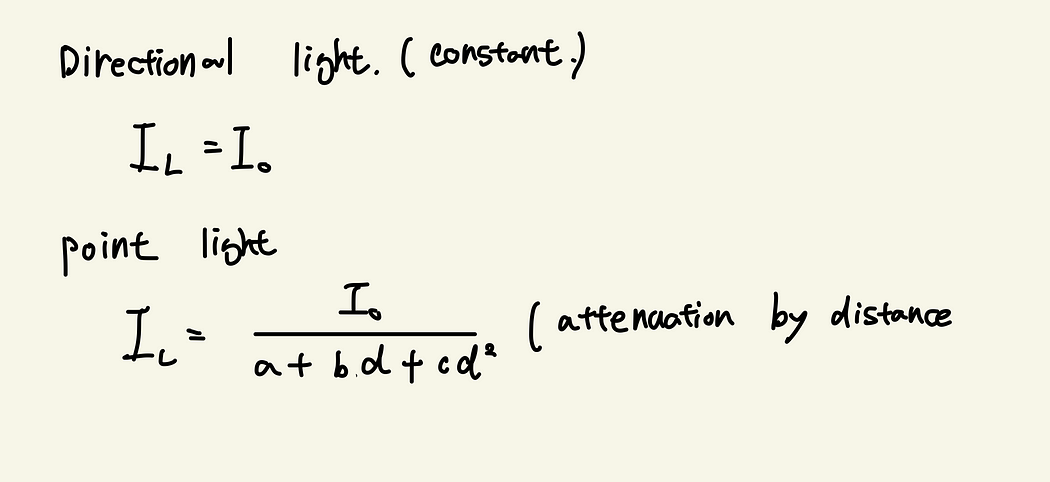
3. 移动光源

光源是其位置或方向受模型视图矩阵影响的几何对象。

如果我们将灯安装在汽车上，光源就会随着汽车移动。 （需要更新位置）

4. 材质属性

根据材质属性，相同的照明可以以不同的方式表示。

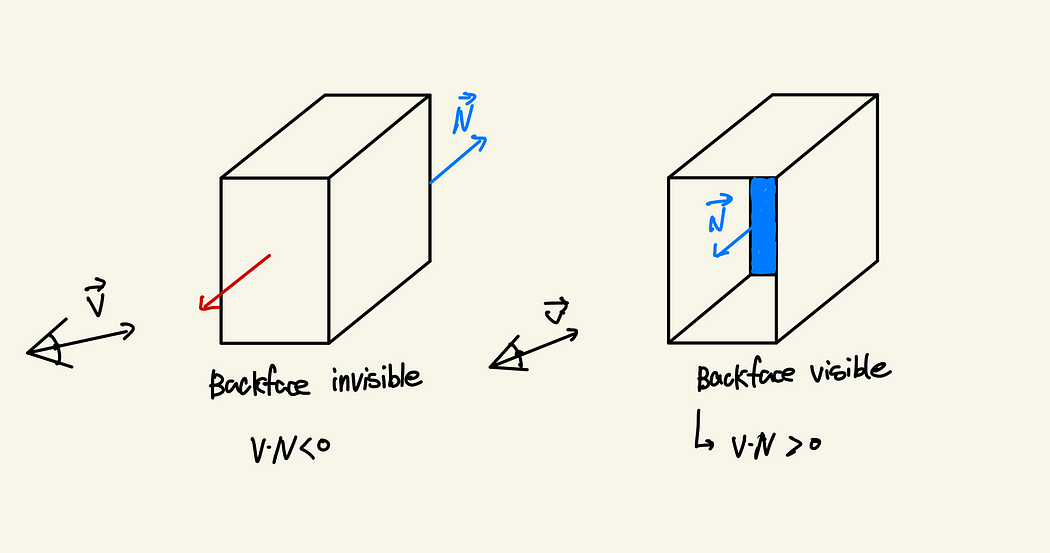
5. 背面可见性

大多数情况下，物体是不透明的，无法看到物体的背面。

但是，如果一个物体具有像镜子一样的透明面，则背面的法线向量将变得与正面的方向相似。也就是说，它是可见的。

我们也可以在着色器中处理这个问题。

Shader程序示例（Gouraud着色）

• 顶点着色器

in vec4 vPosition; 
in vec3 vNormal;
//using vPosition & vNormal attribute, we calculate this
out vec4 color; // vertex shade

// light and material properties
uniform vec4 ambientProduct, diffuseProduct, specularProduct
uniform mat4 modelView
uniform mat4 projection;
uniform vec4 lightPos;
uniform float shininess;

void main() 
{
  // Transform vertex position into eye coordinates.
  vec3 pos = (modelView * vPosition).xyz; // swizzling component;
  
  vec3 L = normalize(lightPos.xyz - pos);
  vec3 E = normalize(-pos);
  vec3 H = normalize(L+E);

  // Transform vertex normal into eye coordinates
  vec3 N = normalize(ModelView * vec4(vNormal, 0.0).xyz);

  // compute terms in illumination equation.
  // assume no atteunation
  float kd = max(dot(N,L), 0.0);
  vec4 diffuse = kd * diffuseProduct;
  float ks = pow(max(dot(N,H),0.0), shininess); // simplified phong model
  vec4 specular = ks * specularProduct;
  if(dot(L,N) < 0.0) specular = vec4(0.0,0.0,0.0, 1.0);
   
  // gl_Position is built-in uniform variable
  gl_Position = projection * modelView * vPosition;

  // output.
  color = ambientProduct + diffuse + specular;
  color.a = 1.0;
  
}

• 片段着色器

in vec4 color;

void main()
{
  gl_FragColor = color;
}

着色器中的纹理映射

应用纹理的三个基本步骤：

1. 在应用程序中指定纹理

• 读取或生成图像（例如读取png文件，自己生成深度图）
• 将其分配给纹理（此处应用最近邻/线性插值/MipMap 算法）
• 启用纹理

2. 给顶点指定纹理坐标

3. 指定纹理参数（包裹wrapping、过滤filtering）

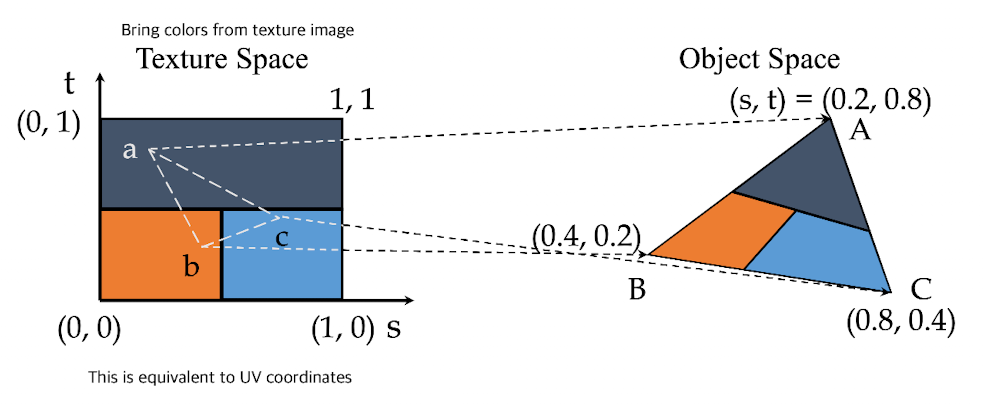
纹理如何映射到对象？

在 UV 坐标中，每个颜色信息都是针对每个位置定义的。

根据我们设置的纹理坐标，映射到相应的UV坐标并得到它的颜色。