复习记录
- 2.1 关系数据结构及形式化定义
- 2.1.1 关系
- 2.1.2 关系模式
- 2.1.3 关系数据库
- 2.2 关系操作
- 2.3 关系的完整性
- 2.4 关系代数
- 2.5 题目
2.1 关系数据结构及形式化定义
2.1.1 关系
一些概念
- 关系
R ( D 1 , D 2 , . . . , D n ) R(D_1,D_2,...,D_n) R(D1,D2,...,Dn)
D i D_i Di:域
R R R:关系名
n n n:关系的度
一个关系对应关系数据库中的一张表 - 元组
( d 1 , d 2 , . . . , d i d_1,d_2,...,d_i d1,d2,...,di),对应关系数据库中的一条记录 - 属性
关系中的列 - 码
- 候选码
能唯一标识一个元组的某一属性组,可有多个 - 主码
选一个候选码作为主码 - 全码
所有属性组合到一起构成一个码
- 主属性
候选码中包含的属性
非主/码属性:所有属性 - 主属性 - 基本关系的性质

其中6保证了1NF
2.1.2 关系模式
- 概念
关系模式是“型”,关系是值。一个是模子,一个是烧饼。对应一张表的表头。 - 形式化表示
R ( U , D , D O M , F ) R(U,D,DOM,F) R(U,D,DOM,F)
U U U:属性名的集合
D D D:U中属性所来自的域
D O M DOM DOM:属性向域的映像集合
F F F:属性间数据依赖关系的集合
简记为:
R ( U ) R(U) R(U), R ( A 1 , A 2 , . . . , A n ) R(A_1,A_2,...,A_n) R(A1,A2,...,An)
A i A_i Ai:属性名
D、DOM常直接说明为类型,长度 - 关系模式与关系的关系
型与值的关系。关系模式是静态的,关系是动态的。
2.1.3 关系数据库
在一个给定的应用领域中,所有关系的集合构成一个关系数据库
2.2 关系操作
- 5种基本操作:选择,投影,并,差,笛卡尔积
- 特点:操作的对象与结果都是集合
2.3 关系的完整性
-
实体完整性
主属性不能重复且非空,作为唯一性标识 -
参照完整性
类似外键约束
假设有关系:
R ( A ‾ , B , C ) R(\underline A,B,C) R(A,B,C)
S ( D ‾ , E , F ) S(\underline D,E,F) S(D,E,F)
C属性组的取值参照S中的D(即NULL,或D中的值),被参照的属性组必须是主码。 -
用户定义的完整性
用户自定义约束:唯一,非空…
2.4 关系代数
- 定义
关系代数是一种抽象的查询语言,它用对关系的运算来表达查询。运算对象是关系,运算结果也是关系。包含传统的集合运算符和专门的关系运算符。
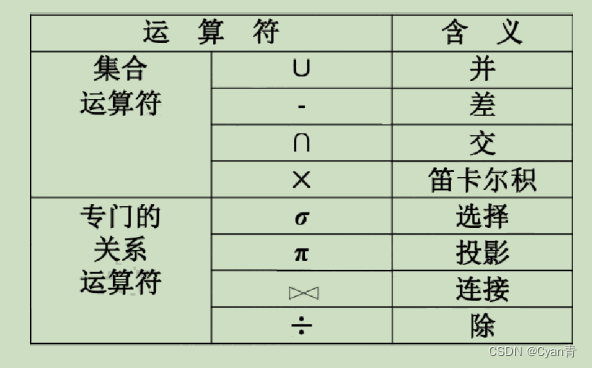
- 记号
R , t , t [ A i ] , 象集 Z x R,t,t[A_i],象集Z_x R,t,t[Ai],象集Zx
t:tuple,R中的一个元组
t [ A i ] t[A_i] t[Ai]:该元组在属性 A i A_i Ai上的分量
R(X, Z):
Z x Z_x Zx= { t [ Z ] ∣ t ∈ R , t [ X ] = x t[Z]| t {\in} R, t[X] = x t[Z]∣t∈R,t[X]=x}

- 专门的关系运算
- 选择
σ F ( R ) = { t ∣ t ∈ R , F ( t ) = T r u e } \sigma_{F}(R) = \{t | t \in R ,F(t) = True\} σF(R)={t∣t∈R,F(t)=True}
相当于where

- 投影
π A ( R ) = { t [ A ] ∣ t ∈ R } \pi_A(R) = \{t[A] | t \in R\} πA(R)={t[A]∣t∈R}
因为是集合操作,所以自动去重。
从列的角度进行运算

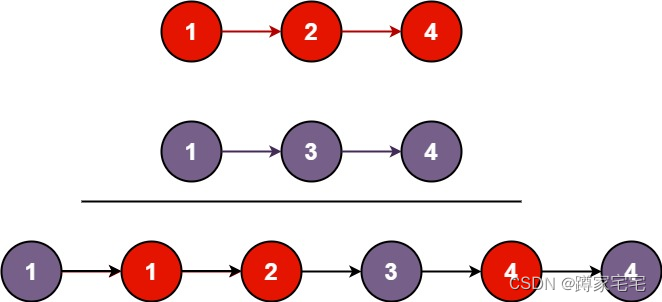
- 连接

等值连接:
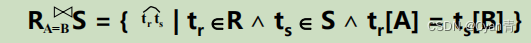
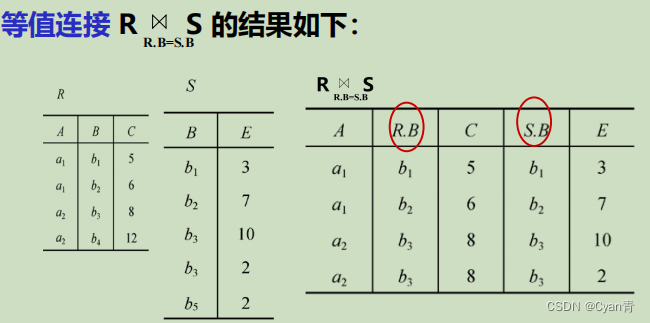
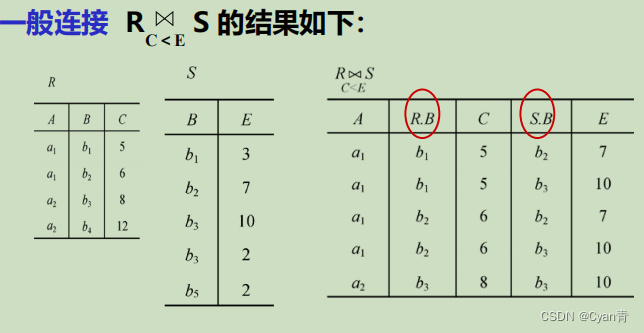
自然连接:
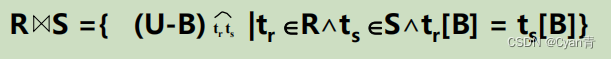
U为R,S所有的属性组,B为R,S共有的属性组。既筛选了重复行又取消了重复列。
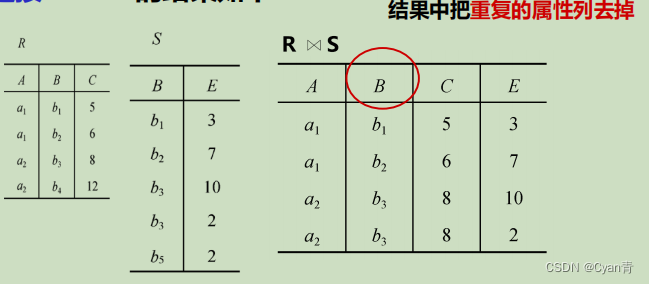
- 悬浮元组
两个关系R和S在做自然连接时,关系R中某些元组可能在S中不存在公共属性上值相等的元组,从而造成R中这些元组操作时被舍弃了,这些被舍弃的元组称为悬浮元祖。

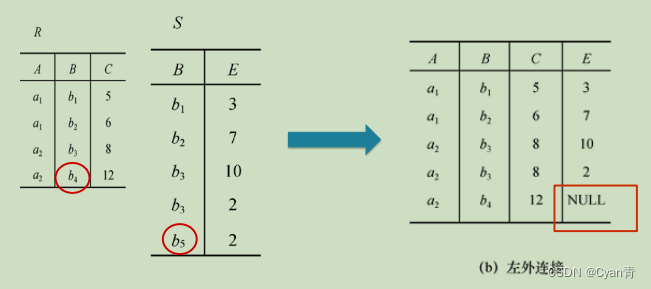
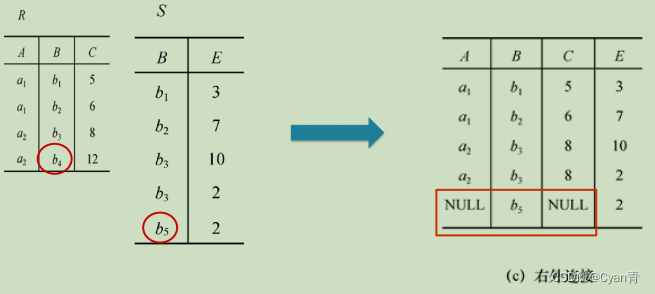
- 除





2.5 题目



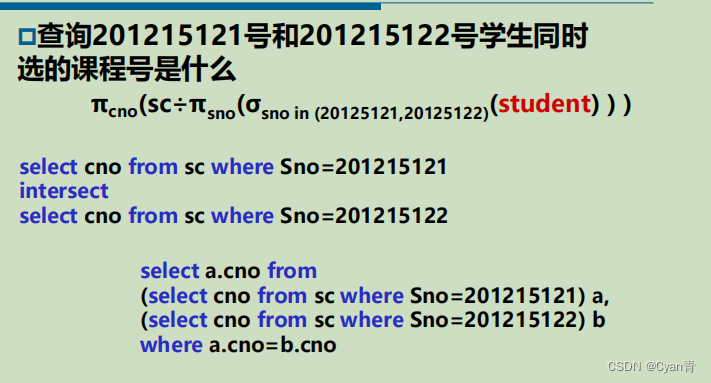
”同时“考虑除法