KMP算法应该是每一本《数据结构》书都会讲的,算是知名度最高的算法之一了,但很可惜,我大二那年压根就没看懂过~~~
之后也在很多地方也都经常看到讲解KMP算法的文章,看久了好像也知道是怎么一回事,但总感觉有些地方自己还是没有完全懂明白。这两天花了点时间总结一下,有点小体会,我希望可以通过我自己的语言来把这个算法的一些细节梳理清楚,也算是考验一下自己有真正理解这个算法。
KMP是三位大牛:D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。其中第一位就是《计算机程序设计艺术》的作者!!
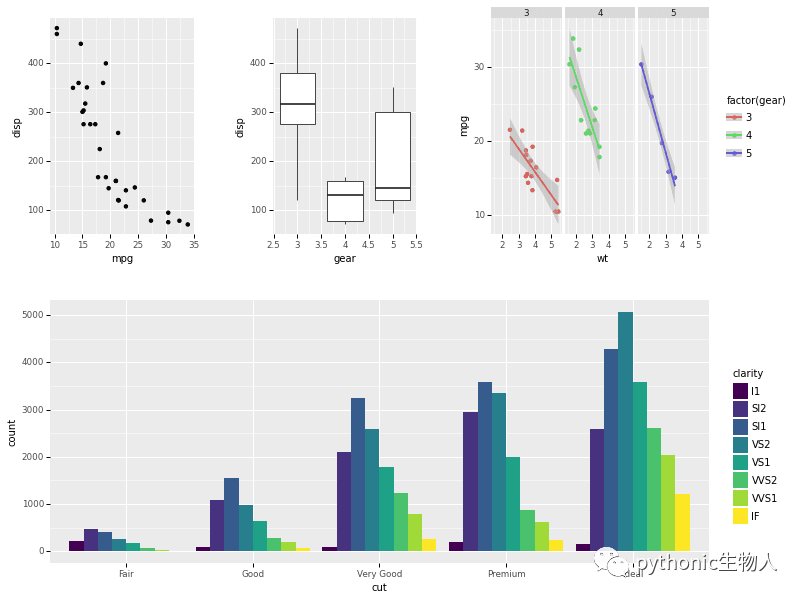
KMP算法要解决的问题就是在字符串(也叫主串)中的模式(pattern)定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字(接下来称它为P),如果它在一个主串(接下来称为T)中出现,就返回它的具体位置,否则返回-1(常用手段)。

1、首先,对于这个问题有一个很单纯的想法:
从左到右一个个匹配,如果这个过程中有某个字符不匹配,就跳回去,将模式串向右移动一位。这有什么难的?
我们可以这样初始化:

之后我们只需要比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动,如果不一致,如下图:

A和E不相等,那就把i指针移回第1位(假设下标从0开始),j移动到模式串的第0位,然后又重新开始这个步骤:

基于这个想法我们可以得到以下的程序:
/**
* 暴力破解法
@param ts 主串
@param ps 模式串
* @return 如果找到,返回在主串中第一个字符出现的下标,否则为-1
*/
public static int bf(String ts, String ps) {
char[] t = ts.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // 主串的位置
int j = 0; // 模式串的位置
while (i < t.length && j < p.length) {
if (t[i] == p[j]) { // 当两个字符相同,就比较下一个
i++;
j++;
} else {
i = i - j + 1; // 一旦不匹配,i后退
j = 0; // j归0
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}
上面的程序是没有问题的,但不够好!(想起我高中时候数字老师的一句话:我不能说你错,只能说你不对~~~)。
如果是人为来寻找的话,肯定不会再把i移动回第1位,因为主串匹配失败的位置前面除了第一个A之外再也没有A了,我们为什么能知道主串前面只有一个A?因为我们已经知道前面三个字符都是匹配的!(这很重要)。移动过去肯定也是不匹配的!有一个想法,i可以不动,我们只需要移动j即可,如下图:

上面的这种情况还是比较理想的情况,我们最多也就多比较了再次。但假如是在主串“SSSSSSSSSSSSSA”中查找“SSSSB”,比较到最后一个才知道不匹配,然后i回溯,这个的效率是显然是最低的。
大牛们是无法忍受“暴力破解”这种低效的手段的,于是他们三个研究出了KMP算法。其思想就如同我们上边所看到的一样:“利用已经部分匹配这个有效信息,保持i指针不回溯,通过修改j指针,让模式串尽量地移动到有效的位置。”
所以,整个KMP的重点就在于当某一个字符与主串不匹配时,我们应该知道j指针要移动到哪?
2、接下来我们自己来发现j的移动规律:

如图:C和D不匹配了,我们要把j移动到哪?显然是第1位。为什么?因为前面有一个A相同啊:

如下图也是一样的情况:
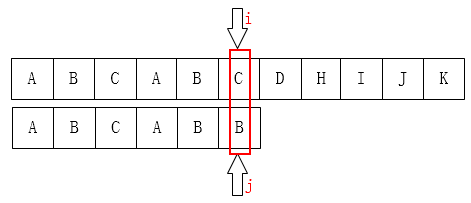
可以把j指针移动到第2位,因为前面有两个字母是一样的:
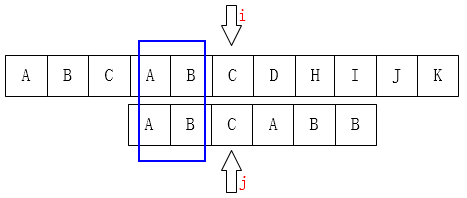
至此我们可以大概看出一点端倪,当匹配失败时,j要移动的下一个位置k。存在着这样的性质:最前面的k个字符和j之前的最后k个字符是一样的。
如果用数学公式来表示是这样的
P[0 ~ k-1] == P[j-k ~ j-1]
这个相当重要,如果觉得不好记的话,可以通过下图来理解:

弄明白了这个就应该可能明白为什么可以直接将j移动到k位置了。
因为:
当T[i] != P[j]时
有T[i-j ~ i-1] == P[0 ~ j-1]
由P[0 ~ k-1] == P[j-k ~ j-1]
必然:T[i-k ~ i-1] == P[0 ~ k-1]
公式很无聊,能看明白就行了,不需要记住。
这一段只是为了证明我们为什么可以直接将j移动到k而无须再比较前面的k个字符。
3、好,接下来就是重点了,怎么求这个(这些)k呢?
因为在P的每一个位置都可能发生不匹配,也就是说我们要计算每一个位置j对应的k,所以用一个数组next来保存,next[j] = k,表示当T[i] != P[j]时,j指针的下一个位置。
很多教材或博文在这个地方都是讲得比较含糊或是根本就一笔带过,甚至就是贴一段代码上来,为什么是这样求?怎么可以这样求?根本就没有说清楚。而这里恰恰是整个算法最关键的地方。
public static int[] getNext(String ps) {
char[] p = ps.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) {
next[++j] = ++k;
} else {
k = next[k];
}
}
return next;
}
这个版本的求next数组的算法应该是流传最广泛的,代码是很简洁。可是真的很让人摸不到头脑,它这样计算的依据到底是什么?
好,先把这个放一边,我们自己来推导思路,现在要始终记住一点,next[j]的值(也就是k)表示,当P[j] != T[i]时,j指针的下一步移动位置。
先来看第一个:当j为0时,如果这时候不匹配,怎么办?
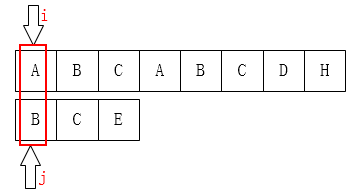
像上图这种情况,j已经在最左边了,不可能再移动了,这时候要应该是i指针后移。所以在代码中才会有next[0] = -1;这个初始化。
如果是当j为1的时候呢?

显然,j指针一定是后移到0位置的。因为它前面也就只有这一个位置了~~~
下面这个是最重要的,请看如下图:
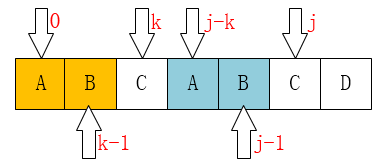

请仔细对比这两个图。
我们发现一个规律:
当P[k] == P[j]时,有next[j+1] == next[j] + 1
其实这个是可以证明的:
因为在P[j]之前已经有P[0 ~ k-1] == p[j-k ~ j-1]。(next[j] == k)
这时候现有P[k] == P[j],我们是不是可以得到P[0 ~ k-1] + P[k] == p[j-k ~ j-1] + P[j]。
即:P[0 ~ k] == P[j-k ~ j],即next[j+1] == k + 1 == next[j] + 1。
这里的公式不是很好懂,还是看图会容易理解些。
那如果P[k] != P[j]呢?比如下图所示:
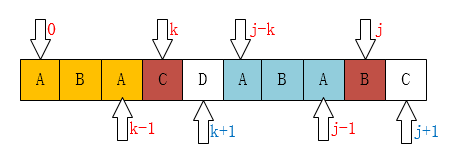
像这种情况,如果你从代码上看应该是这一句:k = next[k];为什么是这样子?你看下面应该就明白了。

现在你应该知道为什么要k = next[k]了吧!像上边的例子,我们已经不可能找到[ A,B,A,B ]这个最长的后缀串了,但我们还是可能找到[ A,B ]、[ B ]这样的前缀串的。所以这个过程像不像在定位[ A,B,A,C ]这个串,当C和主串不一样了(也就是k位置不一样了),那当然是把指针移动到next[k]啦。
有了next数组之后就一切好办了,我们可以动手写KMP算法了:
public static int KMP(String ts, String ps) {
char[] t = ts.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // 主串的位置
int j = 0; // 模式串的位置
int[] next = getNext(ps);
while (i < t.length && j < p.length) {
if (j == -1 || t[i] == p[j]) { // 当j为-1时,要移动的是i,当然j也要归0
i++;
++;
} else {
// i不需要回溯了
// i = i - j + 1;
j = next[j]; // j回到指定位置
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}
和暴力破解相比,就改动了4个地方。其中最主要的一点就是,i不需要回溯了。
4、最后,来看一下上边的算法存在的缺陷。
来看第一个例子:

显然,当我们上边的算法得到的next数组应该是[ -1,0,0,1 ]
所以下一步我们应该是把j移动到第1个元素咯:
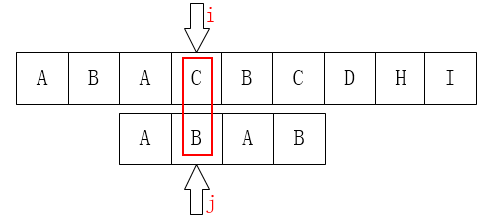
不难发现,这一步是完全没有意义的。因为后面的B已经不匹配了,那前面的B也一定是不匹配的,同样的情况其实还发生在第2个元素A上。
显然,发生问题的原因在于P[j] == P[next[j]]。
所以我们也只需要添加一个判断条件即可:
public static int[] getNext(String ps) {
char[] p = ps.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) {
if (p[++j] == p[++k]) { // 当两个字符相等时要跳过
next[j] = next[k];
} else {
next[j] = k;
}
} else {
k = next[k];
}
}
return next;
}
好了,至此。KMP算法也结束了。
很奇怪,好像不是很难的东西怎么就把我困住这么久呢?
仔细想想还是因为自己太浮躁了,以前总是草草应付,很多细节都没弄清楚,就以为自己懂了。结果就只能是似懂非懂的。要学东西真的需要静下心来。