🎇个人主页:Ice_Sugar_7
🎇所属专栏:初阶数据结构
🎇欢迎点赞收藏加关注哦!
文章目录
- 🍉前言
- 🍉链式结构
- 🍉遍历二叉树
- 🍌前序遍历
- 🍌中序遍历
- 🍌后序遍历
- 🍉计数
- 🍌求结点数
- 🍌求叶子结点数
- 🍌求第k层结点数
- 🍉树的深度
- 🍉查找结点
- 🍉构建二叉树
- 🍉销毁二叉树
- 🍉层序遍历
- 🍉判断是否为完全二叉树
- 🍌补充
- 🍉写在最后
🍉前言
在上一篇文章中我们讲了二叉树的顺序结构,但是普通二叉树因为结点不连续,没法使用顺序结构,这就需要使用链式结构进行存储。本文将讲解二叉树的链式结构及常见函数的实现
🍉链式结构
一个结点分为三个部分:存放当前结点的数值的数据域、分别指向左、右子树的指针
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
🍉遍历二叉树
二叉树有三种遍历方式,通过递归实现
需要根据使用场景选择不同的遍历方式
🍌前序遍历
先访问根结点,接着是左子树,最后访问右子树(这里的“访问”指的是把结点的数值打印出来)
采用递归,那就要将大问题拆分为小问题,直到问题无法再继续拆分
●现在要访问左子树,那可以把问题拆解为“依次访问它的根结点、左子树、右子树”,拆解若干次之后,会抵达叶子结点,再往下就是空结点了,此时没法继续拆解问题,也就是到达递归的终点了,需要回归了
●右子树也同理
void BinaryTreePrevOrder(BTNode* root) {
if (!root) {
cout << "NULL" << " "; //为了方便观察,所以把NULL也打印出来
return;
}
cout << root->_data << " ";
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
有了前序遍历作为参照,那中后序遍历也就很轻松就能写出来了,只要调整一下打印语句的位置就ok了,下面直接上代码
🍌中序遍历
void BinaryTreePrevOrder(BTNode* root) {
if (!root) {
cout << "NULL" << " "; //为了方便观察,所以把NULL也打印出来
return;
}
BinaryTreePrevOrder(root->_left);
cout << root->_data << " ";
BinaryTreePrevOrder(root->_right);
}
🍌后序遍历
void BinaryTreePrevOrder(BTNode* root) {
if (!root) {
cout << "NULL" << " "; //为了方便观察,所以把NULL也打印出来
return;
}
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
cout << root->_data << " ";
}
🍉计数
🍌求结点数
求结点数,可以转化为左子树结点数+右子树结点数+1(根结点本身),如果遇到空结点,那就返回0
int BinaryTreeSize(BTNode* root) {
if (!root)
return 0;
return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
🍌求叶子结点数
和求结点数差不多,不过多了一个判断是否为叶子结点的语句,如果是,就返回1
//左右结点都为空返回1
int BinaryTreeLeafSize(BTNode* root) {
if (!root)
return 0;
if (root->_left == NULL && root->_right == NULL)
return 1;
//不为空or只有一个子树为空
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
🍌求第k层结点数
这个的递归不太好找。
方法如下:
假设k为5,那么第k层相对于第一层就是第五层,而它相对第二层则是第四层,相对第三层是第三层……相对第五层就是第一层。也就是说要求第k层,实际上是求“第一层”的结点个数(有点像求一个数的阶乘时用到的递归思想)
int BinaryTreeLevelKSize(BTNode* root, int k) {
assert(k > 0); //确保k为正数
if (!root)
return 0;
if (k == 1) //此时已经递归到了第k层
return 1;
return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
🍉树的深度
深度是指从根结点到叶子结点的最长距离。这个问题可以拆解为求第二层的根结点到叶子结点的最长距离+1,再拆为第三层到叶子结点的最长距离+2……最后遇到空结点就可以停下来了
最后返回左子树和右子树二者深度的较大值
代码如下:
int BinaryTreeDepth(BTNode* root) {
if (!root)
return 0;
int LeftSize = BinaryTreeDepth(root->_left);
int RightSize = BinaryTreeDepth(root->_right);
return LeftSize > RightSize ? LeftSize + 1 : RightSize + 1;
}
🍉查找结点
要在二叉树里面查找值为x的结点。每次递归先找左子树,找到就返回,找不到就去找右子树。
下面两个条件满足其一,递归终止:①到空结点时返回NULL;②找到值为x的结点就返回该结点
代码如下:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
if (!root)
return NULL;
if (root->_data == x)
return root;
BTNode* ret = BinaryTreeFind(root->_left, x);
if (ret) //如果左子树找到指定结点,就不用找右子树了
return ret;
return BinaryTreeFind(root->_right, x);
}
🍉构建二叉树
现在已知一个数组,它是某二叉树前序遍历的结果,该数组会用#表示空结点,现在要我们通过这个数组来构建原二叉树
●通过递归来构建。每次递归时数组当前位置的元素如果不为#,就创建一个结点,然后将它和双亲结点连起来。
●既然要让结点间能够连接起来,那函数就要返回结点或者NULL。这样在递归的过程中可以将新创建的结点或者NULL和双亲结点连接起来
●递归的停止条件就是遇到#,此时返回NULL,
BTNode* BinaryTreeCreate(BTDataType* a, int n, int pi) { //n:数组大小 pi:指向数组下标
if (a[pi] == '#') {
++pi;
return NULL;
}
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
node->_data = a[pi++]; //数组赋值给node之后记得++
node->_left = BinaryTreeCreate(a, n, pi); //连接左子树
node->_right = BinaryTreeCreate(a, n, pi); //连接右子树
return node; //返回根结点
}
这里要说一下这个pi,因为我们使用递归而非迭代,需要知道数组下标(即递归到哪个元素了),所以要传下标
🍉销毁二叉树
要采用后序遍历销毁结点,如果采用前序或中序,根结点都不是最后销毁的,这样会导致无法找到某一边的子树。比如采用中序,销毁左子树后把根结点给销毁了,那就没法找到右子树了
void BinaryTreeDestory(BTNode** root) {
assert(root);
if (*root == NULL)
return;
BinaryTreeDestory(&(*root)->_left);
BinaryTreeDestory(&(*root)->_right);
free(*root);
*root = NULL;
}
🍉层序遍历
前面讲的前、中、后序遍历都属于深度优先遍历,以前序遍历为例,会先递推到最左下的结点,然后才回归,这是一个纵向的过程。
而层序遍历又称为广度优先遍历,顾名思义,就是一层一层遍历。这种遍历需要使用队列
具体的过程为:先让根结点入队,标记为队首front,然后将它的左右子树根结点入队(前提是结点不为空,如果为空那就不用入),再让队头的根结点出队,子树的根结点成为新的队头。
重复上面这个过程,直到队列为空
举个栗子:
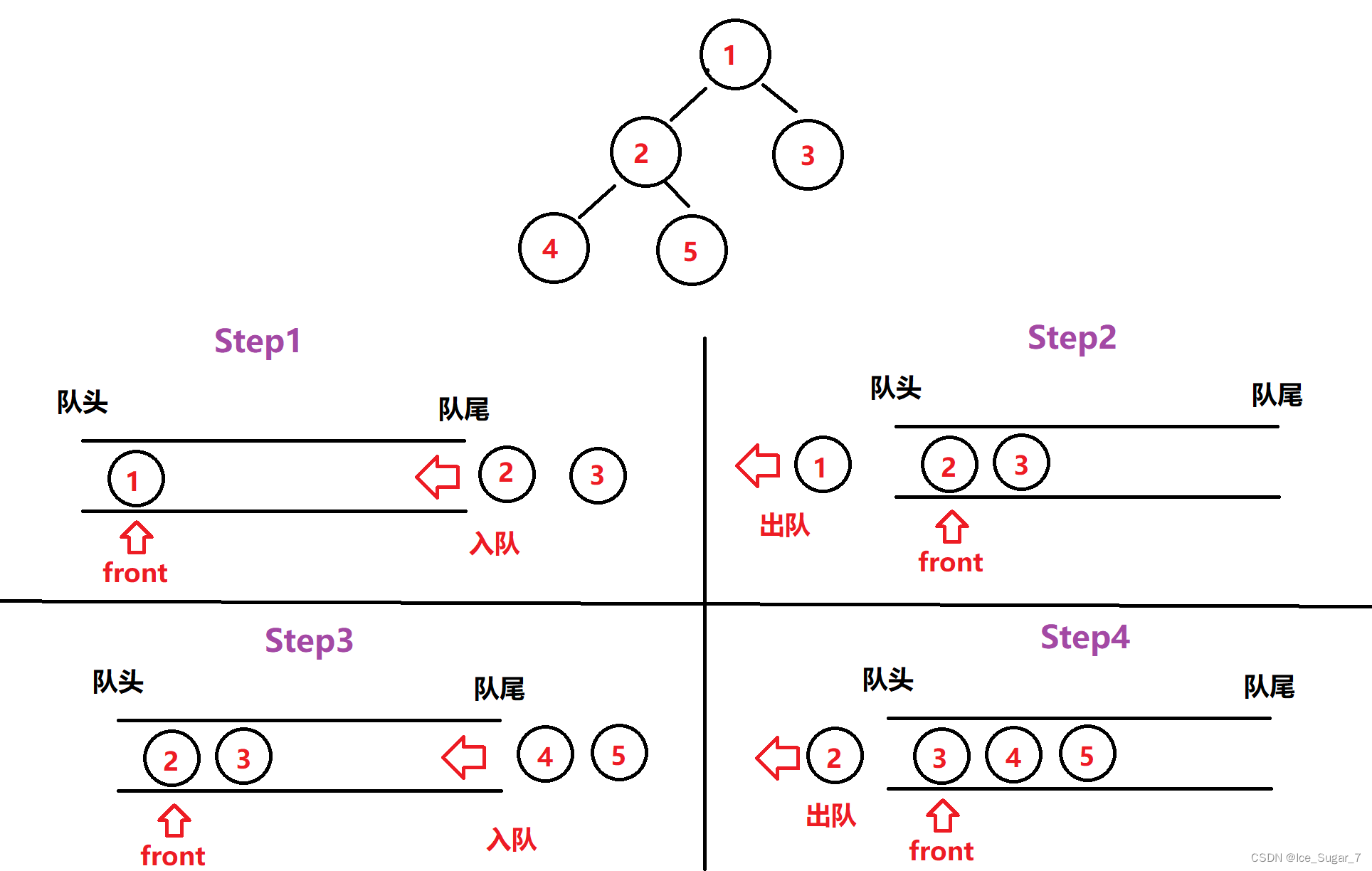
代码如下:
void BinaryTreeLevelOrder(BTNode* root) {
if (!root)
return;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
QDataType front = QueueFront(&q); //队首元素
cout << QueueFront(&q)->_data << endl;
QueuePop(&q); //队首元素出队 然后要让它的左右子树入队
if (root->_left)
QueuePush(&q, front->_left);
if (root->_left)
QueuePush(&q, front->_right);
}
QueueDestroy(&q);
}
🍉判断是否为完全二叉树
完全二叉树的特点就是结点连续,根据这个性质,我们采用层序遍历,不过这次层序遍历需要把空结点也入队。如果遇到空结点时后面的结点也全为空,那就是完全二叉树;反之,如果后面还有非空结点,那就不是
简而言之,我们要判断front为空结点时队列剩下的元素是否全为空
代码如下:
bool BinaryTreeComplete(BTNode* root) {
if (!root)
return true;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
BTNode* front = root;
while (!QueueEmpty(&q)){
front = QueueFront(&q);
if (front == NULL) //队首是空结点,就是遇到的第一个空结点,跳出循环
break;
//空结点也要入队
QueuePush(&q, front->_left);
QueuePush(&q, front->_right);
QueuePop(&q); //队首元素出队
}
//到这里的时候说明已经遇到空结点
//接下来要排查剩下的结点,看看是否有非空结点
while (!QueueEmpty(&q)) {
front = QueueFront(&q);
QueuePop(&q);
if (front) { //若遇到不为空的结点,说明不是完全二叉树
QueueDestroy(&q);
return false;
}
}
//到这里说明全部都是空结点,那就是完全二叉树了
QueueDestroy(&q);
return true;
}
🍌补充
while (!QueueEmpty(&q)) {
front = QueueFront(&q);
QueuePop(&q);
if (front) {
QueueDestroy(&q);
return false;
}
}
我们已经将队首的结点pop掉,那后面的if语句还能否访问front?
答案是可以。因为front保存队首结点的值,而这个值是二叉树结点的地址,即指向二叉树的结点。(刚才上面那个图是为了方便理解,所以才把front的箭头指向队首)pop掉队首结点并不会影响树的结点,所以还是可以访问的
🍉写在最后
以上就是本篇文章的全部内容,如果你觉得本文对你有所帮助的话,那不妨点个小小的赞哦!(比心)







![[足式机器人]Part4 南科大高等机器人控制课 CH10 Bascis of Stability Analysis](https://img-blog.csdnimg.cn/direct/4d9db554c7ce4010b525499f4ff67684.png#pic_center)