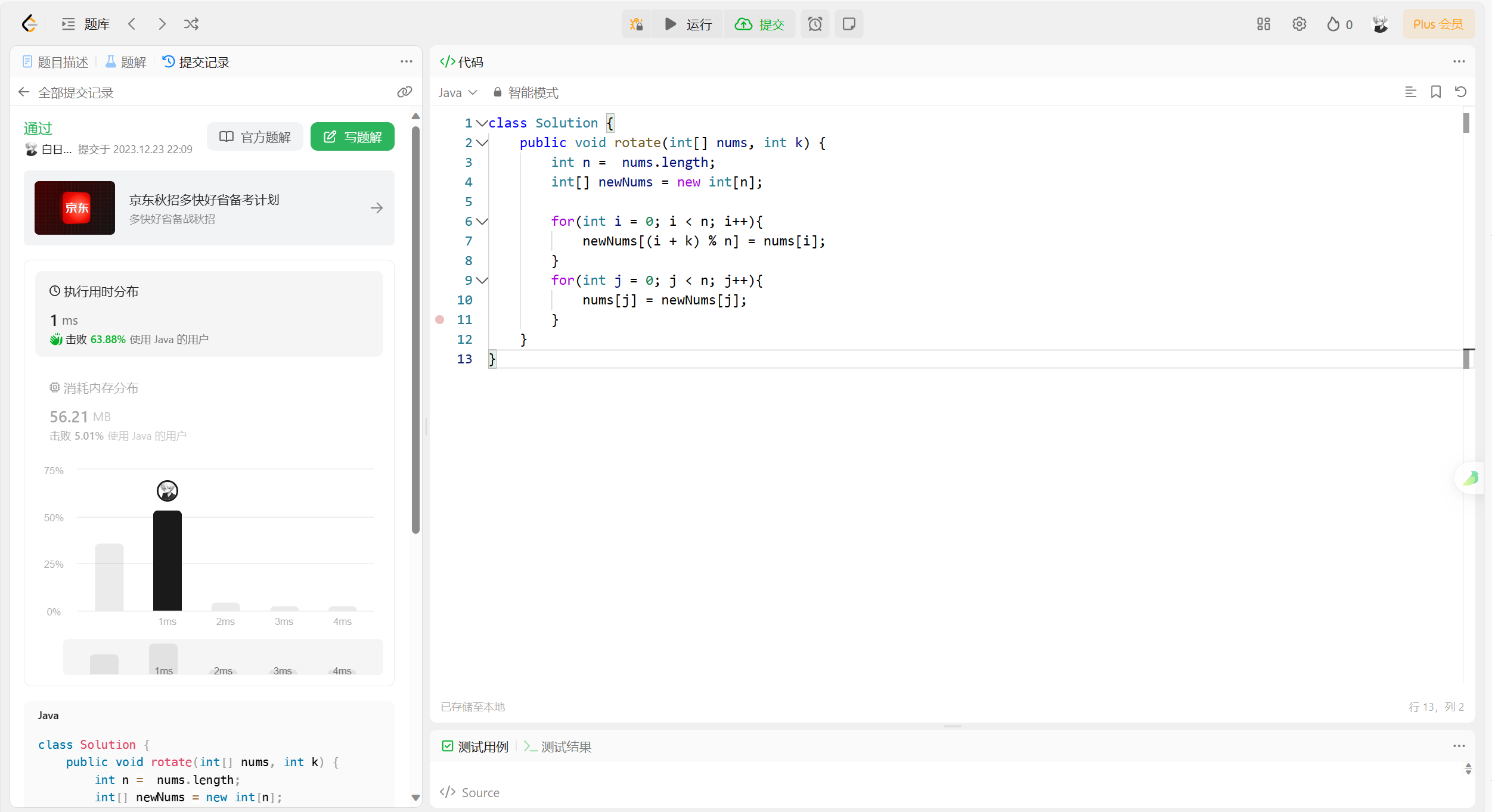
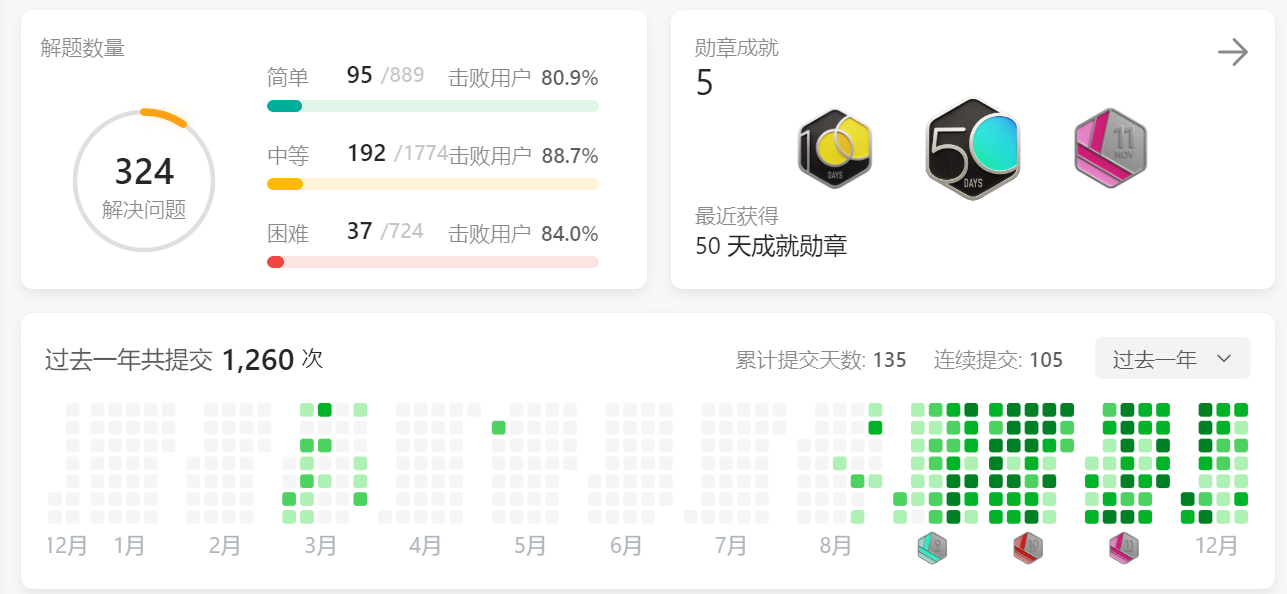
完全背包:
首先01背包的滚动数组中的解法是内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}同时找到规律,如果存在后序遍历(比如01背包的滚动数组)的话,两个for循环的顺序就不可以变,但如果都是正序的话,两个for循环的顺序就可以进行改变。
518.零钱兑换||
题解复盘:
1)dp数组的含义:dp[j]:凑成总金额j的货币组合数为dp[j]
2)数组的递推公式:dp[j] += dp[j - coins[i]];
3)初始化:
dp[0] = 1 ;
下标非0的dp[j]初始化为0,dp[0]=1还说明了一种情况:如果正好选了coins[i]后,也就是j-coins[i] == 0的情况表示这个硬币刚好能选,此时dp[0]为1表示只选coins[i]存在这样的一种选法。
4)确定遍历顺序:
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品
5)举例推导dp数组

大概的数字变化情况,coins[1]的dp[2] = coins[0]那排的dp[2] + coins[1]的dp[0],不选coins[1]的方法数加上选coins[1]的方法数.
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] = 1;
for(int i = 0;i<coins.length;i++){
for(int j=coins[i];j<amount+1;j++ ){
if(j-coins[i]<0){
dp[j] = dp[j];
}else{
dp[j] = dp[j]+dp[j-coins[i]];
}
}
}
return dp[amount];
}
}377.组合总和IV
这道题相较于上一道感觉是由求组合数变为了求排列数。
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
Arrays.sort(nums);
if(nums[0]<target){
dp[0] = 1;
}else{
dp[0] = 0;
}
for(int i = nums[0];i<target+1;i++){
for(int j = 0;j<nums.length;j++){
if(i-nums[j]>=0){
dp[i] = dp[i]+dp[i-nums[j]];
}else{
dp[i] = dp[i];
}
}
}
return dp[target];
}
}70. 爬楼梯(进阶版)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数
初始思路:
之前的爬楼梯每次爬1,2个台阶,dp(3) = dp(1)+dp(2)
由此推断每次爬1 <= m,dp(m+1) = dp(m)+dp(m-1)+...+dp(1)
分析动态规划五部曲:
(1)dp数组的含义:dp[j] 爬j阶台阶的方法数。
(2)dp的递推公式:
dp[n] = dp[n-m]+dp[n-m+1]+...+dp[n-1];
(3) 初始化:
dp[1] = 1;
dp[2] = 2;
dp[3] = dp[2]+dp[1]+1;
dp[4] = dp[3]+dp[2]+dp[1]+1;
dp[0] = 1;
dp[1] = dp[1]+dp[0];
dp[2] = dp[2]+dp[1]+dp[0];
(4)循环方式,先背包容量再物品,这样每一个容量都可以遍历一次所需要的物品
(5)举例:
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static int climbStairs(int n, int m) {
int[] dp = new int[n + 1];
Arrays.fill(dp, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (i - j >= 0) {
dp[i] += dp[i - j];
}
}
}
return dp[n];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
System.out.println(climbStairs(n, m));
}
}可以理解题解,但是卡码网会超时不知道为什么。
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
初始思路&&题解复盘:
感觉是在完全背包的基础上变为了最少的硬币个数。之前是由小数开始遍历,如果要是最少的硬币个数感觉从大数开始遍历比较好?
动态规划五部曲:
1.dp数组的定义
dp[j]组成j元所需要的最少硬币数
2.递归数组
dp[j] = Math.min(dp[j],dp[j-coins[i]]+1)
3.初始化(这里没想到)
dp[0] = 0;
dp[i] = MAX_VALUE;
4.遍历顺序
考虑到组合问题,所以先循环物品,再循环背包
只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
if (dp[j - coins[i]] != max) {
//选择硬币数目最小的情况
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}5.推导
所以这道题目非常关键的地方一个是注意初始化,一个是只有满足条件时,该位的数值才发生更新。
279.完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
初始思路:
由题意可知,这道题需要我们自己构建coins数组,如果这个数小于16,那么我们的数组就只需要装1,4,9,剩下的步骤同上一题一样,注意处理一些较少数目的特殊情况。
class Solution {
public int numSquares(int amount) {
if(amount<4){return amount;}
int n = 0;
for(int i = 0;i<amount;i++){
if(i*i>amount){
n=i-1;
break;
}
}
int[] coins = new int[n];
for(int i = 0;i<coins.length;i++){
coins[i] = (i+1)*(i+1);
}
int[] dp = new int[amount+1];
dp[0] = 0;
for(int i = 1;i<amount+1;i++){
dp[i] = Integer.MAX_VALUE;
}
for(int i = 0;i<coins.length;i++){
for(int j = coins[i];j<amount+1;j++){
dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);
}
}
//System.out.println(Arrays.toString(dp));
return dp[amount];
}
}题解复盘:
class Solution {
// 版本一,先遍历物品, 再遍历背包
public int numSquares(int n) {
int max = Integer.MAX_VALUE;
int[] dp = new int[n + 1];
//初始化
for (int j = 0; j <= n; j++) {
dp[j] = max;
}
//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。
//Arrays.fill(dp, Integer.MAX_VALUE);
//当和为0时,组合的个数为0
dp[0] = 0;
// 遍历物品
for (int i = 1; i * i <= n; i++) {
// 遍历背包
for (int j = i * i; j <= n; j++) {
//if (dp[j - i * i] != max) {
dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
//}
//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。
}
}
return dp[n];
}
}一个完美的递推公式:dp[j] = Math.min(dp[j], dp[j - i * i] + 1)



![[足式机器人]Part4 南科大高等机器人控制课 CH10 Bascis of Stability Analysis](https://img-blog.csdnimg.cn/direct/4d9db554c7ce4010b525499f4ff67684.png#pic_center)