本题要求你从任意给定的两个 1 位数字 a1​ 和 a2​ 开始，用乘法口诀生成一个数列 {an​}，规则为从 a1​ 开始顺次进行，每次将当前数字与后面一个数字相乘，将结果贴在数列末尾。如果结果不是 1 位数，则其每一位都应成为数列的一项。

输入格式：

输入在一行中给出 3 个整数，依次为 a1​、a2​ 和 n，满足 0≤a1​,a2​≤9，0<n≤103。

输出格式：

在一行中输出数列的前 n 项。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

2 3 10

输出样例：

2 3 6 1 8 6 8 4 8 4

样例解释：

数列前 2 项为 2 和 3。从 2 开始，因为 2×3=6，所以第 3 项是 6。因为 3×6=18，所以第 4、5 项分别是 1、8。依次类推…… 最后因为第 6 项有 6×8=48，对应第 10、11 项应该是 4、8。而因为只要求输出前 10 项，所以在输出 4 后结束。

---

 

 

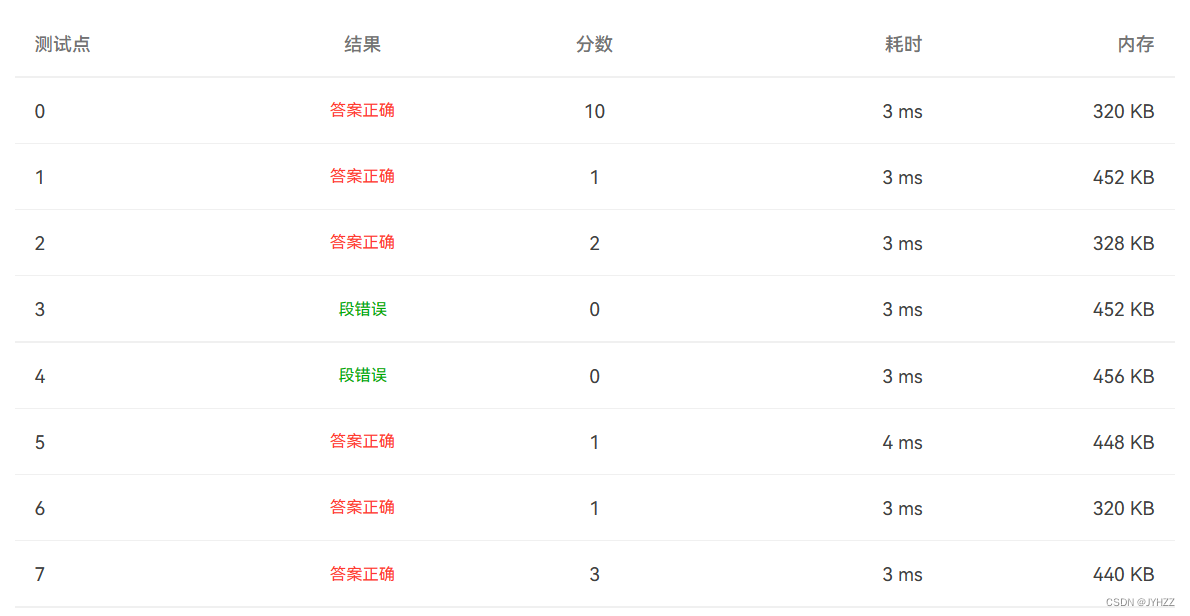
代码：部分通过（下面有已改正的代码）

#include<iostream>
#include<string.h>
#include<string>
using namespace std;

int main()
{
	int a1, a2, n;
	cin >> a1 >> a2 >> n;

	int array[1000];

	array[0] = a1;
	array[1] = a2;

	int temp;   //用来保存两数相乘的结果
	int flag = 1;
	int r = 2;
	for (int i = 0; flag; i++) {
		temp = array[i] * array[i + 1];
        
		if (temp > 9) {//如果temp不是0-9范围的数，就得拆分每一位
			int s[1000];
			int length = 0;
			int p;
			while (temp != 0) {
				p = temp % 10;
				temp = temp / 10;
				s[length++] = p;
			}

			if (length + r > n) {
				for (int k = length - 1; r != n; k--) {
					array[r++] = s[k];
				}
			}
			else {
				for (int k = length - 1; k >= 0; k--) {
					array[r++] = s[k];
				}
			}
		}
		else {
			array[r++] = temp;
		}

		if (r == n) {
			break;
		}

	}

	for (int i = 0; i < n; i++) {
		if (flag) {
			cout << array[i];
			flag = 0;
		}
		else {
			cout << " " << array[i];
		}
	}


	return 0;
}

改正：

我一开始的思路是如果相乘的结果大于9的话，拆分。

但是拆分的结果在最后可能会超出范围，最后还剩下一个位置，但是我们算得的相乘结果是两位数，比如这样：

n=3，a1=8,a2=9

相乘的结果是72，我们输出8，9，7。

就是这里导致了错误，其实没必要严丝合缝的保证算到n，每次循环判断的时候如果r>=n就行

if (length + r > n) {
	for (int k = length - 1; r != n; k--) {
		array[r++] = s[k];
	}
}
else {
	for (int k = length - 1; k >= 0; k--) {
		array[r++] = s[k];
	}
}

if (r == n) {
	break;
}

正确的代码：

#include<iostream>

using namespace std;

int main()
{
	int a1, a2, n;
	cin >> a1 >> a2 >> n;

	int array[1000];

	array[0] = a1;
	array[1] = a2;

	int temp; //用来保存两数相乘的结果
	int flag = 1;
	int r = 2;
	for (int i = 0; flag; i++) {
		temp = array[i] * array[i + 1];

		if (temp > 9) {//如果temp不是0-9范围的数，就得拆分每一位
			int s[1000];
			int length = 0;
			int p;
			while (temp != 0) {
				p = temp % 10;
				temp = temp / 10;
				s[length++] = p;
			}

			for (int k = length - 1; k >= 0; k--) {
				array[r++] = s[k];
			}
			
		}
		else {
			array[r++] = temp;
		}

		if (r >= n) {
			break;
		}

	}

	for (int i = 0; i < n; i++) {
		if (flag) {
			cout << array[i];
			flag = 0;
		}
		else {
			cout << " " << array[i];
		}
	}


	return 0;
}

---

继续看看别人的代码：

这个代码的思路和我的差不多一模一样，但是代码量比我少了将近一半，因为他注意到了这个：

 由于是乘法口诀表，所以最大为9×9=81，不可能出现三位数以上。

所以在处理两数相乘的结果为两位数时，比我的简洁很多

#include<stdio.h>
int main()
{
	int a1, a2, n, count = 3, num[1005], i, j, sum;
    scanf("%d %d %d", &a1, &a2, &n);
    num[1] = a1, num[2] = a2;
	for (i = 1; i <= n; i++)
	{
		sum = num[i] * num[i + 1];
		if (sum < 10)
		{
			num[count++] = sum;
		}
		else
		{
			num[count++] = sum / 10;
			num[count++] = sum % 10;
		}
		if (count > n)
			break;
	}
	printf("%d", a1);
	for (j = 2; j <= n; j++) 
	{
		printf(" %d", num[j]);
	}
    return 0;
}