松弛方法

1. 学习准则

• 在感知函数准则中, 目标函数中采用了 $-{\mathbf{a}}^T\mathbf{y}$ 的形式。实际上有很多其它准则也可以用于感知函数的学习。
• 线性准则
  $$J_p(\mathbf{a})=\sum _{\mathbf{y}\in Y}\left(-{\mathbf{a}}^T\mathbf{y}\right)$$
• 平方准则
  $$J_q(\mathbf{a})=\sum _{\mathbf{y}\in Y}{\left({\mathbf{a}}^T\mathbf{y}\right)}^2$$
• 松弛准则
  $$J_r(\mathbf{a})=\frac{1}{2}\sum _{\mathbf{y}\in Y}\frac{{\left({\mathbf{a}}^T\mathbf{y}-b\right)}^2}{\Vert \mathbf{y}{\Vert }^2}$$
• 线性准则的目标函数是分段线性的, 因此其梯度是不连续的。
• 平方准则的梯度是连续的, 但目标函数过于平滑, 收敛速度很慢（达到目标函数为零的区域的路径很平缓）。同时, 目标函数过于受到最长样本的影响。
• $J_r(\mathrm{a})$ 则避免了这些缺点。$J_r$ (a) 最终达到零。此时对所有的 $\mathbf{y},{\mathbf{a}}^T\mathbf{y}>b$, 则意味着集合 $Y$ 是空集。
  梯度：
  $$\frac{\partial J_r(\mathbf{a})}{\partial \mathbf{a}}=\sum _{\mathbf{y}\in Y}\frac{{\mathbf{a}}^T\mathbf{y}-b}{\Vert \mathbf{y}{\Vert }^2}\mathbf{y}$$
  权重更新准则：
  $${\mathbf{a}}_{k+1}={\mathbf{a}}_k-{\eta }_k\sum _{\mathbf{y}\in Y}\frac{{\mathbf{a}}^T\mathbf{y}-b}{\Vert \mathbf{y}{\Vert }^2}\mathbf{y}$$

• 每一步权重更新都要重新计算错误样本集，而且要用到错误样本集里面的所有样本
• 单样本松弛算法更新准则
  $${\mathbf{a}}_{k+1}={\mathbf{a}}_k-{\eta }_k\frac{{\mathbf{a}}_k^T{\mathbf{y}}^k-b}{{\Vert {\mathbf{y}}^k\Vert }^2}{\mathbf{y}}^k={\mathbf{a}}_k-{\eta }_k\frac{{\mathbf{a}}_k^T{\mathbf{y}}^k-b}{\Vert {\mathbf{y}}^k\Vert }\frac{{\mathbf{y}}^k}{\Vert {\mathbf{y}}^k\Vert }$$
  
  
  
• 单样本松弛法的收敛性（设 $\mathbf{a}$ 是一个解向量, 因此对任意 ${\mathbf{y}}_i$, 有 ${\mathbf{a}}^T{\mathbf{y}}_i>b$）
  $$\begin{array}{c}{\Vert {\mathbf{a}}_{k+1}-\mathbf{a}\Vert }^2={\Vert {\mathbf{a}}_k-\mathbf{a}\Vert }^2-2\eta \frac{b-{\mathbf{a}}_k^T{\mathbf{y}}^k}{{\Vert {\mathbf{y}}^k\Vert }^2}{\left(\mathbf{a}-{\mathbf{a}}_k\right)}^T{\mathbf{y}}^k+{\eta }^2\frac{{\left(b-{\mathbf{a}}_k^T{\mathbf{y}}^k\right)}^2}{{\Vert {\mathbf{y}}^k\Vert }^2}\\ {\left(\mathbf{a}-{\mathbf{a}}_{k+1}\right)}^T{\mathbf{y}}^k={\mathbf{a}}^T{\mathbf{y}}^k-{\mathbf{a}}_{k+1}^T{\mathbf{y}}^k>b-{\mathbf{a}}_{k+1}^T{\mathbf{y}}^k\\ \Rightarrow {\Vert {\mathbf{a}}_{k+1}-\mathbf{a}\Vert }^2<{\Vert {\mathbf{a}}_k-\mathbf{a}\Vert }^2-\eta (2-\eta )\frac{{\left(b-{\mathbf{a}}_k^T{\mathbf{y}}^k\right)}^2}{{\Vert {\mathbf{y}}^k\Vert }^2}\end{array}$$
  如果$0<\eta <2$，则${\Vert {\mathbf{a}}_{k+1}-\mathbf{a}\Vert }^2<{\Vert {\mathbf{a}}_k-\mathbf{a}\Vert }^2$

最小平方误差（MSE）准则函数

• 对两类分类问题, 感知准则函数是寻找一个解向量 $\mathbf{a},$, 对所有样本 ${\mathbf{y}}_i$, 满足 ${\mathbf{a}}^T{\mathbf{y}}_i>0,i=1,2,\dots n$ 。或者说, 求解一个不等式组, 使满足 ${\mathbf{a}}^T{\mathbf{y}}_i>0$ 的数目最大, 从而错分样本最少。
• 将不等式约束改为等式：
  $${\mathbf{a}}^T{\mathbf{y}}_i=b_i>0$$
  其中, $b_i$ 是任意给定的正常数, 通常取 $b_i=1$, 或者 $b_i=$ $n_j/n$ 。 其中 $n_j,j=1$或$2$, 为属于第 $j$ 类样本的总数, 且 $n_1+n_2=n$
• 可得一个线性方程组 $\mathbf{Ya}=\mathbf{b}$
  $$\left(\begin{array}{cccc}{y}_{10}& y_{11}& \cdots & y_{1d}\\ y_{20}& y_{21}& \cdots & y_{2d}\\ ⋮& ⋮& & ⋮\\ ⋮& ⋮& & ⋮\\ y_{n0}& y_{n1}& \cdots & y_{nd}\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ ⋮\\ a_d\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ ⋮\\ b_d\end{array}\right)$$
• 如果 $\mathbf{Y}$ 可逆, 则 $\mathbf{a}={\mathbf{Y}}^{-1}\mathbf{b}$
• 但通常情形下样本数远大于特征数 $n\gg d+1$, 求不出逆矩阵；因此考虑定义一个误差向量 $\mathbf{e}=\mathbf{Ya}-\mathbf{b}$, 并使误差向量最小
• 平方误差准则函数：
  $$J_s(\mathbf{a})=\Vert \mathbf{e}{\Vert }^2=\Vert \mathbf{Ya}-\mathbf{b}{\Vert }^2=\sum _{i=1}^n{\left({\mathbf{a}}^T{\mathbf{y}}_i-b_i\right)}^2$$
  求偏导数：
  $$\frac{\partial J_s(\mathbf{a})}{\partial \mathbf{a}}=\sum _{i=1}^{n}2\left({\mathbf{a}}^T{\mathbf{y}}_i-b_i\right){\mathbf{y}}_i=2{\mathbf{Y}}^T(\mathbf{Ya}-\mathbf{b})$$
  令偏导数为 $0$
  $${\mathbf{Y}}^T\mathbf{Ya}={\mathbf{Y}}^T\mathbf{b},\Rightarrow \mathbf{a}={\left({\mathbf{Y}}^T\mathbf{Y}\right)}^{-1}{\mathbf{Y}}^T\mathbf{b}={\mathbf{Y}}^{+}\mathbf{b}$$
  矩阵论告诉我们 ${\mathbf{Y}}^T\mathbf{Y}$ 一定是可逆的（我记得是在值空间零空间那边，但是我已经忘了ಥ_ಥ）；${\mathbf{Y}}^{+}$即为 $\mathbf{Y}$ 的伪逆，实际计算常用（不知道为什么）
  $${{\mathbf{Y}}^{+}\approx {\left({\mathbf{Y}}^T\mathbf{Y}+\epsilon \mathbf{I}\right)}^{-1}{\mathbf{Y}}^T|}_{\epsilon \to 0}$$
• 计算伪逆需要求矩阵的逆, 计算复杂度高。如果原始样本的维数很高, 比如 $d>5000$, 将十分耗时
• 采用梯度下降法: ${\mathbf{a}}_{k+1}={\mathbf{a}}_k+{\eta }_k{\mathbf{Y}}^T\left(\mathbf{b}-\mathbf{Y}{\mathbf{a}}_k\right)$
• 梯度下降法得到的 ${\mathbf{a}}_{k+1}$ 将收敛于一个解, 该解满足方程: ${\mathbf{Y}}^T(\mathbf{b}-\mathbf{Ya})=0$
• 也可以采用序列更新方法, 此方法需要的计算存储量会更小:
  $${\mathbf{a}}_{k+1}={\mathbf{a}}_k+{\eta }_k\left(b_k-{\left({\mathbf{a}}_k\right)}^T{\mathbf{y}}^k\right){\mathbf{y}}^k$$
• 序列最小平方更新方法
  
• Widrow-Hoff 要求更正不相等情形: ${\left({\mathbf{a}}_k\right)}^T{\mathbf{y}}^k\ne b_k$ 。但是, 实际上, 满足 ${\left({\mathrm{a}}_k\right)}^T{\mathbf{y}}^k=b_k$ 几乎是不可能的。因此, 迭代将会无穷次进行下去。所以要求 ${\eta }_k$ 需要随着 $k$ 的增加而逐渐减小, 以保证算法的收敛性。一般来讲, 实际计算中取: ${\eta }_k=$ ${\eta }_1/k$
• 相对于感知器准则, 最小平方准则方法可能并不收敛于可分超平面, 即使该平面是存在的
  
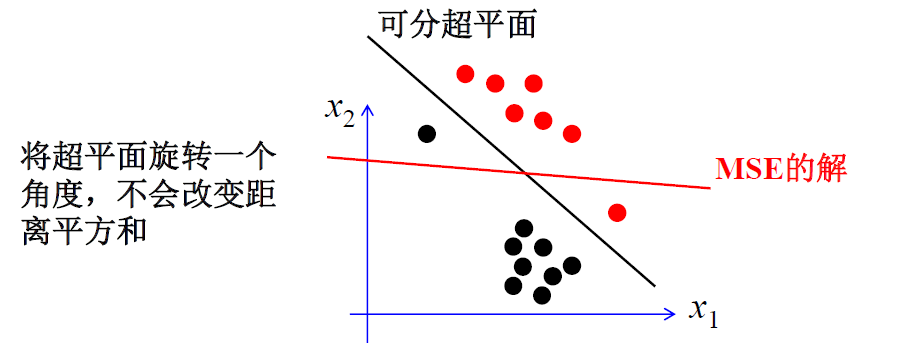
  如上图，MSE的解并不能实现线性可分样本集的正确分类

Ho-Kashyap方法

• MSE算法上最小化 $\Vert \mathbf{Ya}-\mathbf{b}{\Vert }^2$, 所得到的最优解并不需要位于可分超平面上
• 如果训练样本是线性可分的, 则可找到一个权向量 $\mathbf{a}$, 对所有样本, 均有 ${\mathbf{a}}^T{\mathbf{y}}_i>0$ 。换句话说, 一定存在一个 $\mathbf{a}$ 和 $\mathbf{b}$, 使$\mathbf{Ya}=\mathbf{b}>0$
• 但是, 事先并不知道 $\mathbf{b}$ 。因此, MSE准则函数可以更新为:$J_s(\mathbf{a},\mathbf{b})=\Vert \mathbf{Ya}-\mathbf{b}{\Vert }^2$
• 直接优化 $J_s(\mathbf{a},\mathbf{b})$ 将导致平凡解（都取 $0$ 直接就结束了）, 所以需要给 $\mathbf{b}$ 加一个 $\mathbf{b}>0$ 的约束条件。此时 $\mathbf{b}$ 可以解释为 margin
• 梯度
  $$\frac{\partial J_s(\mathbf{a},\mathbf{b})}{\partial \mathbf{a}}=2{\mathbf{Y}}^T(\mathbf{Ya}-\mathbf{b}),\frac{\partial J_s(\mathbf{a},\mathbf{b})}{\partial \mathbf{b}}=-2(\mathbf{Ya}-\mathbf{b})$$
• 对 $\mathbf{a}$ 而言, 总有 $\mathbf{a}={\mathbf{Y}}^{+}\mathbf{b}$, 其中 ${\mathbf{Y}}^{+}$为 $\mathbf{Y}$ 的伪逆${\left({\mathbf{Y}}^T\mathbf{Y}\right)}^{-1}{\mathbf{Y}}^T$
• 对 $\mathbf{b}$, 需要同时满足约束条件 $\mathbf{b}>0$ 。梯度更新:
  $${\mathbf{b}}_{k+1}={\mathbf{b}}_k-{\eta }_k\frac{\partial J_s(\mathbf{a},\mathbf{b})}{\partial \mathbf{b}}$$
• 由于 ${\mathbf{b}}_k$ 总是大于零, 要使 ${\mathbf{b}}_{k+1}$ 也大于零, 可以要求 $\partial J_s(\mathbf{a},\mathbf{b})/\partial \mathbf{b}$ 为负（若$\partial J_s(\mathbf{a},\mathbf{b})/\partial \mathbf{b}$ 为正，括号里面为$0$；若$\partial J_s(\mathbf{a},\mathbf{b})/\partial \mathbf{b}$ 为负，括号里面为负）
  $${\mathbf{b}}_1>0,{\mathbf{b}}_{k+1}={\mathbf{b}}_k-{\eta }_k\frac{1}{2}\left(\frac{\partial J_s(\mathbf{a},\mathbf{b})}{\partial \mathbf{b}}-\left|\frac{\partial J_s(\mathbf{a},\mathbf{b})}{\partial \mathbf{b}}\right|\right)$$
• $\frac{\partial J_s(\mathbf{a},\mathbf{b})}{\partial \mathbf{b}}=-2(\mathbf{Ya}-\mathbf{b})$，并记${\mathbf{e}}_k^{+}=\frac{1}{2}\left(\left(\mathbf{Y}{\mathbf{a}}_k-{\mathbf{b}}_k\right)+\left|\mathbf{Y}{\mathbf{a}}_k-{\mathbf{b}}_k\right|\right)$，则有
  $$\begin{array}{c}{\mathbf{a}}_k={\mathbf{Y}}^{+}{\mathbf{b}}_k\\ {\mathbf{b}}_1>0,{\mathbf{b}}_{k+1}={\mathbf{b}}_k+2{\eta }_k{\mathbf{e}}_k^{+}\end{array}$$
• 为了防止 $\mathbf{b}$ 收敛于 $0$, 可以让 $\mathbf{b}$ 从一个非负向量 $\left({\mathbf{b}}_1>0\right)$ 开始进行更新
• 由于要求 $\partial J_s(\mathbf{a},\mathbf{b})/\partial \mathbf{b}$ 等于 $0$, 在开始迭代时可令 $\partial J_s(\mathbf{a},\mathbf{b})/\partial \mathbf{b}$ 的元素为正的分量等于零, 从而加快收敛速度。
  
• 由于权向量序列 { a k } \left\{\mathbf{a}_k\right\} {ak​} 完全取决定于 { b k } \left\{\mathbf{b}_k\right\} {bk​}, 因此本质上讲 Ho-Kashyap 算法是一个生成margin 序列 { b k } \left\{\mathbf{b}_k\right\} {bk​} 的方法
• 由于初始 ${\mathbf{b}}_1>0$, 且更新因子 $\eta >0$, 因此 ${\mathbf{b}}_k$ 总是大于 $0$
• 对于更新因子 $0<\eta \le 1$, 如果问题线性可分, 则总能找到元素全为正的 $b$ （不懂）
• 如果 ${\mathbf{e}}_k=\mathbf{Y}{\mathbf{a}}_k-{\mathbf{b}}_k$ 全为 0 , 此时, ${\mathbf{b}}_k$ 将不再更新, 因此获得一个解。如果 ${\mathrm{e}}_k$ 有一部分元素小于 0 , 则可以证明该问题不是线性可分的 （不懂）