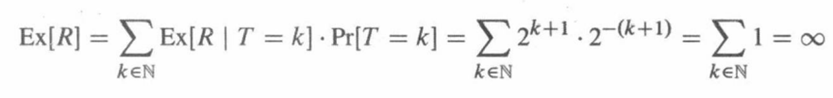有关卷绕+张力控制可以参看专栏的系列文章,文章链接如下:
变频器简单张力控制(线缆收放卷应用)_RXXW_Dor的博客-CSDN博客_收放卷应用张力控制的开闭环算法,可以查看专栏的其它文章,链接地址如下:PLC张力控制(开环闭环算法分析)_RXXW_Dor的博客-CSDN博客。https://blog.csdn.net/m0_46143730/article/details/127102822
1、卷径计算的常用6种方法
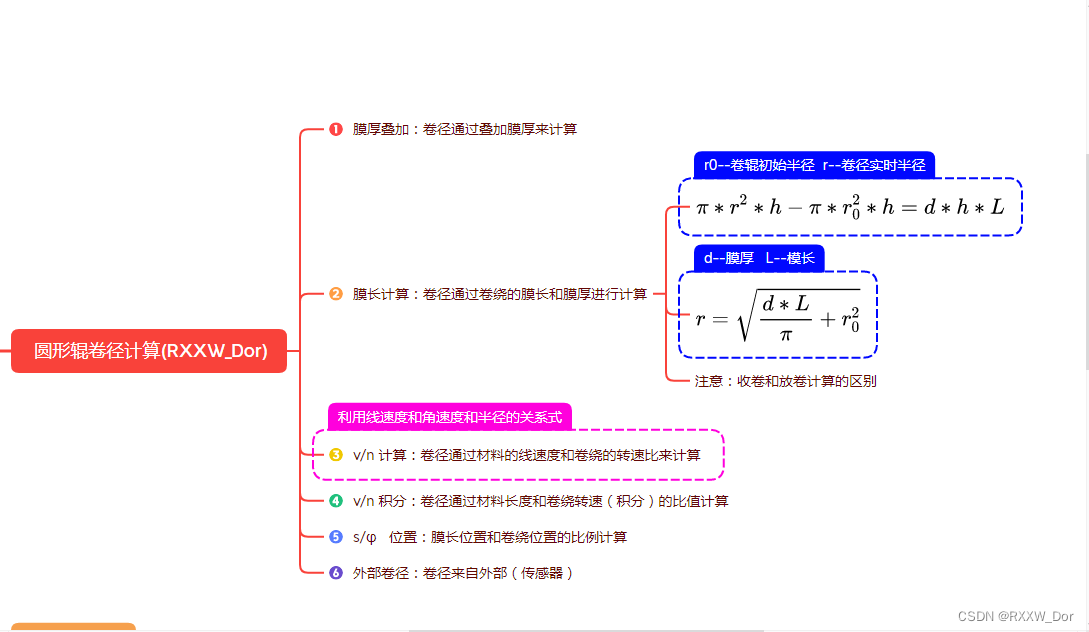
这里我们详细解读方法2,利用模长和膜厚计算卷径,膜厚通常属于规格参数,可以直接输入,模长我们可以利用计米器等外部编码器测量实时获得。