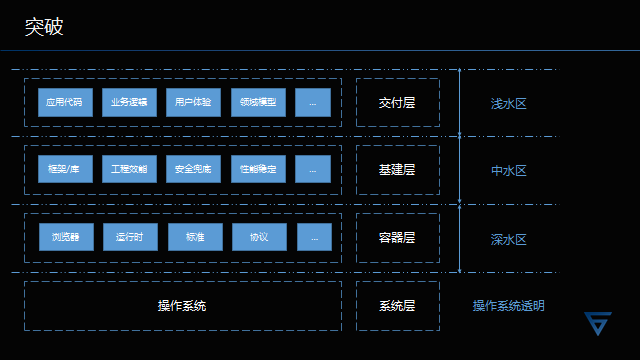
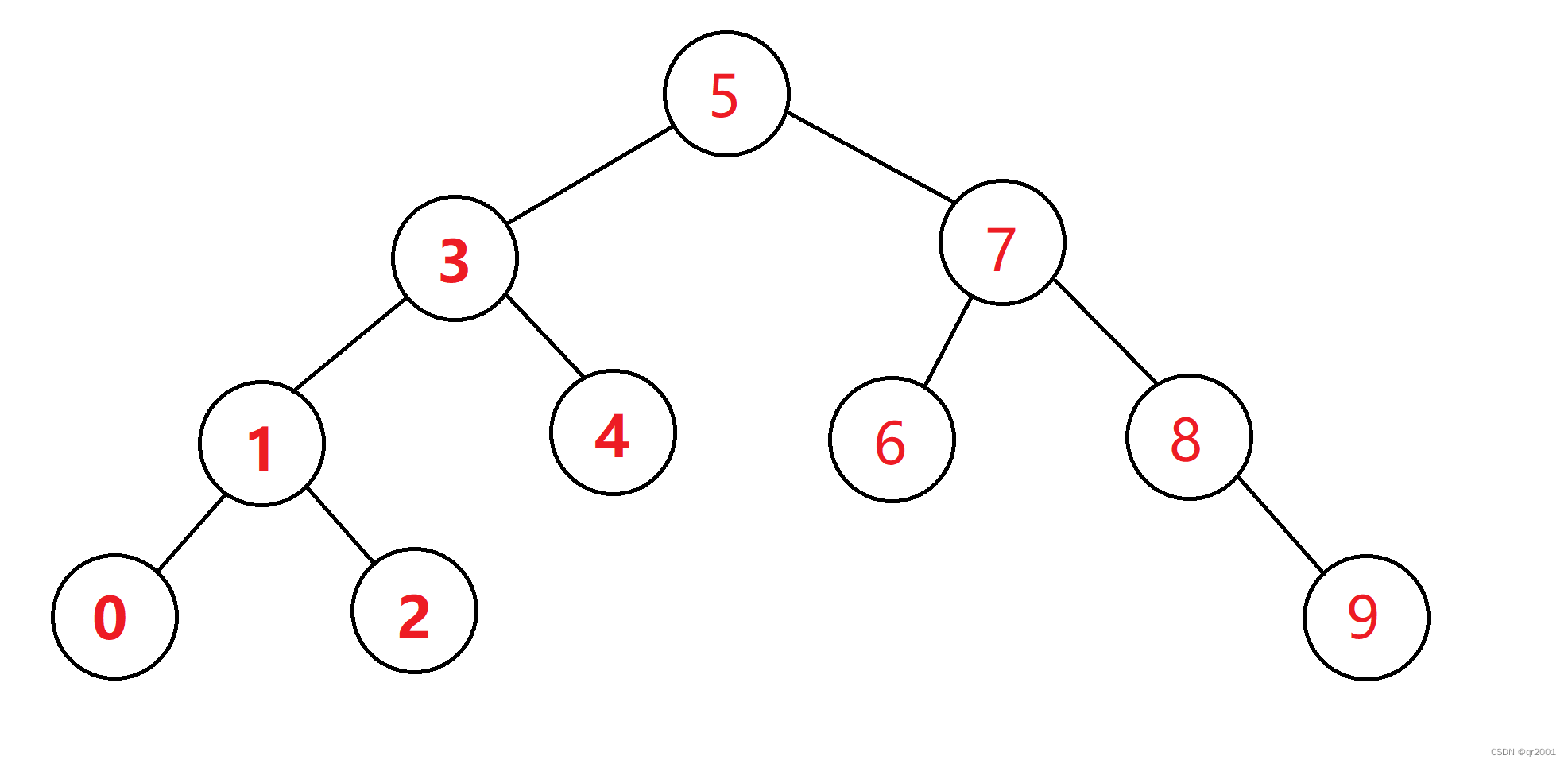
二叉搜索树

二叉树搜索树又叫二叉排序树，它还有可能为一个空树。搜索二叉树的性质有

若他的左子树不为空，则左子树上所有节点的值都小于根节点。
若他的右子树不为空，则右子树上所有节点的值都大于根节点。
他的左右子树均为二叉搜索树

迭代实现

template<class k>
struct BSTreeNode
{
	BSTreeNode<k>* _left;
	BSTreeNode<k>* _right;
	k _key;

	BSTreeNode(const k& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

template<class k>
struct BSTree
{
	typedef BSTreeNode<k> Node;
public:
	BSTree()
		:_root(nullptr)
	{}

	bool Insert(const k& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (parent->_key > key)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		return true;
	}

	bool Find(const k& key)
	{
		if (_root == nullptr)
		{
			return false;
		}
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

	bool Erase(const k& key)
	{
		Node* pertent = nullptr;
		Node* cur = _root;
	    //先找到要删除的
		while (cur)
		{
			if (cur->_key > key)
			{
				pertent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				pertent = cur;
				cur = cur->_right;
			}
			//找到了
			else
			{
				//开始删除
				//左为空，托孤右
				if (cur->_left == nullptr)
				{
					if (pertent == nullptr)
					{
						_root = cur->_right;
					}
					else
					{
						if (pertent->_left == cur)
						{
							pertent->left = cur->_right;
						}
						else
						{
							pertent->_right = cur->_right
						}
					}

					delete cur;
				}
				//右为空，托孤左
				else if (cur->_right == nullptr)
				{
					if (pertent == nullptr)
					{
						_root->_left;
					}
					else
					{
						if (pertent->_left == cur)
						{
							pertent->left = cur->_left;
						}
						else
						{
							pertent->_right = cur->_left;
						}
					}
					delete cur;
				}
				//左右均不为空，替换法删除
				else
				{
					//左子树的最右节点
					Node* minpertent = cur;
					Node* min = cur->_left;
					while (min->right)
					{
						minpertent = min;
						min = min->_right;
					}
					cur->_key = min->_key;//交换
					if (minpertent->_left == min)
					{
						minpertent->_left = min->_left;
					}
					else
					{
						minpertent->_right = min->_left;
					}
					delete min;
				}
			}
		}

		return false;
	}


	void Inorder()
	{
		_Inorder(_root);
	}
	void _Inorder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_Inorder(root->_left);
		cout << root->_key << " ";
		_Inorder(root->_right);
	}
private:
	Node* _root;
};

插入

要是插入key比这个根要大，那么就去根的右树，比根要小，那么就去左树。直到找到一个空位置。

查找

要是查找key比这个根要大，那么就去根的右树，比根要小，那么就去左树。直到找到，要是找不到就没有这个值。

删除

这里的删除才是最难的，在删除的时候我们可以大概分为三种方式

删除没有孩子的节点。
删除只有一个孩子的节点。
删除有两个孩子的节点。
对于第一第二种情况，我们可以采用直接删除法，要是没有孩子就直接释放掉要删的节点，要是有一个孩子我们直接将孩子托孤给该节点的父亲，再释放掉该节点。
对于有两个孩子的节点，我们采用替换法删除，就是将要删除的节点和左边最大右边最小的叶子节点进行替换之后然后删除叶子节点。

递归实现

template<class k>
struct BSTreeNode
{
	BSTreeNode<k>* _left;
	BSTreeNode<k>* _right;
	k _key;


	BSTreeNode(const k& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

template<class k>
struct BSTree
{
	typedef BSTreeNode<k> Node;
public:
	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}

	Node* FindR(const K& key)
	{
		return _FindR(_root, key);
	}

	Node* EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}
private:
	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}
		if (root->_key > key)
		{
			_InsertR(root->_left, key);
		}
		if (root->_key < key)
		{
			_InsertR(root->_right, key);
		}
		return false;
	}
	Node* _FindR(Node* root, const K& key)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		if (root->_key > key)
		{
			_FindR(root->_left, key);
		}
		else if (root->_key < key)
		{
			_FindR(root->_right, key);
		}
		else
		{
			return root;
		}
	}
	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			return false;
		}
		if (root->_key > key)
		{
			_EraseR(root->_left, key);
		}
		else if(root->_key < key)
		{
			_EraseR(root->_right, key);
		}
		else
		{
			Node* del = root;
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			else
			{
				Node* min = root->_right;
				while (min->_left)
				{
					min = min->_left;
				}

				swap(min->_key, root->_key);

				// 递归到右子树去删除
				_EraseR(root->_right, key);
			}
		}
		delete min;
		return true;
	}

private:
	Node* _root;
};