给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×1≤n,m≤1.5×
,
图中涉及边长均不小于 0,且不超过10000。
数据保证:如果最短路存在,则最短路的长度不超过 。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
堆优化版的dijkstra是对朴素版dijkstra进行了优化,在朴素版dijkstra中时间复杂度最高的寻找距离最短的点O(n^2)可以使用最小堆优化。
1. 一号点的距离初始化为零,其他点初始化成无穷大。
2. 将一号点放入堆中。
3. 不断循环,直到堆空。每一次循环中执行的操作为:
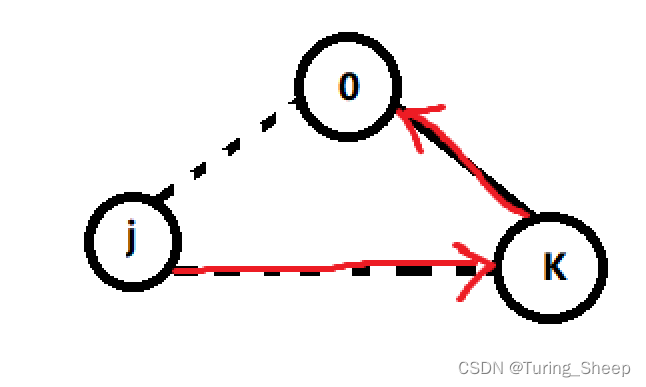
弹出堆顶,迭代每个点到邻接点的最短距离,从距离最小的点开始走
用该点更新临界点的距离,若更新成功就加入到堆中。
#include<stdio.h>
#include<iostream>
#include<math.h>
#include<algorithm>
#include<queue>
#include<string.h>
using namespace std;
typedef pair<int,int> PII;
const int N=1000100;
int h[N],e[N],ne[N],idx;
int w[N],dist[N];
bool st[N];
int n,m;
void add(int x,int y,int c)
{
w[idx]=c;
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
int dis()// 迭代每个点到邻接点的最短距离,从距离最小的点开始走(
{
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
priority_queue <PII , vector<PII> , greater<PII>>p;
p.push({0,1});
while(p.size())
{
PII k=p.top();
p.pop();
int dis=k.first , xu=k.second;
if(st[xu]) continue;
st[xu] = true;
for(int i = h[xu] ; i!=-1 ; i=ne[i])
{
int j=e[i];
if(dist[j]>dis+w[i])
{
dist[j]=dis+w[i];
p.push({dist[j],j});
}
}
}
if(dist[n]==0x3f3f3f3f) return -1;
else return dist[n];
}
int main()
{
memset(h,-1,sizeof(h));//初始化为-1
cin>>n>>m;
while(m--)
{
int x,y,c;
cin>>x>>y>>c;
add(x,y,c);
}
cout<<dis()<<endl;
return 0;
}