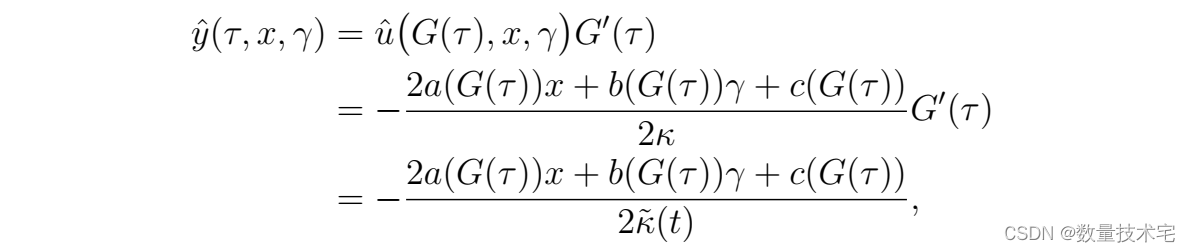模型
这里仅用一个简单的双积分模型
{
x
˙
i
=
v
i
v
˙
i
=
u
i
\begin{equation} \begin{cases} {\dot x}_i = v_i \\ {\dot v}_i = u_i \\ \end{cases} \end{equation}
{x˙i=viv˙i=ui
我们的控制最终的期望是使得状态趋于一致,即
lim
t
→
∞
∣
x
i
−
x
j
∣
=
0
lim
t
→
∞
∣
v
i
−
v
j
∣
=
0
\begin{aligned} \lim_{t \to \infty} |x_i - x_j| = 0 \\ \lim_{t \to \infty} |v_i - v_j| = 0 \\ \end{aligned}
t→∞lim∣xi−xj∣=0t→∞lim∣vi−vj∣=0
协议
这里我们用一个简单的控制协议
u
i
=
−
k
1
∑
j
=
1
N
(
x
i
−
x
j
)
−
k
2
∑
j
=
1
N
(
v
i
−
v
j
)
u_i = -k_1 \sum_{j=1}^N (x_i - x_j) - k_2 \sum_{j=1}^N (v_i - v_j)
ui=−k1j=1∑N(xi−xj)−k2j=1∑N(vi−vj)
代码
clear;
close all;
clc;
% 拉普拉斯矩阵作为全局变量
global L;
% 图论
A=[0 1 0 0 1;
1 0 1 0 0;
0 1 0 1 0;
0 0 1 0 1;
1 0 0 1 0];
D=diag(sum(A,2));
L=D-A;
% 初始化
X0=[0;-1;2;1.5;1.2];
V0=[0;1;2;-1.5;-2];
% 迭代
options = odeset('MaxStep', 1e-2, 'RelTol',1e-2,'AbsTol',1e-4);
[t,y] = ode45(@odefun,[0 15],[X0;V0],options);
X = y(:,1:5);
V = y(:,6:10);
U_save=[];
% 重现控制量U
for i = 1:length(t)
eX = L*y(i,1:5)';
eV = L*y(i,6:10)';
eu = controlInput(eX, eV);
U_save = [U_save;eu'];
end
%% 画图部分
fig1 = figure(1);
plot(t,X);
xlabel('t(sec)');
ylabel('position');
fig2 = figure(2);
plot(t,V);
xlabel('t(sec)');
ylabel('velocity');
fig3 = figure(3);
plot(t,U_save);
xlabel('t(sec)');
ylabel('u');
print(fig1, './fig1.png', '-dpng', '-r300');
print(fig2, './fig2.png', '-dpng', '-r300');
print(fig3, './fig3.png', '-dpng', '-r300');
%% 函数部分
function dydt = odefun(t,y)
global L;
dydt = zeros(10,1);
eX = L*y(1:5);
eV = L*y(6:10);
U = controlInput(eX,eV);
dydt(1:5)=y(6:10);
dydt(6:10)=U;
end
%% 计算输入
function u = controlInput(eX, eV)
k1 = 1;
k2 = 1;
u = - k1 .* eX - k2 .* eV;
end
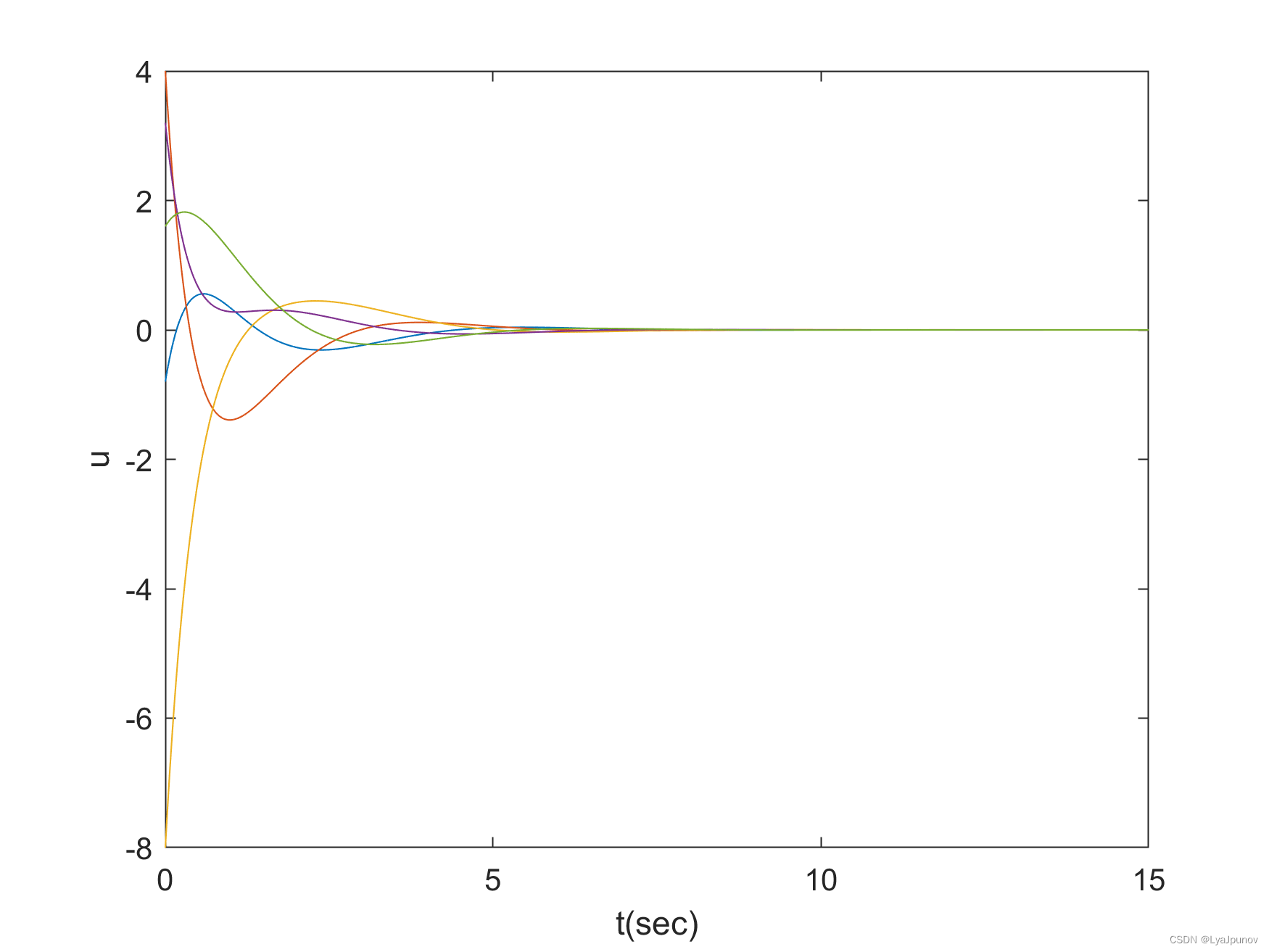
仿真
位置
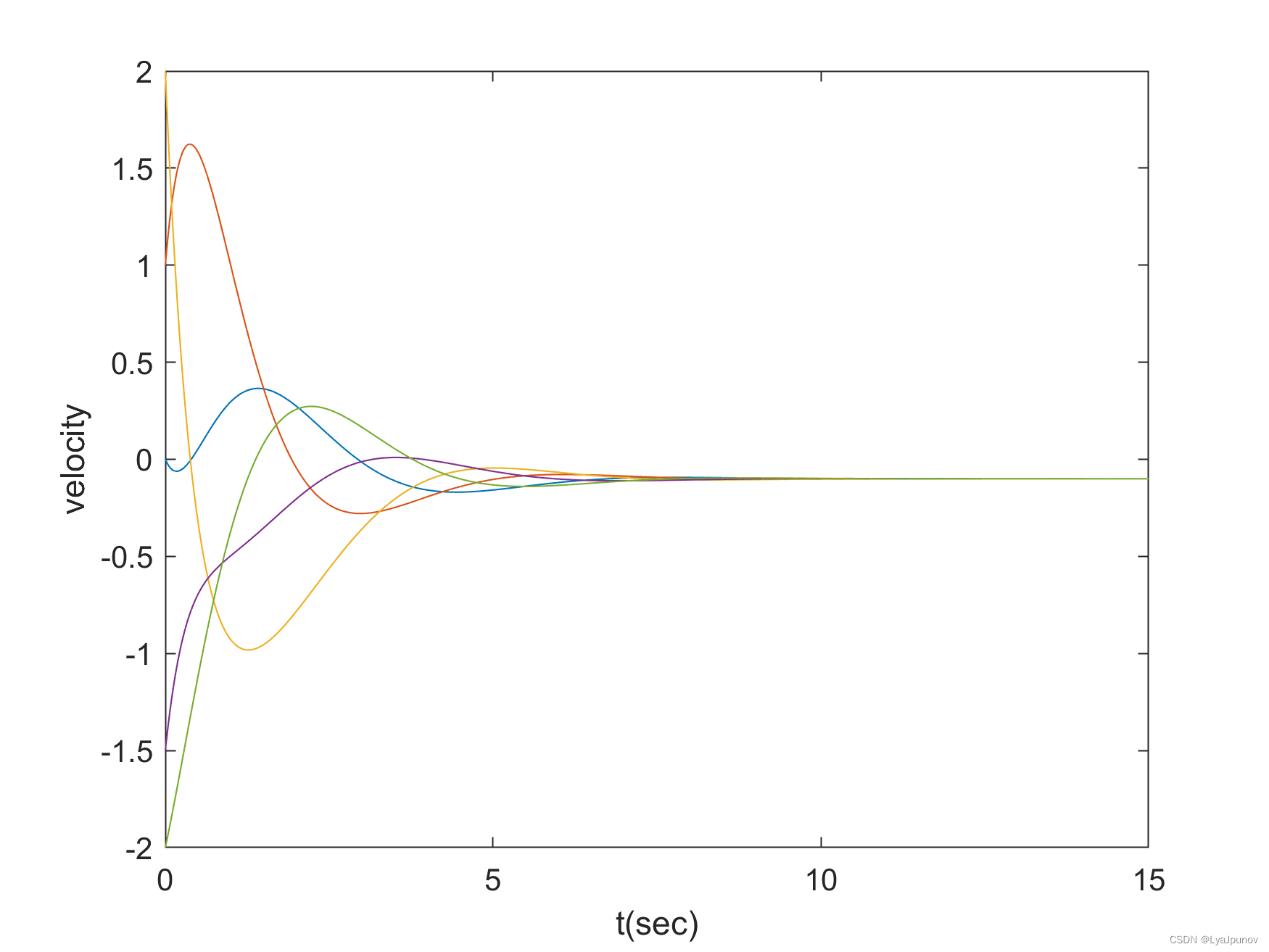
速度
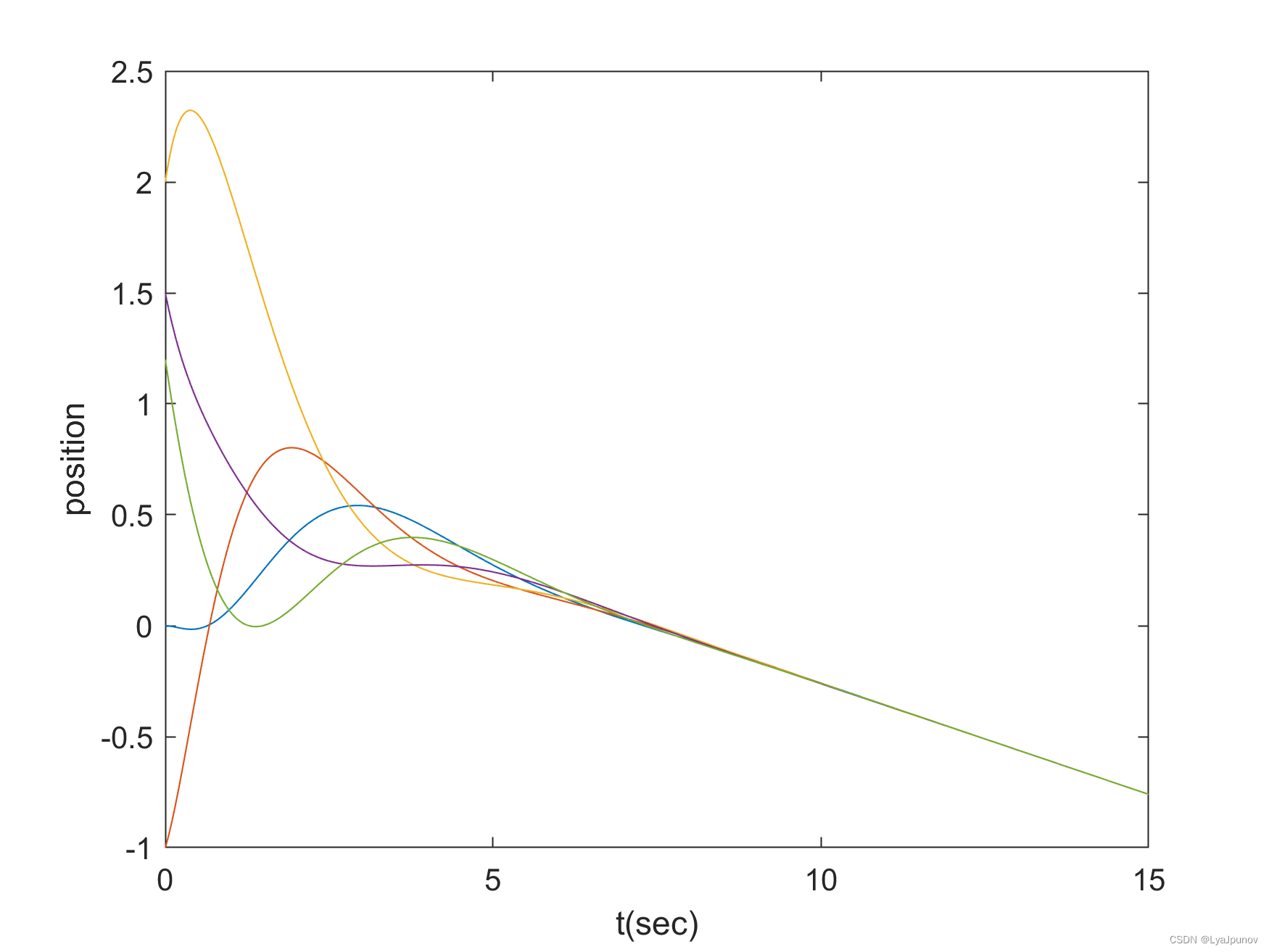
控制量