1.欧式距离(Euclidean Distance)
欧式距离源自N维欧氏空间中两点间的距离公式:
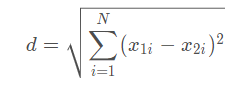
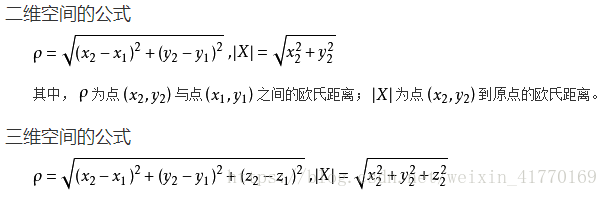
代码实践
from scipy import spatial
vec1 = [1, 2, 3, 4]
vec2 = [5, 6, 7, 8]
euclidean = spatial.distance.euclidean(vec1, vec2)
print(euclidean)
2.标准化欧式距离(Standardized Euclidean distance)
引入标准化欧式距离的原因是一个数据的各个维度之间的尺度不一样。
【对于尺度无关的解释】如果向量中第一维元素的数量级是100,第二维的数量级是10,比如v1=(100,10),v2 = (500,40),则计算欧式距离
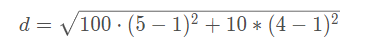
可见欧式距离会给与第一维度100权重,这会压制第二维度的影响力。对所有维度分别进行处理,使得各个维度的数据分别满足标准正态分布: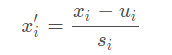
是 该维度所有数据的均值,
是对应方差。
然后在对进行欧式距离:
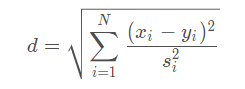
代码实践
from scipy import spatial
vec1 = [1, 2, 3, 4]
vec2 = [5, 6, 7, 8]
w = [0.1, 0.1, 0.2, 1]
seuclidean = spatial.distance.seuclidean(vec1, vec2, w)
print(seuclidean)3. 马氏距离(Mahalanobis Distance)
马氏距离又称为数据的协方差距离,它是一种有效的计算两个未知样本集的相似度的方法。马氏距离的结果也是将数据投影到N(0,1)区间并求其欧式距离,与标准化欧氏距离不同的是它认为各个维度之间不是独立分布的,所以马氏距离考虑到各种特性之间的联系。
马氏距离可以通过协方差自动生成相应的权重,而使用逆则抵消掉这些权重。
最典型的就是根据距离作判别问题,即假设有n个总体,计算某个样品X归属于哪一类的问题。此时虽然样品X离某个总体的欧氏距离最近,但是未必归属它,比如该总体的方差很小,说明需要非常近才能归为该类。对于这种情况,马氏距离比欧氏距离更适合作判别。
代码实践
from scipy.spatial import distance
iv = [[1, 0.5, 0.5], [0.5, 1, 0.5], [0.5, 0.5, 1]]
print (distance.mahalanobis([1, 0, 0], [0, 1, 0], iv))4.余弦距离(余弦相似性)cosine similarity
定义:
余弦相似度(Cosine Similarity)是n维空间中两个n维向量之间角度的余弦。它等于两个向量的点积(向量积)除以两个向量长度(或大小)的乘积。
公式:
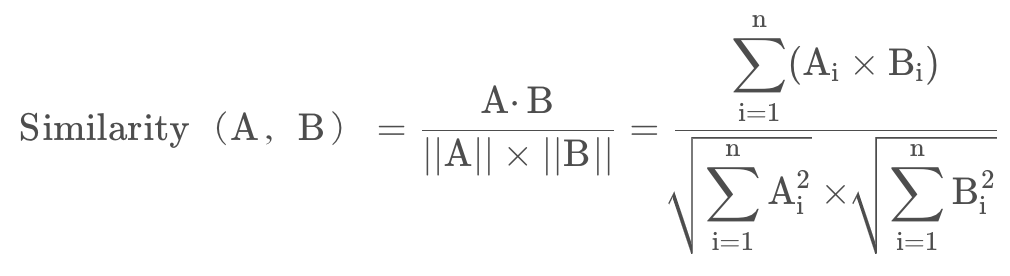
值的范围为[-1,1],-1为完全不相似,1为完全相似。
在向量表示的三角形中,假设a向量是(x1, y1),b向量是(x2, y2),那么可以将余弦定理改写成下面的形式:
例子:
句子A:这只皮靴号码大了。那只号码合适
句子B:这只皮靴号码不小,那只更合适
怎样计算上面两句话的相似程度?
基本思路是:如果这两句话的用词越相似,它们的内容就应该越相似。因此,可以从词频入手,计算它们的相似程度。
第一步,分词。
句子A:这只/皮靴/号码/大了。那只/号码/合适。
句子B:这只/皮靴/号码/不/小,那只/更/合适。
第二步,列出所有的词。
这只,皮靴,号码,大了。那只,合适,不,小,很
第三步,计算词频。
句子A:这只1,皮靴1,号码2,大了1。那只1,合适1,不0,小0,更0
句子B:这只1,皮靴1,号码1,大了0。那只1,合适1,不1,小1,更1
第四步,写出词频向量。
句子A:(1,1,2,1,1,1,0,0,0)
句子B:(1,1,1,0,1,1,1,1,1)
到这里,问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段,都是从原点([0, 0, …])出发,指向不同的方向。
两条线段之间形成一个夹角,
如果夹角为0度,意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等;
如果夹角为90度,意味着形成直角,方向完全不相似;
如果夹角为180度,意味着方向正好相反。
因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
计算结果如下:
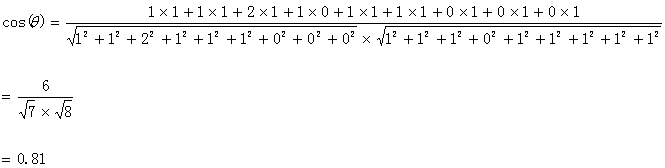
计算结果中夹角的余弦值为0.81非常接近于1,所以,上面的句子A和句子B是基本相似的
由此,我们就得到了文本相似度计算的处理流程是:
(1)找出两篇文章的关键词;
(2)每篇文章各取出若干个关键词,合并成一个集合,计算每篇文章对于这个集合中的词的词频
(3)生成两篇文章各自的词频向量;
(4)计算两个向量的余弦相似度,值越大就表示越相似。
优点:余弦距离根据向量方向来判断向量相似度,与向量各个维度的相对大小有关,不受各个维度直接数值影响。
某种程度上,归一化后的欧氏距离和余弦相似性表征能力相同。
代码实践
1. 在Python中使用scipy计算余弦相似性
scipy 模块中的spatial.distance.cosine() 函数可以用来计算余弦相似性,但是必须要用1减去函数值得到的才是余弦相似度。
from scipy import spatial
vec1 = [1, 2, 3, 4]
vec2 = [5, 6, 7, 8]
cos_sim = 1 - spatial.distance.cosine(vec1, vec2)
print(cos_sim)2. 在Python中使用numpy计算余弦相似性
numpy模块没有直接提供计算余弦相似性的函数,我们可以根据余弦相似性的计算公式来计算。其中numpy.doy()函数可以计算两个向量的内积,numpy.linalg.norm()函数返回向量的模。
import numpy as np
vec1 = np.array([1, 2, 3, 4])
vec2 = np.array([5, 6, 7, 8])
cos_sim = vec1.dot(vec2) / np.linalg.norm(vec1) * np.linalg.norm(vec2)
print(cos_sim)注意numpy只能计算numpy.ndarray类型向量的余弦相似性。
3. 在Python中使用sklearn计算余弦相似性
sklearn提供内置函数cosine_similarity()可以直接用来计算余弦相似性。
import numpy as np
from sklearn.metric.pairwise import cosine_similarity()
vec1 = np.array([1, 2, 3, 4])
vec2 = np.array([5, 6, 7, 8])
cos_sim = cosine_similarity(vec1.reshape(1, -1), vec2.reshape(1, -1))
print(cos_sim[0][0])4. 在Python中使用torch计算余弦相似性
torch模块提供cosine_similarity()函数用于计算张量的余弦相似性
import torch
import torch.nn.functional as F
vec1 = torch.FloatTensor([1, 2, 3, 4])
vec2 = torch.FloatTensor([5, 6, 7, 8])
cos_sim = F.cosine_similarity(vec1, vec2, dim=0)
print(cos_sim) 注意,cosine_similarity()函数只能对torch.Tensor类型的张量进行计算,计算结果返回的仍然是一个torch.Tensor类型的数据。
5.汉明距离(Hammi)
汉明距离是两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。比如:
1011101 与 1001001 为 2
2143896 与 2233796 是 3
可以把它看做将一个字符串变换成另外一个字符串所需要替换的字符个数。
此外,汉明重量是字符串相对于同样长度的零字符串的汉明距离,如:
11101 的汉明重量是 4。
所以两者间的汉明距离等于它们汉明重量的差a-b
代码实践
from scipy import spatial
vec1 = [1, 2, 3, 4]
vec2 = [5, 6, 7, 8]
hamming_distance = spatial.distance.hamming(vec1, vec2)
print(hamming_distance)6.曼哈顿距离 (Manhattan distance)
曼哈顿距离的定义如下: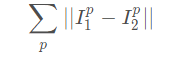
p是I的维度。当I为图像坐标时,曼哈顿距离即是x,y坐标距离之和。