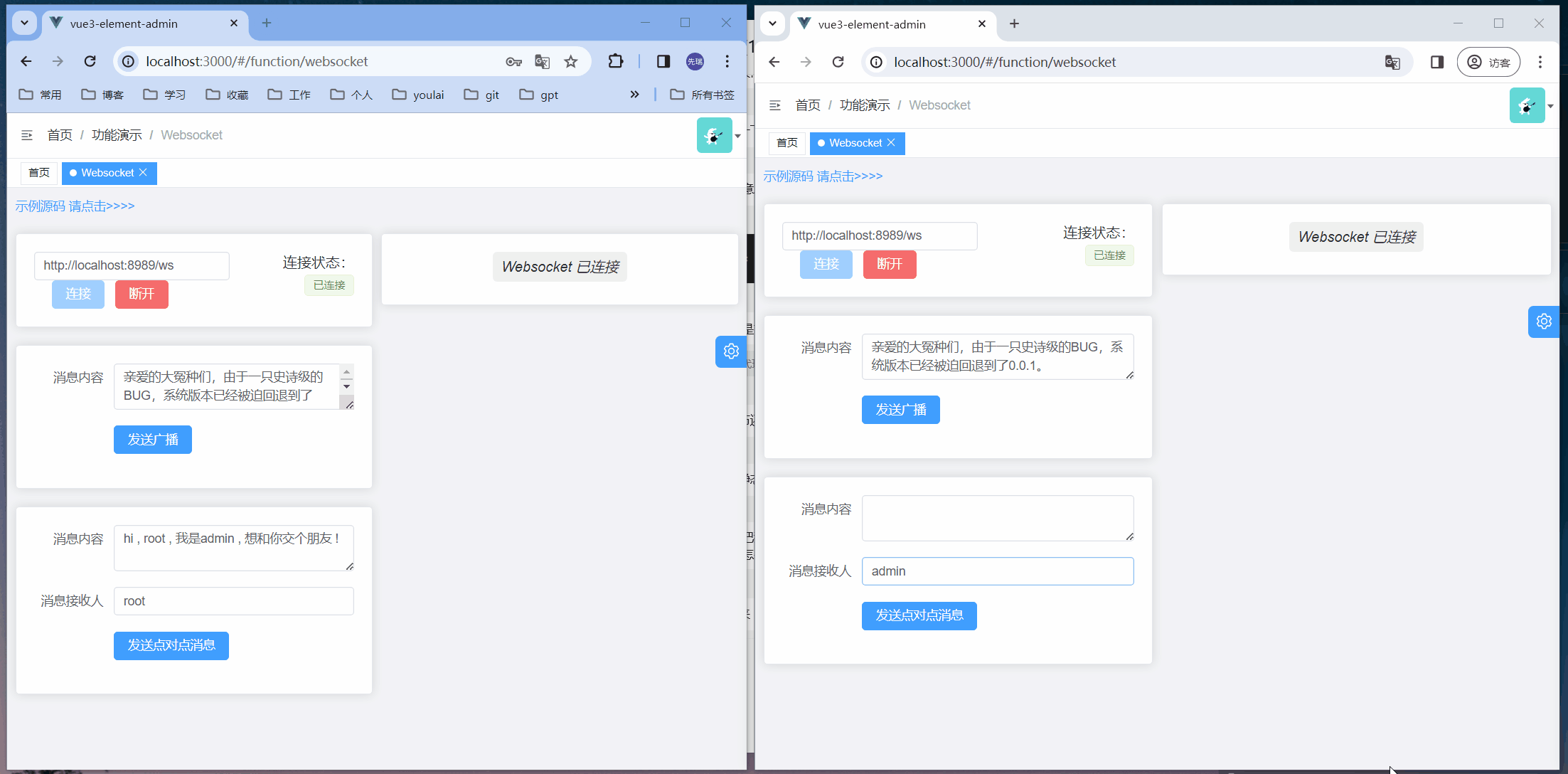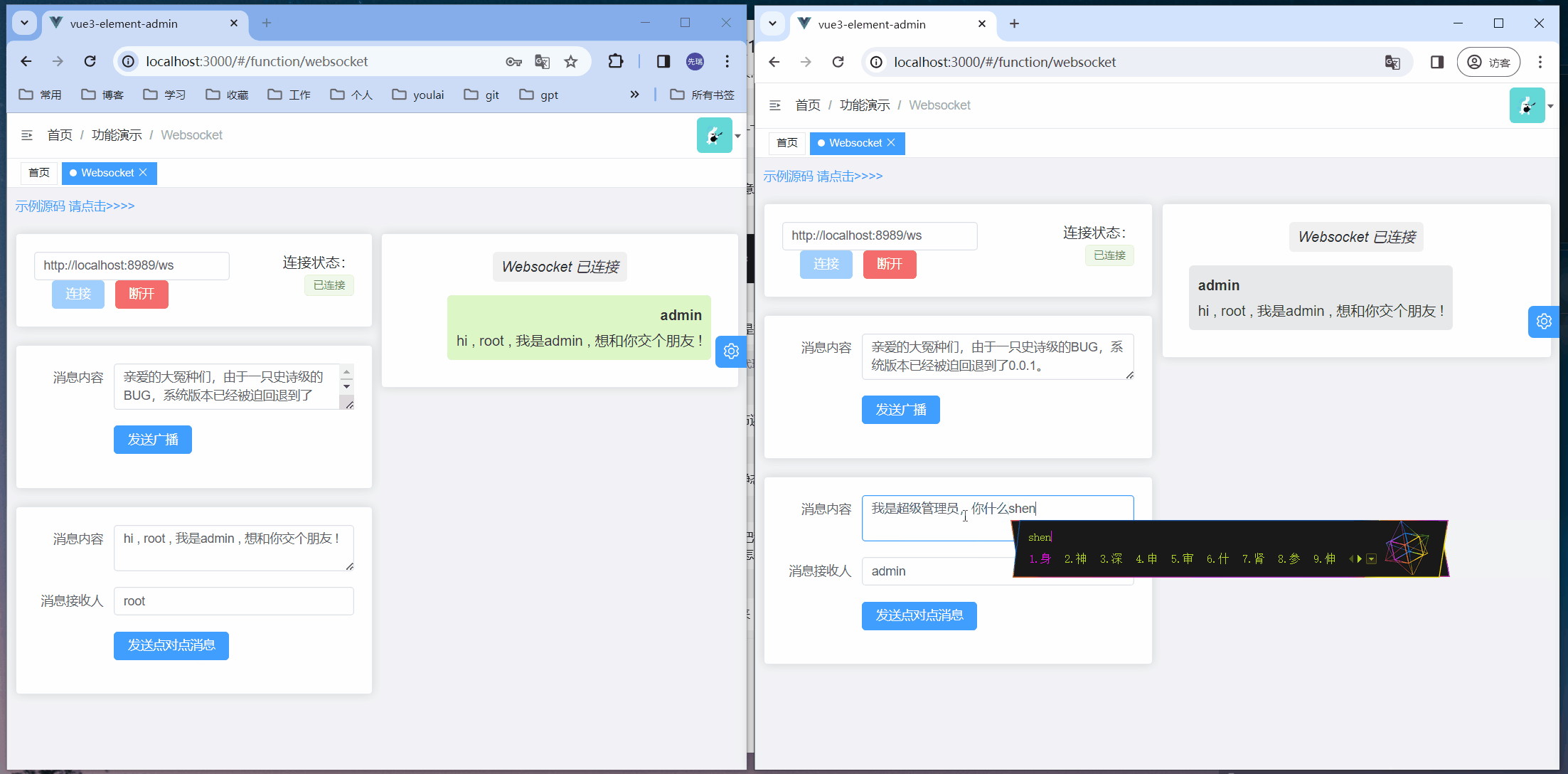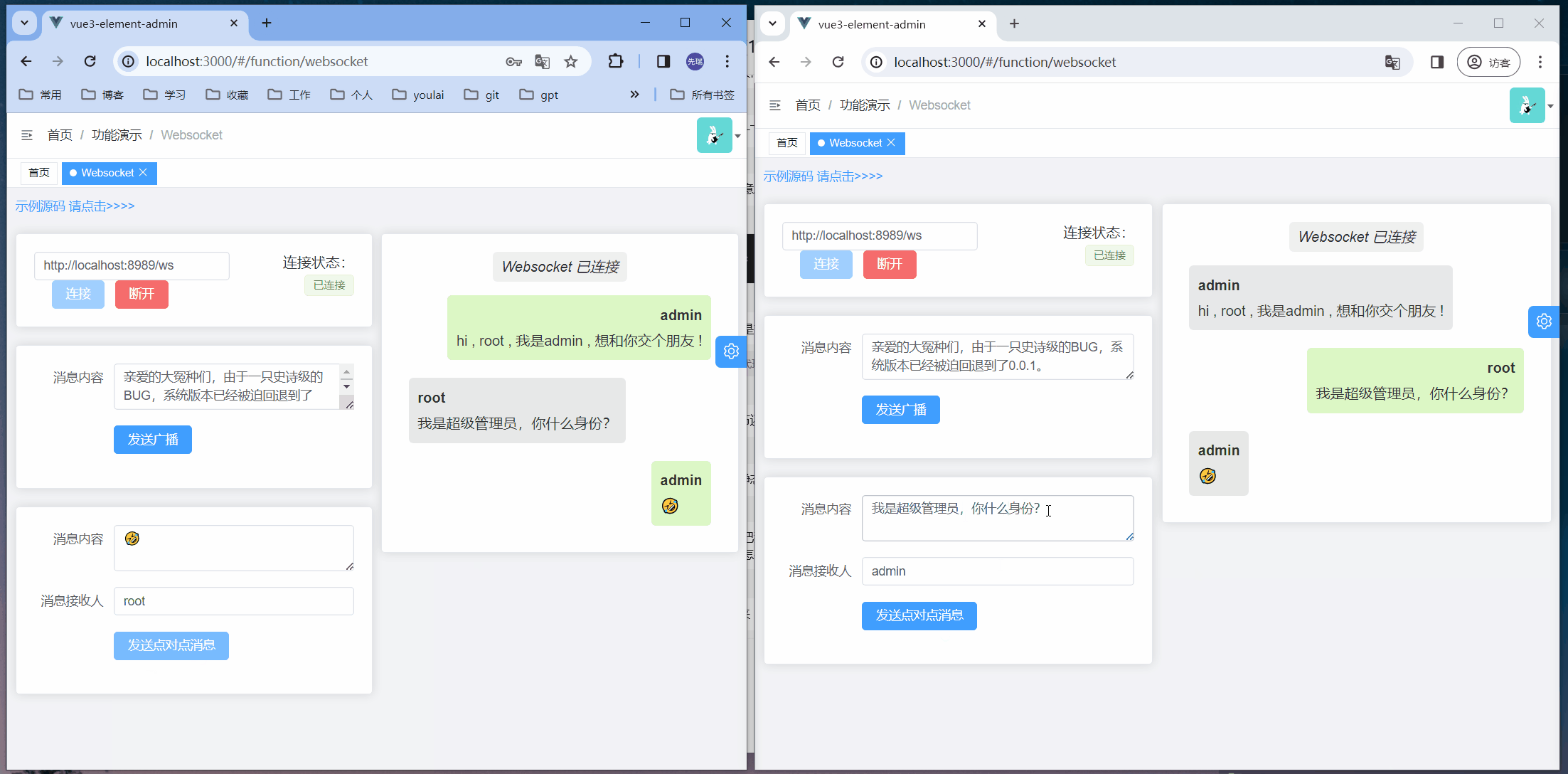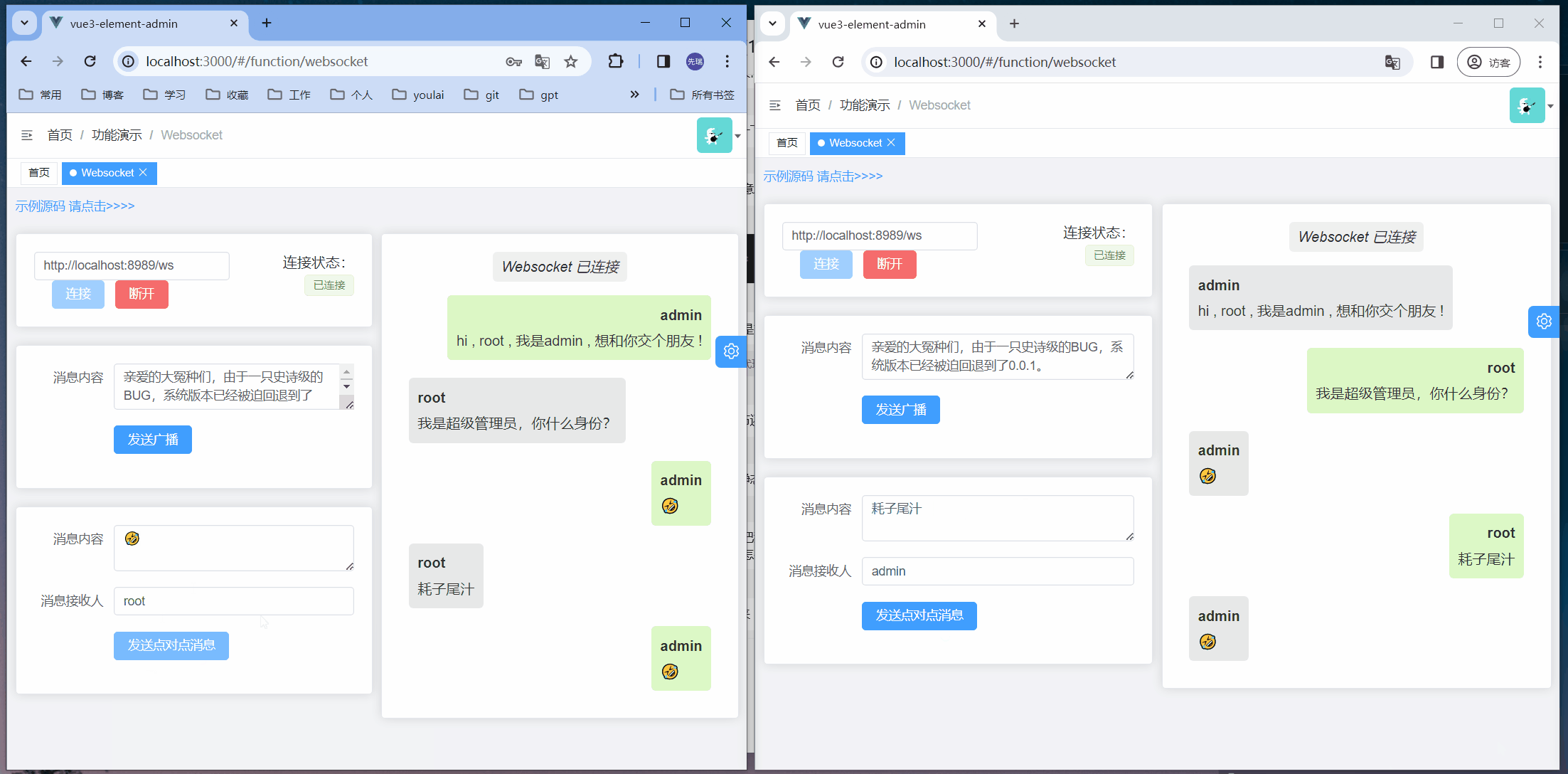
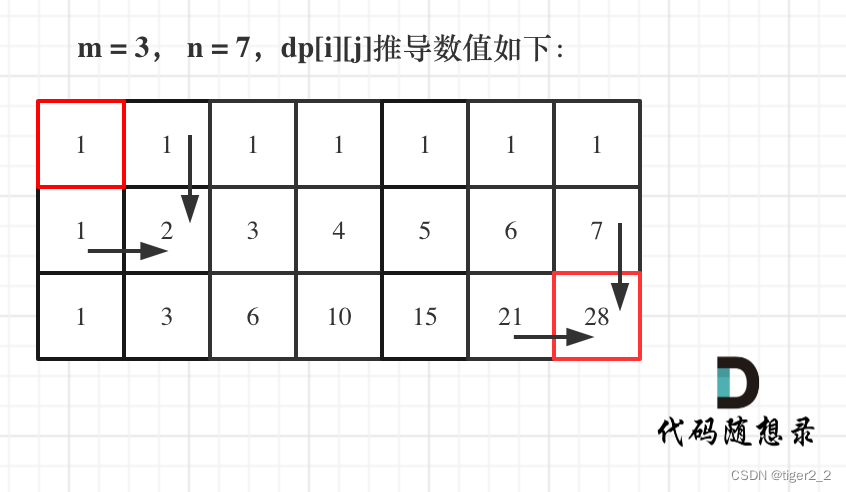
62.不同路径
每次向右或者向下走两个选择,定义dp数组dp[i][j] 为到达索引ij的路径和,状态转移公式为
dp[i][j]=dp[i-1][j]+dp[i][j-1],初始状态的第一行和第一列为1,从左上到右下开始遍历即可。详细代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>>dp (m,vector<int>(n,1));
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};为了优化空间复杂度,可以用一个一维数组,因为一定是先更新左边的值再更新右边的值。
详细代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int>dp (n,1);
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[j]+=dp[j-1]; //当前dp为从上方路径来,dp[j-1]为从左方来
}
}
return dp[n-1];
}
};63. 不同路径 II
这道题和上一道思路一样,但是这道有障碍物,需要注意有障碍物的索引,到达该处的路径和为0,根据这个条件,增加处理逻辑即可,整体的转移方程还是
详细代码如下:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty()) return 0;
vector<vector<int>>dp(obstacleGrid.size(),vector<int>(obstacleGrid[0].size(),0));
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
for(int i=0;i<m;i++)
{
if(obstacleGrid[i][0]==1||i>0&&dp[i-1][0]==0) dp[i][0]=0;
else dp[i][0] = 1;
}
for(int j=1;j<n;j++)
{
if(obstacleGrid[0][j]==1||dp[0][j-1]==0) dp[0][j]=0;
else dp[0][j] = 1;
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
if(obstacleGrid[i][j]==1) dp[i][j]=0;
else dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};感觉这道题的优化空间版本细节有点多,但还是附上代码:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty()) return 0;
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<int>dp (n,0);
for(int j=0;j<n;j++)
{
if(obstacleGrid[0][j]==1||j>0&&dp[j-1]==0) dp[j]=0;
else dp[j] = 1;
}
for(int i=1;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(obstacleGrid[i][j]==1) dp[j]=0;
else if(j>0) dp[j] = dp[j]+dp[j-1];
}
}
return dp[n-1];
}
};