置信区间是统计学中的一个重要工具，是用样本参数()估计出来的总体均值在某置信水平下的范围。通俗一点讲，如果置信度为95%（等价于显著水平a=0.05），置信区间为[a,b]，这就意味着总体均值落入该区间的概率为95%，或者以95%的可信程度相信总体均值在这个范围内。

一般情况下当我们抽样的数量大于等于30时，可认为样本均值服从正态分布，以此我们通过查标准正态分布表，获得显著水平a下的z值，用以下公式即可获得置信区间。

 如果样本数量小于30，我们可以根据中心极限定理，进行多轮抽样产生均值样本，计算置信区间。如下例所示。

工厂要确定95%置信水平下的产品成份含量的置信区间，但手里只有20个样本数据，如何来估计总体的成分含量呢？

我们可以对这20个样本数据进行30轮重复采样，每次随机采样10件产品，记录其均值。这样会得到由30个均值构成的样本。根据中心极限定理，这个样本服从正态分布，于是我们就可以用这个均值样本来估计总体的成分含量置信区间了。

 示例代码如下：

#初始化样本
X=np.array([91,94,91,94,97,83,91,95,94,96,97,95,90,91,95,91,88,85,89,93])

#样本排序，为了适应下面的随机抽样函数
X=sorted(X)

#使用random模块的随机抽样函数sample，进行抽样。该函数有两个参数，第一个是样本集合，第二个是抽取数量
import random

#进行30轮随机抽样同时计算均值，形成新的正态分布的样本
n=30
X_new=[np.mean(random.sample(X, 10)) for i in range(n)]

#计算样本均值和标准差
mu,std=np.mean(X_new),np.std(X_new)

#求置信区间
[mu-std/np.sqrt(n)*1.96,mu+std/np.sqrt(n)*1.96]

最终估计的总体均值置信区间为[91.69, 92.18]。

---

中心极限定理：无论样本所属总体服务什么分布，对该样本进行n次随机采样，产生n个新的样本，那么这n个样本的n个均值所在总体服务正态分布。而且n越大，越接近正态分布。如下例

这是0到9，10个数构成的样本，其分布图如下所示，是一个均匀分布。

然后我们进行20轮重复采样，每次采集2个数字，形成的均值样本分布如下图所示， 正态分布还不明显

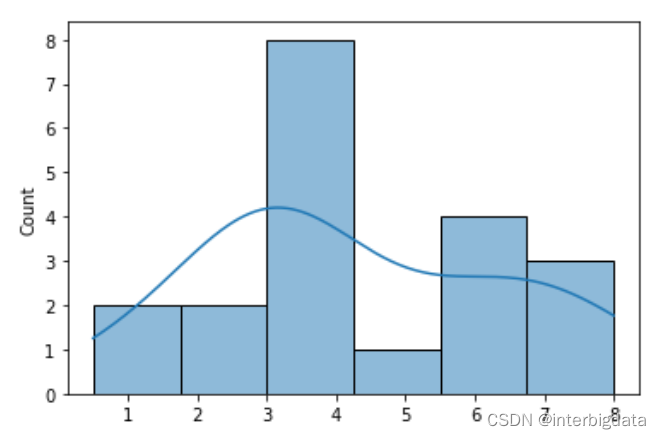
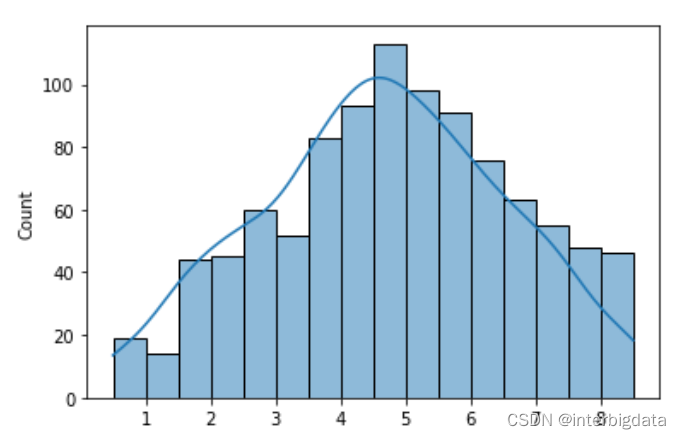
 进行50轮重复采样，形成的均值样本分布如下图所示， 正态分布开始显现

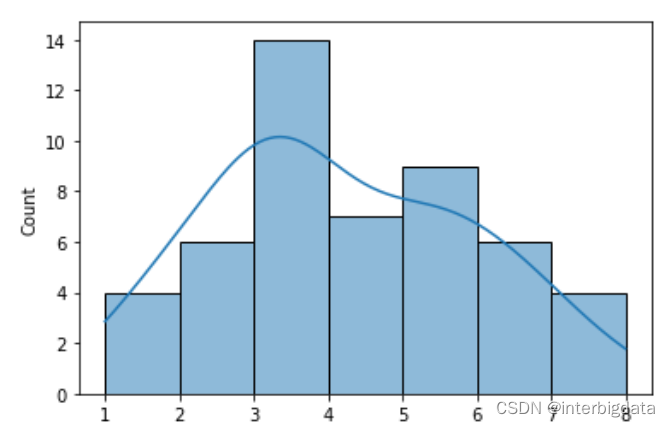
进行1000轮重复采样，形成的均值样本分布如下图所示， 基本呈正态分布