404 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。
示例 1：

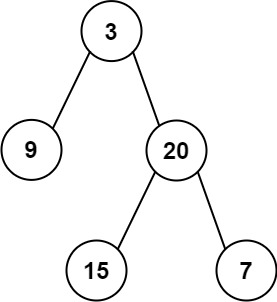
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

思路

迭代法

迭代法理解起来更容易，就是遍历每一个结点，去获取左叶子结点的值，然后加起来

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 法一: 迭代法 遍历每一个结点 采用中左右的方式
class Solution(object):
    def sumOfLeftLeaves(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        sum = 0 # 最终结果
        stack = [root] # 存储遍历结果
        while stack:
            node = stack.pop() # 弹出
            if node.left and (not node.left.left) and (not node.left.right): # 注意判断是否是叶子结点的方式
                sum += node.left.val
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        return sum

递归法

递归法也需要掌握
递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲：

1. 确定递归函数的参数和返回值

判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int
使用题目中给出的函数就可以了。

2. 确定终止条件

如果遍历到空节点，那么左叶子值一定是0

if not root:
    return 0

注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：

if not root.left and not root.right:
    return 0 # 这个判断条件也可以不用写

3. 确定单层递归的逻辑

当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。（单层逻辑 严格按照左中右的顺序）

# 左
left_sum = self.sumOfLeftLeaves(root.left)
if root.left and (not root.left.left) and (not root.left.right):
    left_sum = root.left.val
# 右
right_sum = self.sumOfLeftLeaves(root.right)
sum = left_sum + right_sum # 中

整体递归代码：

# 法二: 递归法 遍历方式：左右中
class Solution(object):
    def sumOfLeftLeaves(self, root):
        if not root:
            return 0
        # 左
        left_sum = self.sumOfLeftLeaves(root.left)
        if root.left and (not root.left.left) and (not root.left.right):
            left_sum = root.left.val
        # 右
        right_sum = self.sumOfLeftLeaves(root.right)
        sum = left_sum + right_sum # 中
        return sum