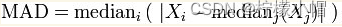信号与线性系统预备训练3——MATLAB软件在信号与系统中的应用初步

news2024/11/30 1:37:47

信号与线性系统预备训练3——MATLAB软件在信号与系统中的应用初步

The Preparatory training3 of Signals and Linear Systems

对应教材：《信号与线性系统分析（第五版）》高等教育出版社，吴大正著

一、目的

1.熟悉和回顾MATLAB软件的基本操作和编程，为本课程翻转课堂和实验中基于MATLAB进行信号和系统的分析做好准备。
2.基于MATLAB，熟悉和回顾本课程所需的一些数学基础知识

二、任务安排及要求

1.根据所给出的各项内容要求，每位同学自主独立完成相关资料查阅、知识回顾和基于MATLAB的软件设计和调试，汇总分析相关结果并撰写报告（报告主要用于在课堂上做汇报展示，可以采用Word或者PPT形式，具体格式不限）。在完成任务的过程中，可以与其他同学商讨，或者向老师咨询，但应独立完成报告。
2.课堂上将随机抽取部分同学上台汇报展示（每位同学只展示其中部分内容），教师和其他同学针对该同学的汇报展示进行提问和讨论（教师提问有可能针对台下其他同学）。
3.熟练掌握MATLAB的基本操作和程序设计。

三、具体步骤要求

1、脚本与函数

要求：

（1）了解MATLAB的脚本和函数的概念，总结其联系和区别。举例说明对脚本文件和函数文件的命名有什么要求？
（2）任意编写一个MATLAB函数（函数功能自定），并利用脚本文件调用该函数，实现相应的函数功能。据此总结MATLAB函数的调用原理和方法。

解答：

（1）
联系：
脚本文件和函数文件都是m文件。
脚本是可以独立运行的，函数不能独立运行，需要被调用。
（2）
函数

%b、a分别为直接型的分子和分母系数
%C、B、A分别为并联型的常数项，分子项矩阵，分母项矩阵
function [C,B,A]=tf2par(b,a)
[r,p,C]=residuez(b,a);
N=length(r);            
A=zeros(ceil(N/2),3);
B=A;                    
k=1;                   
if mod(N,2)==1          
for i=1:2:N-1
[B(k,:),A(k,:)]=residuez([r(i),r(i+1)],[p(i),p(i+1)],0);
k=k+1;
end
B(end,:)=[r(end),0,0];
A(end,:)=[1,-p(end),0];
else                    
for i=1:2:N
[B(k,:),A(k,:)]=residuez([r(i),r(i+1)],[p(i),p(i+1)],0);
k=k+1;
end
end
end

调用

syms z;
A=[1 2 -3 4 5 -6 7];
B=[7 -6 5 4 -3 2 1];
[S,G]=tf2sos(B,A)
[c,b,a]=tf2par(B,A)

调用格式：
[输出参数1，输出参数2，…]=函数名（输入参数1，输入参数2，…）
函数调用可以嵌套，一个函数可以调用别的函数，甚至调用它自己。

2、符号运算和数值运算

要求：

符号运算和数值运算是MATLAB中两种不同的数学运算模式，其用途也不同。符号运算一般用于理论推导，得到的是运算结果的解析表达式；数字运算一般用于数值求解和图形化展示，得到的运算结果是数据（数组、矩阵），可以直接绘制成图表的形式。
（1）进一步了解符号运算与数值运算的区别，掌握两种不同运算模式的基本编程方法。
（2）了解符号运算函数dsolve（求解微分方程）、fourier（傅里叶变换）、ifourier（傅里叶反变换）、laplace（拉普拉斯变换）、ilaplace（拉普拉斯反变换）、ztrans（Z变换）、iztrans（Z反变换）等的功能，分别举例说明这些函数的用法。
（3）根据傅里叶变换的定义，采用数值运算的方法计算某个函数（具体函数自定）的傅里叶变换。若自己独立编程完成有困难，可以咨询老师或者到网络上搜索相关示例，但应该理解其运算原理和程序设计原理。

解答：

（1）
创建符号变量的基本方法——利用syms命令
例如：

syms x a b
f=x^2+a*x+b;
fx=diff(f,x)

运行结果：

fx = a + 2*x

数值运算为直接赋值
例如：

a=1;
b=2;
c=a+b

运行结果：

c = 3

（2）
dsolve：用来解符号常微分方程、方程组，如果没有初始条件，则求出通解，如果有初始条件，则求出特解。
句法：

S = dsolve(eqn)
S = dsolve(eqn,cond)
[y1,...,yN] = dsolve(___)

句法解释：

S＝dsolve（eqn）求解微分方程eqn，其中eqn是符号方程。使用diff和==表示微分方程。例如，diff（y，x）==y表示等式dy/dx=y。通过将方程指定为微分方程的向量来求解微分方程组。
例子：
解方程：
d y d t = a y \frac{\mathrm{d}y}{\mathrm{d}t}=ay dtdy​=ay

syms a y(t)
eqn = diff(y,t) == a*y;
dsolve(eqn)

ans =
C1*exp(a*t)

解高阶方程：
d 2 y d t 2 = a y \frac{\mathrm{d^{2}}y}{\mathrm{d}t^{2}}=ay dt2d2y​=ay

syms y(t) a
eqn = diff(y,t,2) == a*y;
ySol(t) = dsolve(eqn)

ySol(t) =
C2*exp(-a^(1/2)*t) + C3*exp(a^(1/2)*t)

S＝dsolve（eqn，cond）用初始或边界条件cond求解方程。
例子：
解如下方程：
d y d t = a y \frac{\mathrm{d}y}{\mathrm{d}t}=ay dtdy​=ay
且已知条件：
y （ 0 ） = 5 y（0）=5 y（0）=5

syms y(t) a
eqn = diff(y,t) == a*y;
cond = y(0) == 5;
ySol(t) = dsolve(eqn,cond)

ySol(t) =
5*exp(a*t)

解高阶方程：
d 2 y d t 2 = a 2 y \frac{\mathrm{d^{2}}y}{\mathrm{d}t^{2}}=a^{2}y dt2d2y​=a2y
且条件：
y ( 0 ) = b , y ′ ( 0 ) = 1 y(0)=b,y'(0)=1 y(0)=b,y′(0)=1

syms y(t) a b
eqn = diff(y,t,2) == a^2*y;
Dy = diff(y,t);
cond = [y(0)==b, Dy(0)==1];
ySol(t) = dsolve(eqn,cond)

ySol(t) =
(exp(a*t)*(a*b + 1))/(2*a) + (exp(-a*t)*(a*b - 1))/(2*a)

[y1，…，yN]=dsolve（__）将解分配给变量y1，…，yN。

例子：
解方程组：
{ d y d t = z d z d t = − y \begin{cases} \begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}=z\\ \frac{\mathrm{d}z}{\mathrm{d}t}=-y \end{aligned} \end{cases} ⎩ ⎨ ⎧​dtdy​=zdtdz​=−y​​

syms y(t) z(t)
eqns = [diff(y,t)==z, diff(z,t)==-y];
[ySol(t) zSol(t)] = dsolve(eqns)

ySol(t) =
C2*cos(t) + C1*sin(t)
zSol(t) =
C1*cos(t) - C2*sin(t)

fourier：傅里叶变换——将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。
F=fourier（f）是符号表达式的傅立叶变换或具有默认自变量x的函数f。默认情况下，结果F是w的函数。如果f=f（w），则F作为变量v的函数返回F＝F（v）。
F=fourier（f，v）返回F作为变量v的函数而不是默认变量w。
F=fourier（f，u，v）将F视为变量u的函数而不是默认变量x。

syms t v w x f(x)
     fourier(1/t)   returns   -pi*sign(w)*1i
     fourier(exp(-x^2),x,t)   returns   pi^(1/2)*exp(-t^2/4)
     fourier(exp(-t)*heaviside(t),v)   returns   1/(1+v*1i)
     fourier(diff(f(x)),x,w)   returns   w*fourier(f(x),x,w)*1i

ifourier：傅里叶逆变换
f＝ifourier（F）是符号的傅立叶逆变换。带有默认自变量w的表达式或函数F。结果f默认是x的函数。如果F＝F（x），则f作为变量t的函数返回，f＝f（t）。
f=ifourier（F，u）返回f作为变量u的函数,而不是默认变量x。
f=ifourier（F，v，u）将F视为变量v的函数而不是默认变量w。
例如：

syms t u v w f(x)
     ifourier(w*exp(-3*w)*heaviside(w))  returns  1/(2*pi*(-3+x*1i)^2)
     ifourier(1/(1 + w^2),u)   returns   exp(-abs(u))/2
     ifourier(v/(1 + w^2),v,u)   returns   -(dirac(1,u)*1i)/(w^2+1)
     ifourier(fourier(f(x),x,w),w,x)   returns   f(x)

laplace：以实现信号f(t)的拉普拉斯变换
L=laplace (f) 是符号函数f的拉普拉斯变换，默认返回函数L是关于s的函数。
L=laplace (f,t) 是符号函数f的拉普拉斯变换，返回函数L是关于t的函数。
L=laplace (f,w,z) 是关于w的函数f的拉普拉斯变换，返回函数L是关于z的函数。
函数调用实例

syms a s t w x
       laplace(t^5)                 returns   120/s^6
       laplace(exp(a*s))             returns   1/(t-a)
       laplace(sin(w*x),t)            returns   w/(t^2+w^2)
       laplace(cos(x*w),w,t)          returns   t/(t^2+x^2)
       laplace(x^sym(3/2),t)          returns   3/4*pi^(1/2)/t^(5/2)
       laplace(diff(sym('F(t)')))        returns   laplace(F(t),t,s)*s-F(0)

ilaplace：可以实现信号F(s)的拉普拉斯逆变换
F = ilaplace(L) 是函数L(s)的拉普拉斯逆变换，默认返回函数F是关于t的函数。
F = ilaplace(L,y) 是函数L(s)的拉普拉斯逆变换，返回函数F是关于y的函数。
F = ilaplace(L,y,x) 返回函数F是关于x的函数。
函数调用实例

 syms s t w x y
       ilaplace(1/(s-1))                  returns   exp(t)
       ilaplace(1/(t^2+1))                returns   sin(x)
       ilaplace(t^(-sym(5/2)),x)            returns   4/3/pi^(1/2)*x^(3/2)
       ilaplace(y/(y^2 + w^2),y,x)          returns   cos(w*x)
       ilaplace(sym('laplace(F(x),x,s)'),s,x)   returns   F(x)

ztrans:实现信号f(k)的z变换
F = ztrans (f) 是函数f(n)的z变换，默认返回函数F是关于z的函数。
F = ztrans (f,w) 是函数f(n)的z变换，返回函数F是关于w的函数。
F = ztrans (f,k,w) 是函数f(k)的z变换，返回函数F是关于w的函数。
函数调用范例

syms k n w z
ztrans(2^n)                returns  z/(z-2)
ztrans(sin(k*n),w)          returns  sin(k)*w/(1-2*w*cos(k)+w^2)
ztrans(cos(n*k),k,z)         returns  z*(-cos(n)+z)/(-2*z*cos(n)+z^2+1)
ztrans(cos(n*k),n,w)         returns  w*(-cos(k)+w)/(-2*w*cos(k)+w^2+1)
ztrans(sym('f(n+1)'))         returns  z*ztrans(f(n),n,z)-f(0)*z

iztrans:实现信号F(z)的逆z变换
f = iztrans (F) 是函数F(z)的逆z变换，默认返回函数f是关于n的函数。
f = iztrans (F,k) 是函数F(z)的逆z变换，返回函数f是关于k的函数。
f = iztrans (F,w,k) 是函数F(w)的逆z变换，返回函数f是关于k的函数。
函数调用范例：

syms z x k f(n)
iztrans(z/(z-2))        returns   2^n
iztrans(sin(1/n))  returns  -(1i^(k-1)*((-1)^k-1))/(2*factorial(k))
iztrans(exp(x/z),z,k)    returns   x^k/k
iztrans(ztrans(f(n),n,z),z,k)  returns  f(k)

（3）
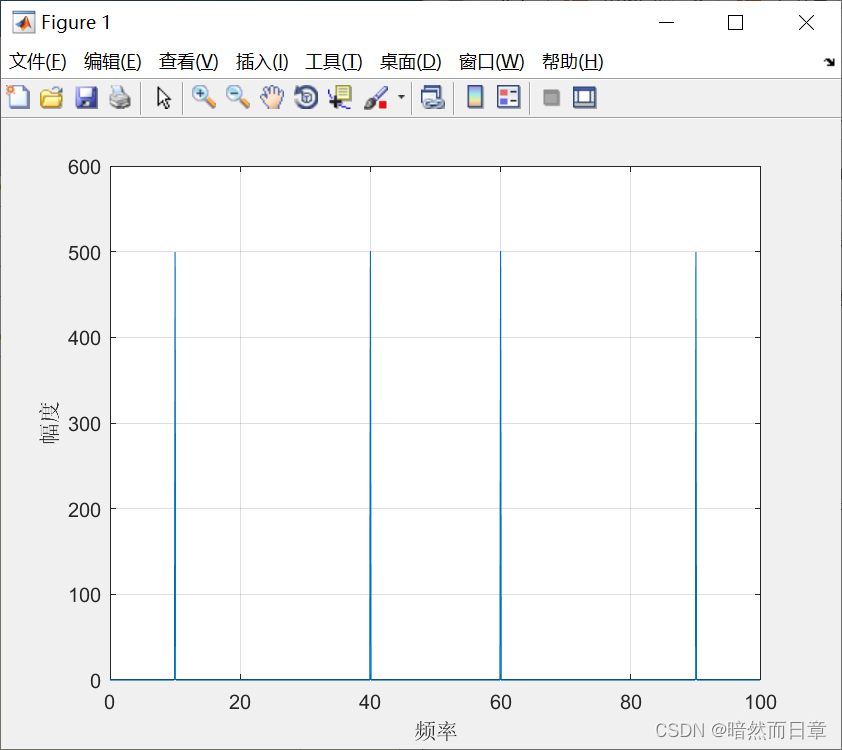
对函数x=sin(20πt)+sin(80πt)做傅里叶变换

t=0:1/100:10-1/100;
x=sin(2*pi*10*t)+sin(2*pi*40*t);
y=fft(x);
m=abs(y);
f=(0:numel(y)-1)'*100/numel(y);
plot(f,m);
grid on;
ylabel('幅度');
xlabel('频率');

在这里插入图片描述

3、运算结果的可视化函数调用范例

要求：

将运算结果表达成更为直观的图形化形式，是MATLAB的一个重要功能，便于直观地理解一些比较抽象的概念和理论分析结果。一般来说，图形化表示应基于数值运算的结果，但对于符号运算结果，MATLAB也定义了一些直接基于解析表达式来绘图的函数。
运算结果图形化表示时需要特别注意的一个问题，是绘图坐标轴范围的合理选取问题：图形化表示的坐标范围总是有限的，应该在有限的绘图区间内，充分展现所关注的运算结果的特征。绘图坐标范围太小或者区间选择不合理，不能完整展现运算结果的特征；坐标范围太大，则无关图形太多，特征图形太小，其特性展现不突出。
（1）基于数值运算结果的常用可视化函数。了解plot（二维曲线）、plot3（三维曲线）、surf（三维阴影曲面）、mesh（三维网格曲面）、stem（二维离散序列）、stem3（三维离散序列）等常用图形化函数的功能和用法，并举例展示。
（2）基于符号运算结果的常用可视化函数。了解ezplot（二维曲线）、ezplot3（三维曲线）、ezsurf（三维阴影曲面）、ezmesh（三维网格曲面）等基于解析表达式的图形化函数的功能和用法，并利用这些函数分别绘制dsolve（求解微分方程）、fourier（傅里叶变换）、laplace（拉普拉斯变换）等符号函数运算结果的图形，注意根据需要选择适当的函数、维数和绘图坐标轴范围。
（3）给定一个函数（自定），分别用符号运算和数字运算的方式求其傅里叶变换，然后分别基于数值运算和符号运算结果绘图，注意选择适当的数值计算范围和绘图坐标轴范围。

解答：

（1）
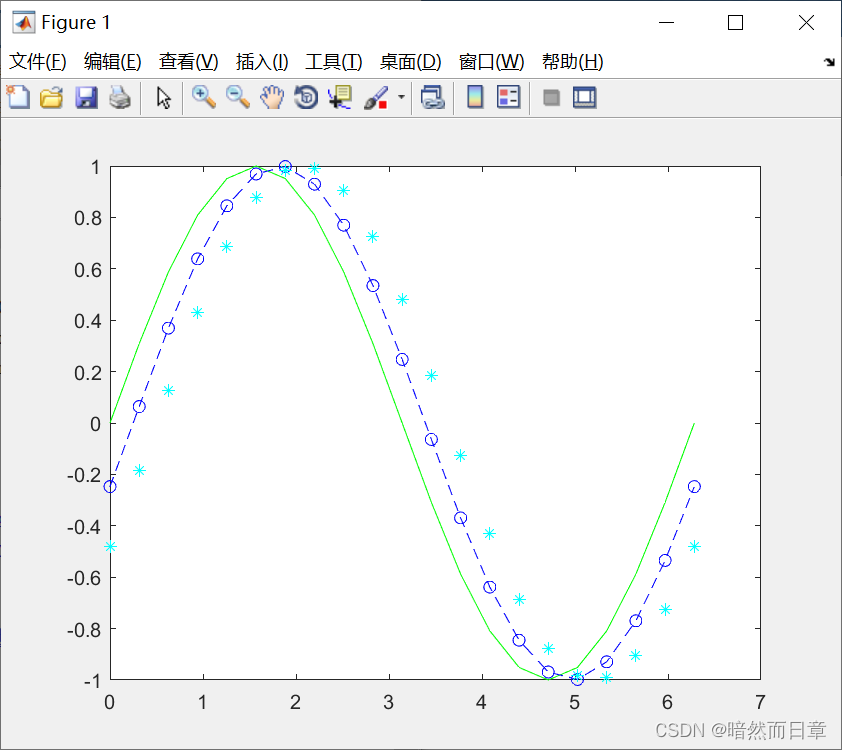
plot

x = 0:pi/10:2*pi;
y1 = sin(x);
y2 = sin(x-0.25);
y3 = sin(x-0.5);

figure
plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')

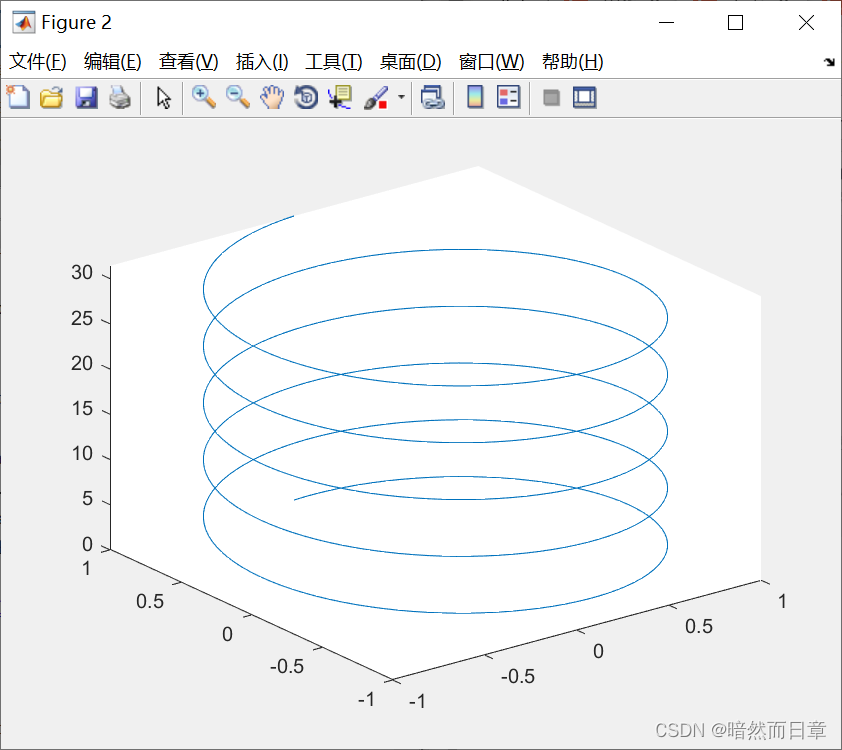
在这里插入图片描述
plot3

t = 0:pi/50:10*pi;
st = sin(t);
ct = cos(t);

figure
plot3(st,ct,t)

在这里插入图片描述
surf

[X,Y] = meshgrid(1:0.5:10,1:20);
Z = sin(X) + cos(Y);
surf(X,Y,Z)

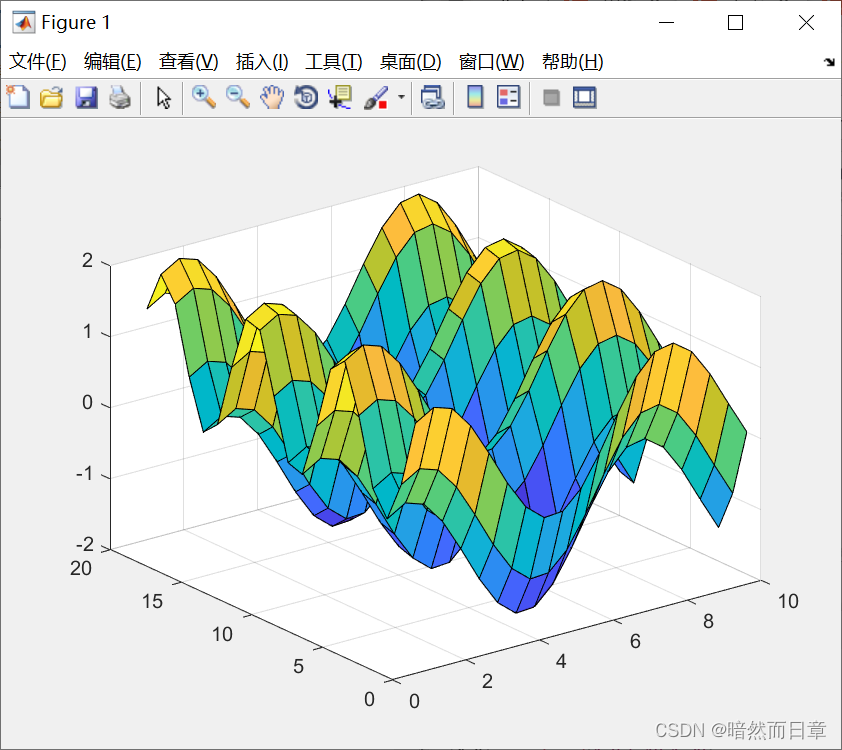
在这里插入图片描述
mesh

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R)./R;
C = gradient(Z);

figure
mesh(X,Y,Z,C)

在这里插入图片描述
stem

figure
X = linspace(0,2*pi,25)';
Y = (cos(2*X));
stem(X,Y,'LineStyle','-.',...
     'MarkerFaceColor','red',...
     'MarkerEdgeColor','green')

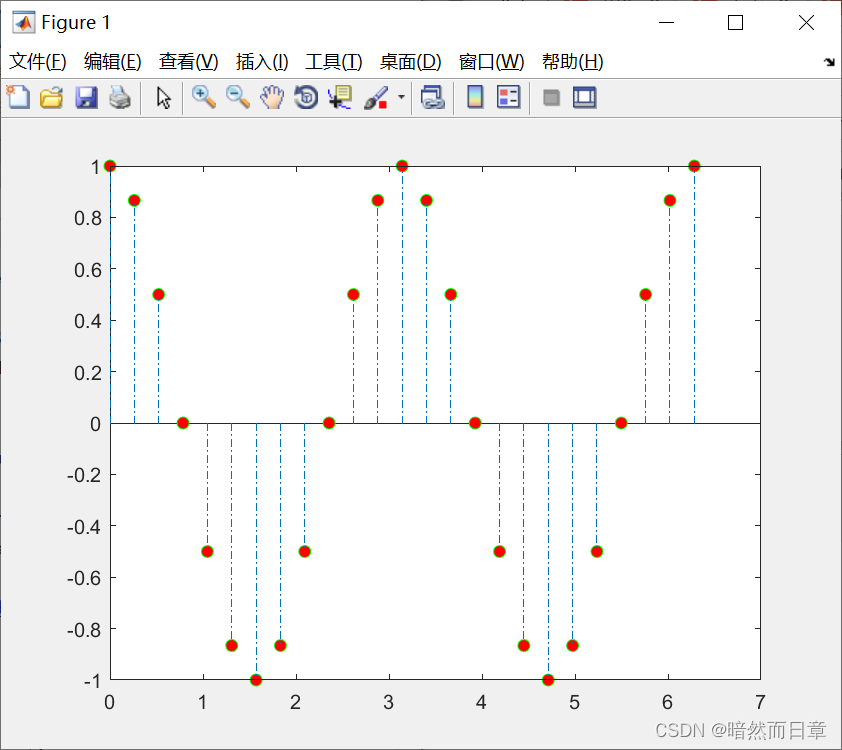
在这里插入图片描述
stem3

figure
theta = linspace(0,2*pi);
X = cos(theta);
Y = sin(theta);
Z = theta;
stem3(X,Y,Z,':*m')

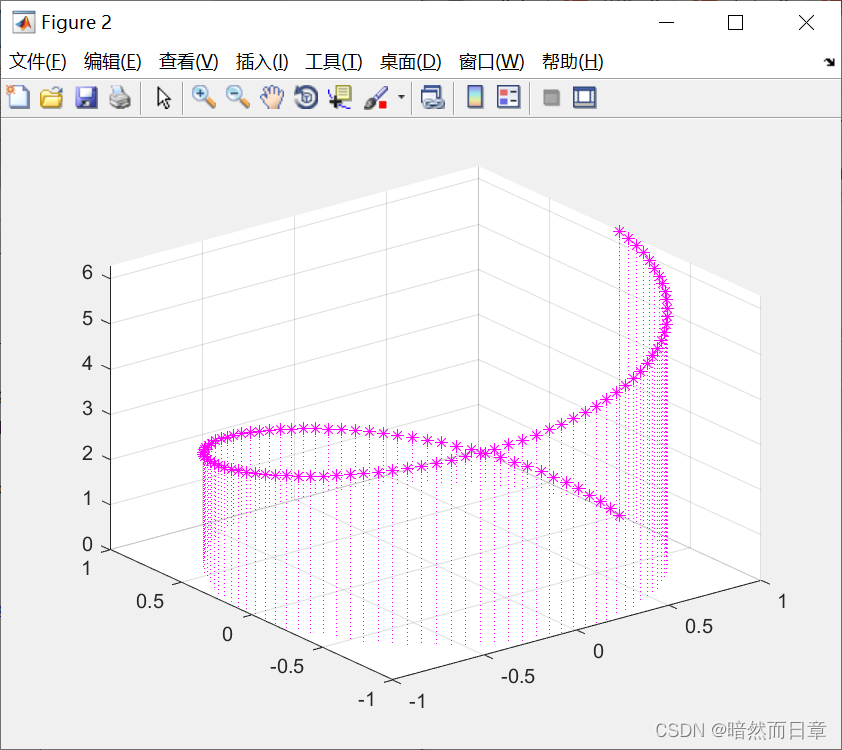
在这里插入图片描述

（2）
ezplot

ezplot('x^2-y^4')

在这里插入图片描述
ezplot3

ezplot3('sin(t)','cos(t)','t',[0,6*pi])

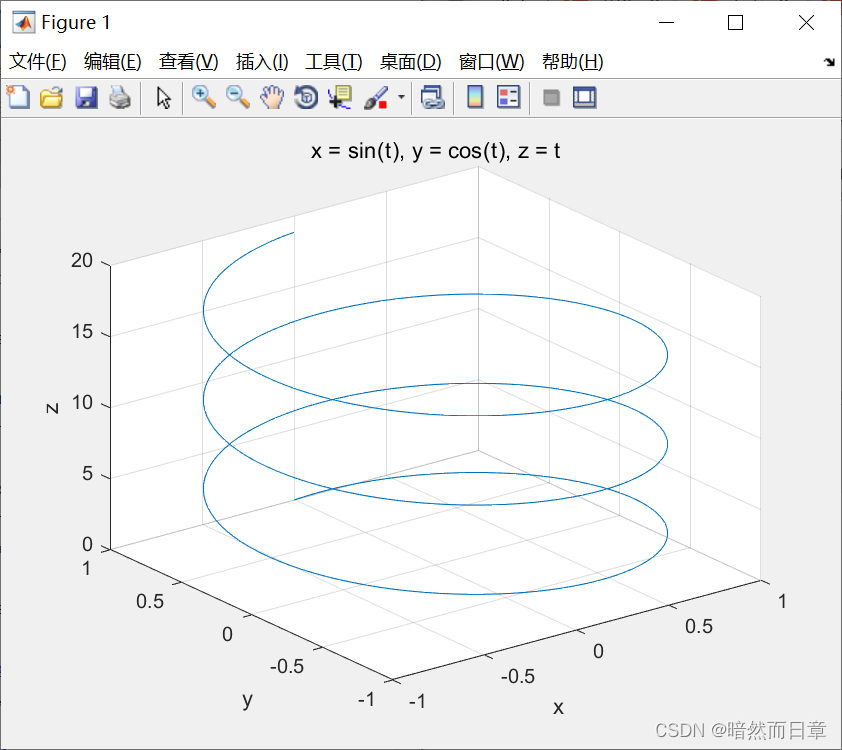
在这里插入图片描述

ezsurf

ezsurf('sqrt(1-x^2-y^2)')

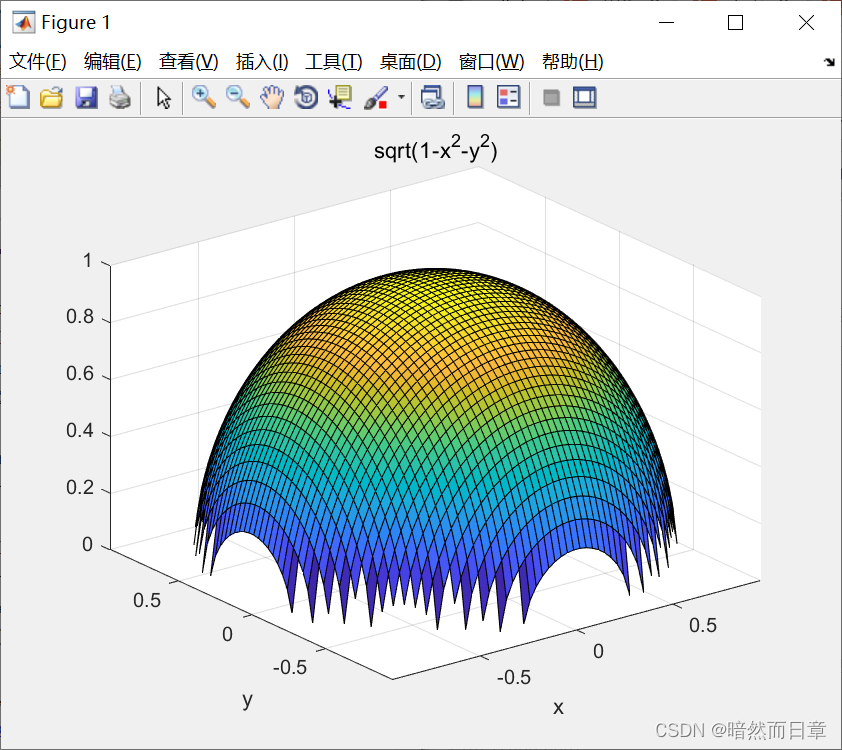
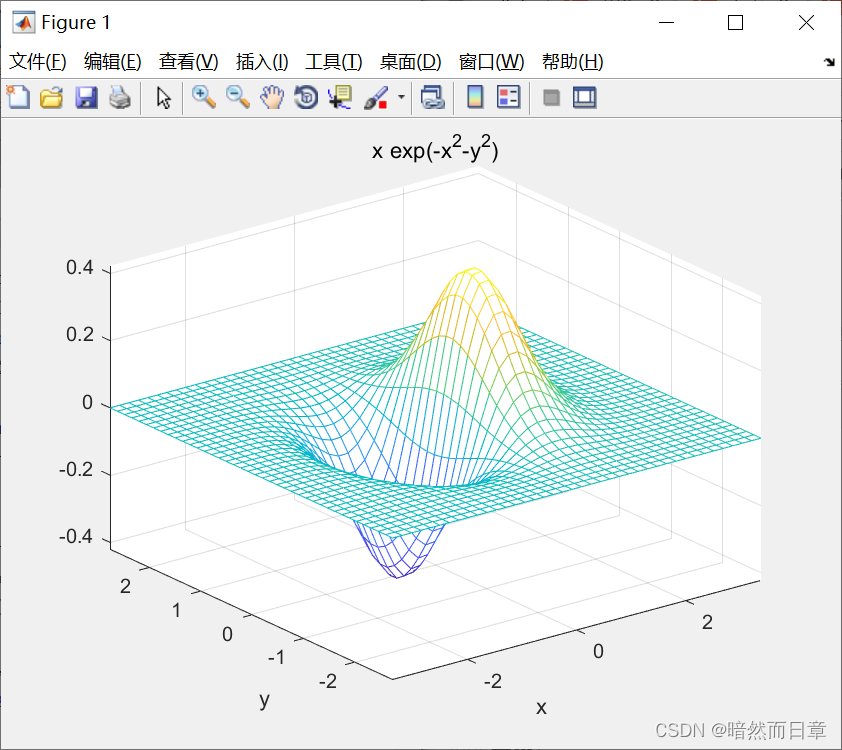
在这里插入图片描述
ezmesh

fh = @(x,y) x.*exp(-x.^2-y.^2);
ezmesh(fh,40)

在这里插入图片描述

（3）

暂无，欢迎贡献分享

4、音频信号采集和保存、回放

要求：

MATLAB可以调用电脑的声卡进行音频信号的采集和回放。自行查阅相关资料，了解基于audiorecorder对象的音频采集、保存（含保存为音频文件）、音频文件读取、回放等功能的程序实现方法，并举例说明。

解答：

music=audiorecorder(8000,16,2);
%创建一个保存音频信息的对象，它包含采样率，时间和录制的音频信息等等。
%44100表示采样为44100Hz（可改为8000, 11025, 22050等，
%此数值越大，录入的声音质量越好，相应需要的存储空间越大）
%16为用16bits存储，2为两通道即立体声（也可以改为1即单声道）。

recordblocking(music,5);
%开始录制，此时对着麦克风说话即可,录制时间为5秒。
play(music);

MyRecording=getaudiodata(music);
%得到以n*2列数字矩阵存储的刚录制的音频信号。
plot(MyRecording);

filename='myspeech.wav';
audiowrite(filename,MyRecording,8000);
%MyRecording表示要存入的波形矩阵，
%8000表采样率，'myspeech'为存储的文件名
[y, fs]=audioread('myspeech.wav');

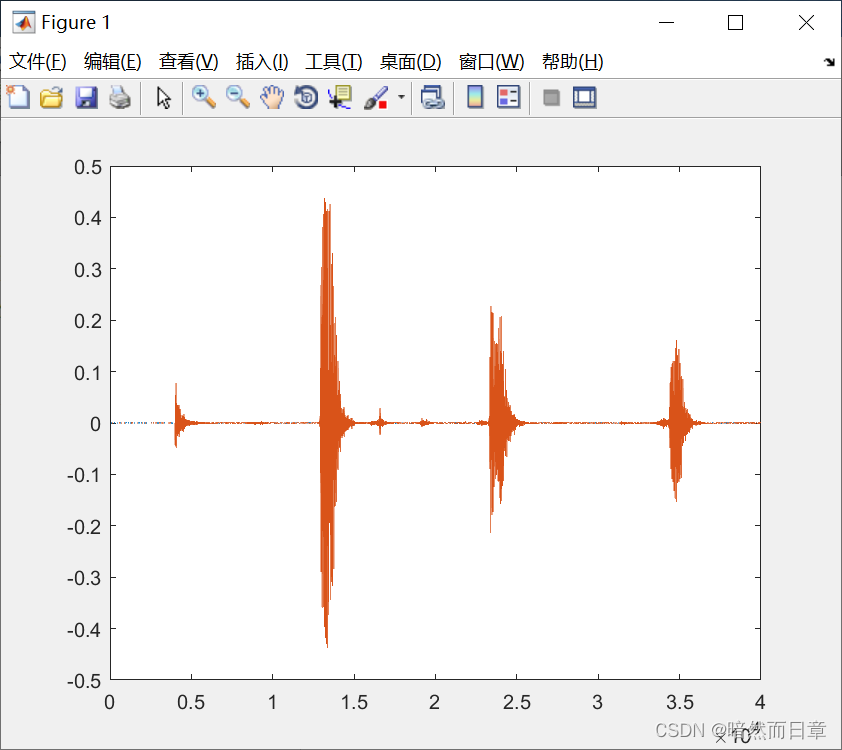
在这里插入图片描述

5、帮助和错误提示

要求：

（1）MATLAB内部定义了大量的功能函数供用户使用，当用户不清楚函数的功能和用法时，可以在命令行窗口用“help 函数名”查看该函数的帮助信息，并通过其中的链接了解该函数的更多细节（英文）。请举例说明help命令的使用。
（2）当执行的MATLAB命令（直接在命令行运行）或者脚本存在错误时，MATLAB会给出相应的错误提示，以便用户排除错误。请查阅网络资料，了解MATLAB中常见的错误提示及其产生的原因，并通过例子说明其中的一些错误。

解答：

（1）
在这里插入图片描述
（2）
在这里插入图片描述

三、反思总结

3（3）暂无

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1318074.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MYSQL练题笔记-高级字符串函数 / 正则表达式 / 子句-简单3题

MYSQL练题笔记-高级字符串函数 / 正则表达式 / 子句-简单3题

这个系列先写了三题，比较简单写在一起。 1.修复表中的名字相关的表和题目如下 看题目就知道是有关字符串函数的，于是在书里查询相关的函数，如下图，但是没有完全对口的函数，所以我还是去百度了。 然后发现结合上面的4个…
阅读更多...
C#教程（三）：字符串的各种用法

C#教程（三）：字符串的各种用法

在C#中，字符串（string 类型）是一种常用的数据类型，用于存储和操作文本数据。以下是一些C#中字符串的常见用法 1、输出任意的字符串长度 代码 #region 输出任意的字符串长度 Console.WriteLine("请输入你心中想到的名字&…
阅读更多...
html+css+javascript实现渐隐轮播

html+css+javascript实现渐隐轮播

实现效果： 图片自动轮播，点击左右按钮会操作图片向前或向后，图片与小圆点相互呼应，具有交互效果。 编写思想： 实现交互时使用了排他思想，同选项卡的功能； 自动轮播采用了setInterval()&#…
阅读更多...
Python 全栈体系【四阶】（六）

Python 全栈体系【四阶】（六）

第四章 机器学习 五、线性模型 1. 概述 线性模型是自然界最简单的模型之一，它描述了一个（或多个）自变量对另一个因变量的影响是呈简单的比例、线性关系。例如： 住房每平米单价为 1 万元，100 平米住房价格为 100 万…
阅读更多...
发现隐藏的 Web 应用程序漏洞

发现隐藏的 Web 应用程序漏洞

随着 Web 2.0 的扩展，近年来社交媒体平台、电子商务网站和电子邮件客户端充斥着互联网空间，Web 应用程序已变得无处不在。 国际知名网络安全专家、东方联盟创始人郭盛华透露：‘应用程序消耗和存储更加敏感和全面的数据，它们成为对…
阅读更多...
MIT6.S081-实验准备

MIT6.S081-实验准备

实验全程在Vmware虚拟机 (镜像：Ubuntu-20.04-beta-desktop-amd64) 中进行 一、版本控制 1.1 将mit的实验代码克隆到本地 git clone git://g.csail.mit.edu/xv6-labs-2020 1.2 修改本地git配置文件 创建github仓库，记录仓库地址 我的仓库地址就是htt…
阅读更多...
国内最好的开源MES/免费MES/低代码MES

国内最好的开源MES/免费MES/低代码MES

一、系统概述： 万界星空科技免费MES、开源MES、商业开源MES、市面上最好的开源MES、MES源代码、适合二开的开源MES、功能最全的开源MES、好看的数字大屏、开源自动排班系统、开源质检系统。 1.万界星空开源MES制造执行系统的Java开源版本。 开源mes系统包括系统管…
阅读更多...
Java与前端：风云变幻的技术之路

Java与前端：风云变幻的技术之路

前言 近日，有关“Java已死、前端已凉”的言论在IT圈内流传甚广，引起了广泛关注和讨论。这究竟是真相还是一场对技术人员的焦虑贩卖呢？让我们一同探讨这场技术风暴带来的变化与机遇，并分享一些实用的建议。 一、技术变革的常态 …
阅读更多...
0x31 质数

0x31 质数

0x31 质数 定义： 若一个正整数无法被除了1和它自身之外的任何自然数整除，则称该数为质数（或素数），否则则称该正整数为合数。 在整个自然数集合中，质数的数量不多，分布比较稀疏，对…
阅读更多...
Support Vector Machine(SVM)——支持向量机

Support Vector Machine(SVM)——支持向量机

1.从逻辑回归到SVM 回顾一下逻辑回归的模型 然后经过sigmoid函数得到预测y1的概率，sigmoid函数如下图 对于单个样本来说损失函数如下 当一个输入的真实标签为1时，损失函数就只剩，如左图所示,我们想要让，来使损失函数尽可能的小 对…
阅读更多...
实验报告九、使用枚举法验证6174猜想

实验报告九、使用枚举法验证6174猜想

一、实验目的： 1、了解6174猜想的内容。 2、熟练使用选择结构和循环结构。 3、了解标准库itertools中combinations()函数的用法。 4、熟练使用字符串的join（方法。 5、熟练使用内置函数int()、str()、 sorted()。 二、实验内容： 1955…
阅读更多...
机器学习的数据管理

机器学习的数据管理

.机器学习的数据管理注意事项 机器学习的生命周期包括如下部分 (1).业务的理解，机器学习问题框架 (2).数据理解和收集 (3).模型的训练和评估 (4)模型部署 (5).模型监控 (6).业务衡量 数据管理和机器学习的生命周期的2，3，4个阶段有关。…
阅读更多...
Pikachu漏洞练习平台之暴力破解（基于burpsuite）

Pikachu漏洞练习平台之暴力破解（基于burpsuite）

从来没有哪个时代的黑客像今天一样热衷于猜解密码 ---奥斯特洛夫斯基 Burte Force（暴力破解）概述 “暴力破解”是一攻击具手段，在web攻击中，一般会使用这种手段对应用系统的认证信息进行获取。 其过程就是使用大量的认证信息在认…
阅读更多...
【STM32】STM32学习笔记-EXTI外部中断(11)

【STM32】STM32学习笔记-EXTI外部中断(11)

00. 目录 文章目录 00. 目录01. 中断系统02. 中断执行流程03. STM32中断04. NVIC基本结构05. NVIC优先级分组06. EXTI简介07. EXTI基本结构08. AFIO复用IO口09. EXTI框图10. 计数器模块11. 旋转编码器简介12. 附录 01. 中断系统 中断：在主程序运行过程中&#xff0…
阅读更多...
使用PyQt5连接mysql数据库实现用户管理（增，删，改，查,附代码和完整界面）

使用PyQt5连接mysql数据库实现用户管理（增，删，改，查,附代码和完整界面）

一：环境搭建 首先本地需要安装python,PyQt5环境，我是用pip安装的 python -m pip install PyQt5 或者 pip install PyQt5 python -m pip install PyQt5-tools 或者 pip install PyQt5-tools 如果网络不好，还可以使用其他源 pip install PyQt…
阅读更多...
C++中的继承(一)

C++中的继承(一)

文章目录 前言概念访问限定符基类和派生类的赋值转换继承中的作用域派生类的默认成员函数构造函数 拷贝构造析构函数 继承的其他一些细节 前言 我们之前说过，继承是面向对象的三大特性。 面向对象的三大特性： 封装、继承、多态。 封装在类和对象体现出…
阅读更多...
大一python题库刷题训练,大一python填空题题库

大一python题库刷题训练,大一python填空题题库

大家好，给大家分享一下大一python题库及答案和分析，很多人还不知道这一点。下面详细解释一下。现在让我们来看看！ 这篇文章主要介绍了大一python上机题库及答案，具有一定借鉴价值，需要的朋友可以参考下。希望大家阅读完…
阅读更多...
【线性代数】期末速通！

【线性代数】期末速通！

1. 行列式的性质 1.1 求一个行列式的值 特殊地，对角线左下全为0，结果为对角线乘积。行 r 列 c 1.2 性质 某行（列）加上或减去另一行（列）的几倍，行列式不变某行（列）乘 …
阅读更多...
智能优化算法应用：基于海洋捕食者算法3D无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用：基于海洋捕食者算法3D无线传感器网络(WSN)覆盖优化 - 附代码

智能优化算法应用：基于海洋捕食者算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用：基于海洋捕食者算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.海洋捕食者算法4.实验参数设定5.算法…
阅读更多...
git-lfs基本知识讲解

git-lfs基本知识讲解

目录 1. 基本知识2. 安装 1. 基本知识 git-lfs 是 Git Large File Storage 的缩写，是 Git 的一个扩展，用于处理大文件的版本控制。 它允许你有效地管理和存储大型二进制文件，而不会使 Git 仓库变得过大和不稳定。以下是一些与 git-lfs 相关…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023