【算法】bfs与dfs算法解决FloodFill（洪流）问题（C++）

文章目录

1. 什么是FloodFill问题
2. 用什么方法解决FloodFill问题
3. 具体例题
- 773.图像渲染
- 200.岛屿数量
- 695.岛屿的最大面积
- 130.被围绕的区域

1. 什么是FloodFill问题

一般floodfill问题可以描述为：给定一个二维矩阵，其中每个元素代表一个像素点，并给定一个起始点、目标颜色和填充颜色。问题要求将以起始点为中心，与其相邻且具有相同颜色的所有区域都填充为目标颜色。

在这里插入图片描述

2. 用什么方法解决FloodFill问题

我们通常使用下面两种方法解决FloodFill算法问题：

DFS（深搜）算法通常使用递归实现，在处理当前像素点的相邻像素点时，递归调用 DFS 函数，不断深入直到无法找到相邻像素为止。

BFS （宽搜）算法通常使用队列实现，将起始像素点加入队列中，并不断扩展队列中的像素点，直到队列为空为止。

下面直接结合例题来理解两种解题方法。

3. 具体例题

第一道题 “图像渲染” 是下面例题中作为基座的一道题，讲解会尽量详细，后面的题

773.图像渲染

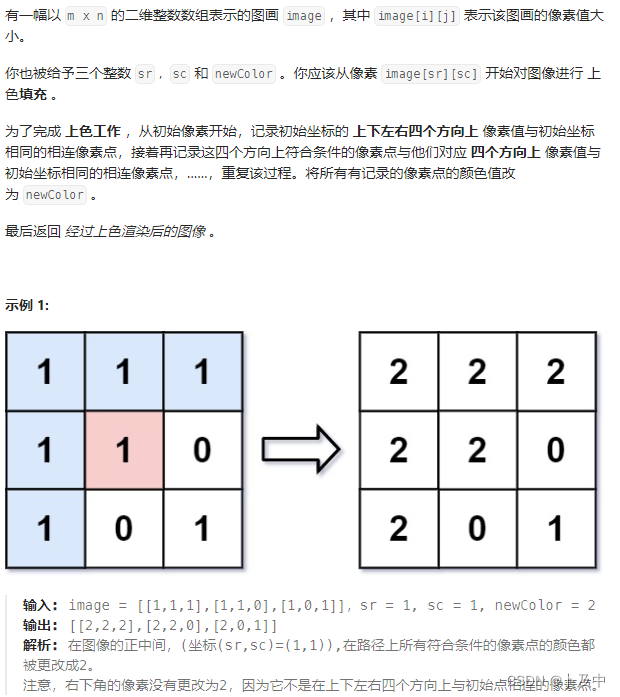
题意分析

即对于一个矩阵，我们随机选取一个元素，将该元素与对于其有相同值的上下左右 的元素（对上下左右的元素继续找上下左右）均上色为color。本质上就是找区域内的相邻元素。

解法

DFS（深度优先搜索）

“搜索一个位置的上下左右坐标，并对其上下左右坐标继续搜索上下左右坐标” 的过程可以理解为将一个主问题分解为多个子问题的过程，适用递归解决。

我们知道：深度优先搜索即一条路走到死，而该递归过程也是深搜的思想。

思路

先记录题目给我们的当前位置的颜色prevColor，如果当前位置=color，则直接返回
以当前位置开始，直接进行递归操作
- 对于递归函数：先将当前位置上色，随后遍历上下左右四个方向的元素，每遍历到一个元素
- 对该元素进行进行dfs操作，即可完成对 相连像素点的上色

代码

class Solution {
private:
    int dx[4] = {0, 0, -1, 1}; // 用于计算上下左右位置的下标
    int dy[4] = {-1, 1, 0, 0};
    int m, n, _color, prevColor; // 定义成全局变量方便调用（也可以传参）

    // dfs: 查看 坐标(x, y) 上下左右四个元素，并更改颜色
    void dfs(vector<vector<int>>& image, int x, int y) {
        image[x][y] = _color; // 当前位置上色
        for(int k = 0; k < 4; ++k) {
            int nx = x + dx[k]; // 计算一个方向的坐标
            int ny = y + dy[k];
            // 确保不越界 以及 值相同
            if(nx >= 0 && nx < m && ny >= 0 && ny < n && image[nx][ny] == prevColor)
                dfs(image, nx, ny); // 递归找连结的需要上色的像素
        }
    }

public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        prevColor = image[sr][sc]; // 记录最开始 / 当前元素颜色
        if(prevColor == color) return image; // 如果当前像素已经是所需颜色，则直接返回矩阵

        m = image.size(), n = image[0].size();
        _color = color;

        dfs(image, sr, sc);

        return image;
    }
};

BFS（宽度优先搜索）

宽度优先搜索利用队列和循环，每次将坐标入队，随后将其上下左右四个坐标入队，通过每次取队列元素，持续该过程，直到队列为空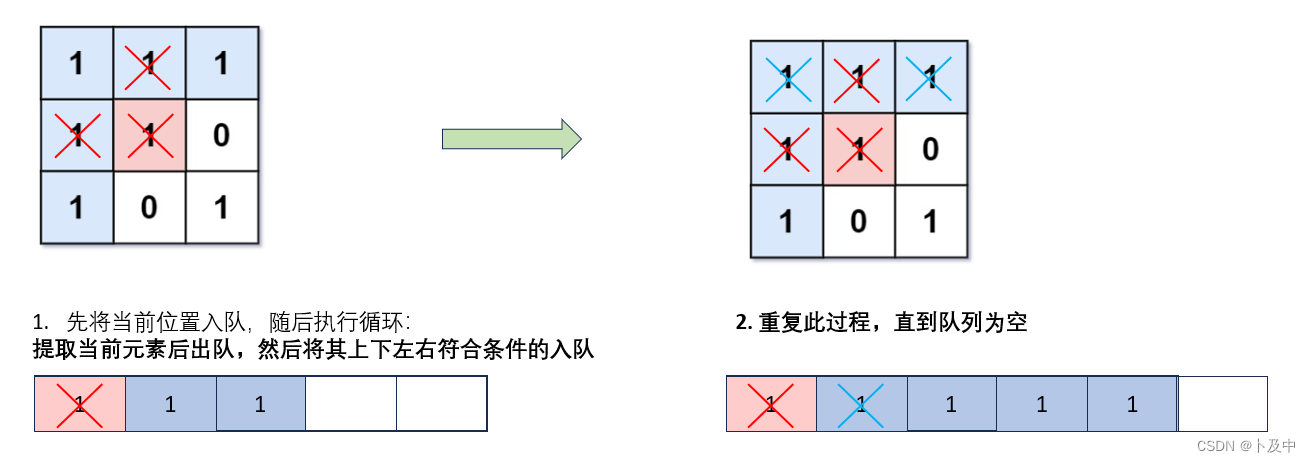

思路

先记录当前位置的颜色prevColor，如果当前位置=color，则直接返回
将当前位置坐标入队，每次提取当前元素的坐标，并将其上色
将上下左右四个方向的元素（符合条件的）入队，重复此过程

代码

class Solution {
public:
    typedef pair<int, int> pii;
    int dx[4] = {0, 0, -1, 1}; // 查询当前像素的上下左右时，xy坐标的更改
    int dy[4] = {-1, 1, 0, 0};

    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        // 边界情况
        int tmp = image[sr][sc]; // 记录要更改的像素值
        if(tmp == color) return image;
        
        queue<pii> q; // 存储像素坐标
        q.push({sr, sc});
        while(!q.empty())
        {
            auto [a, b] = q.front(); // 提取当前像素坐标
            q.pop();
            image[a][b] = color; // 上色（更改像素值）
            for(int i = 0; i < 4; ++i)
            {
                int x = a + dx[i];
                int y = b + dy[i];
                // 如果未越界则入队
                if(x >= 0 && x < image.size() && y >= 0 && y < image[0].size() && image[x][y] == tmp)
                    q.push({x, y});
            }
        }

        return image;
    }
};

200.岛屿数量

题意分析

矩阵由’1’, ‘0’ 两个元素组成，每一块相连的1（横着竖着相连）组成的区域为一个岛屿，我们需要找到矩阵中岛屿的数量。

解法

DFS（深度优先搜索）

思路

首先我们定义visit数组，用于记录矩阵中每一位元素是否已经被遍历过，如果为true，则不去执行该位的操作。
遍历整个矩阵，对于矩阵的每个（符合要求的）元素都执行dfs算法
每次循环中dfs彻底结束，则统计出了一片岛屿，++ret（最终结果）
关于此题的dfs：
- 用于将矩阵中坐标为（x, y）的元素及其上下左右的元素标记

代码

class Solution {
private:
    int ret = 0; // 定义为全局变量，方便dfs改动和调用
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {-1, 1, 0, 0};
    int m, n;
    vector<vector<bool>> visit; // 存储网格是否被检索过的信息

private:
    // 通过递归，将当前位置的岛屿统计出来
    // dfs： 将grid[x][y] 位置所在的岛屿统计出来
    void dfs(vector<vector<char>>& grid, int x, int y) {
        // 将当前位置检索设置为true
        visit[x][y] = true;
        for(int i = 0; i < 4; ++i)
        {
            int nx = x + dx[i];
            int ny = y + dy[i];
            if((nx >= 0 && nx < m) && (ny >= 0 && ny < n) && !visit[nx][ny] && grid[nx][ny] == '1')
            {
                dfs(grid, nx, ny);
            }
        }
    }

public:
    int numIslands(vector<vector<char>>& grid) {
        m = grid.size(), n = grid[0].size();
        visit.resize(m, vector<bool>(n, false)); // 初始化visit数组
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(!visit[i][j] && grid[i][j] == '1') // 该位置并未检索过且值为1
                {
                    ++ret;
                    dfs(grid, i, j);
                }
            }
        }
        return ret;
    }
};

BFS（宽度优先搜索）

思路

这里宽搜和深搜的代码非常相似，只需要将bfs代码内部将递归改为使用队列即可，具体代码中注解，不再多余解释

代码

class Solution {
public:
    int ret = 0;
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {-1, 1, 0, 0};
    int m, n;
    vector<vector<bool>> visit; // 存储网格是否被检索过的信息

    void bfs(vector<vector<char>>& grid, int x, int y) {
        queue<pair<int, int>> q; // 存储位置坐标
        
        q.push({x, y});
        while(!q.empty())
        {
            auto [a, b] = q.front(); // 取出队头元素
            q.pop();
            for(int k = 0; k < 4; ++k) // 遍历该位置的上下左右四个位置
            {
                int nx = a + dx[k];
                int ny = b + dy[k];
                if((nx >= 0 && nx < m) && (ny >= 0 && ny < n) && !visit[nx][ny] && grid[nx][ny] == '1')
                {
                    q.push({nx, ny});
                    visit[nx][ny] = true;
                }
            }
        }
    }

    int numIslands(vector<vector<char>>& grid) {
        m = grid.size(), n = grid[0].size();
        visit.resize(m, vector<bool>(n, false));

        // 遍历矩阵
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(!visit[i][j] && grid[i][j] == '1')
                {
                    ++ret;
                    bfs(grid, i, j);
                }
            }
        }

        return ret;
    }
};

695.岛屿的最大面积

题意分析

该题和上一题（岛屿数量）在解法和思路上可以说非常相似，只是前者要求岛屿数量，而后者要求岛屿最大面积，我们只需定义一个变量，每次统计一个岛屿后比较并更新该变量即可。

解法

DFS（深度优先搜索）

思路

重复：该题和上一题（岛屿数量）在解法和思路上可以说非常相似，只是前者要求岛屿数量，而后者要求岛屿最大面积，我们只需定义一个变量，每次统计一个岛屿后比较并更新该变量即可。

所以重点在于ret何时统计：

对于深搜，我们每次执行当前递归函数彻底结束后，执行ret = max(count, ret);即更新最大面积。
因为递归函数结束后，此时count记录的就是新岛屿的面积，则在dfs后更新最大面积。

代码

class Solution {
private:
    vector<vector<bool>> visit;
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {-1, 1, 0, 0};
    int ret = 0, count = 0; // 统计岛屿面积
    int m, n;

public:
    void dfs(vector<vector<int>>& grid, int x, int y) {
        visit[x][y] = true; // 将当前位置检索设置为true
        for(int k = 0; k < 4; ++k)
        {
            int nx = x + dx[k];
            int ny = y + dy[k];
            if((nx >= 0 && nx < m) && (ny >= 0 && ny < n) && !visit[nx][ny] && grid[nx][ny] == 1) // 判断是否合法
            {
                ++count;
                dfs(grid, nx, ny);
            }
        }   
    }

    int maxAreaOfIsland(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        visit.resize(m, vector<bool>(n, false));

        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                count = 1; // 当前位置开始（从1开始）
                if(!visit[i][j] && grid[i][j] == 1)
                {
                    dfs(grid, i, j);
                    ret = max(count, ret); // 找到最大面积
                }
            }
        }

        return ret;
    }
};

BFS（宽度优先搜索）

思路

ret何时统计：

对于宽搜，我们每次执行一次bfs函数后，进行ret = max(ret, count),
因为执行dfs后，count的值就是新岛屿的面积，所以我们在其后判断更新最大面积。

代码

class Solution {
private:
    typedef pair<int, int> pii;
    vector<vector<bool>> visit;
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {-1, 1, 0, 0};
    int ret = 0, count = 0; // 统计岛屿面积
    int m, n;

public:
    void bfs(vector<vector<int>>& grid, int x, int y) {
        visit[x][y] = true; // 将当前位置检索设置为true
        queue<pii> q; // 队列存储坐标
        q.push({x, y}); // 将起始坐标添加到队列中
        while(!q.empty()) // 广度优先搜索
        {
            auto [x, y] = q.front();
            q.pop();
            for(int k = 0; k < 4; ++k)
            {
                int nx = x + dx[k];
                int ny = y + dy[k];
                if((nx >= 0 && nx < m) && (ny >= 0 && ny < n) && !visit[nx][ny] && grid[nx][ny] == 1) // 判断是否合法
                {
                    ++count;
                    visit[nx][ny] = true;
                    q.push({nx, ny}); // 将新的岛屿坐标添加到队列中
                }
            }
        }   
    }

    int maxAreaOfIsland(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        visit.resize(m, vector<bool>(n, false));

        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                count = 1; // 当前位置开始（从1开始）
                if(!visit[i][j] && grid[i][j] == 1)
                {
                    bfs(grid, i, j);
                    ret = max(ret, count);
                }
            }   
        }

        return ret;
    }
};

130.被围绕的区域

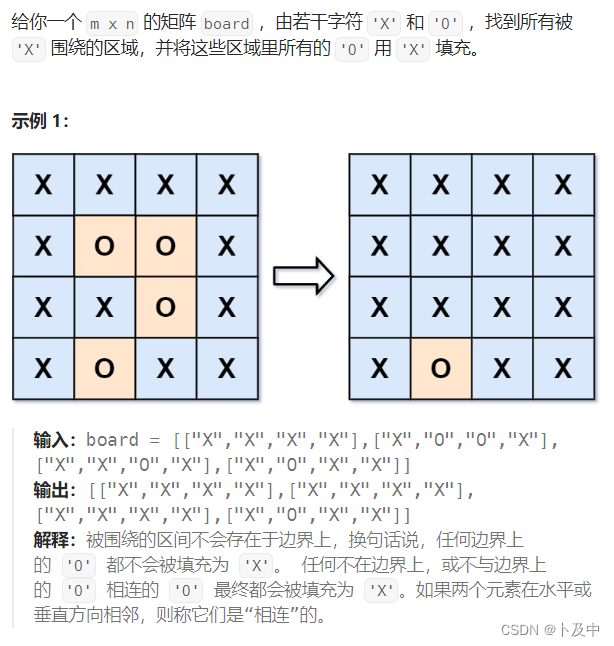
题意分析

题目要求我们找到所有被’X’围绕的’O’，并将其改为’X’
- 被’X’围绕的’O’：
正难则反：我们直接找到被’X’围绕的’O’是有难度的，则可以逆转思维：
- 找到所有不被’X’包围的’O’，将这些’O’改为’T’（改成任意字符）
- 随后遍历矩阵，将所有’O’改为’X’，此时即完成了题目要求
- 最后将’T’再改回X即可

解法

DFS（深度优先搜索）

思路

根据题意分析的思路讲解，首先遍历矩阵四边，对边缘元素执行dfs函数
- dfs: 用于将当前位置联结的’O’改为’T’
当循环+dfs 全部执行完毕，此时四边相连的’O’已经被改为’T’
遍历矩阵，将剩余的’O’改为’X’，将’T’改为’O’。

代码

class Solution {
public:
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {-1, 1, 0, 0};
    int m, n;

    // dfs将当前位置周围的'O'改为'T'
    void dfs(vector<vector<char>>& board, int x, int y) {
        board[x][y] = 'T';
        for(int k = 0; k < 4; ++k)
        {
            int a = x + dx[k];
            int b = y + dy[k];
            if((a >= 0 && a < m) && (b >= 0 && b < n) && board[a][b] == 'O') // 保证合法性
            {
                dfs(board, a, b);
            }
        }
    }

    void solve(vector<vector<char>>& board) {
        m = board.size(), n = board[0].size();

        // 正难则反（将未被'X'围绕的'O'更改，然后遍历矩阵找'O'）
        // 1. 矩阵四边周围的'O' 改为 'T'
        for(int i = 0; i < m; ++i) // 上下边
        {
            if(board[i][0] == 'O') dfs(board, i, 0);
            if(board[i][n - 1] == 'O') dfs(board, i, n - 1);
        }
        for(int j = 0; j < n; ++j) // 左右边
        {
            if(board[0][j] == 'O') dfs(board, 0, j);
            if(board[m - 1][j] == 'O') dfs(board, m - 1, j);
        }

        // 2. 还原：将'O'改为'X' / 将'T'改为'O'
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(board[i][j] == 'O') board[i][j] = 'X';
                if(board[i][j] == 'T') board[i][j] = 'O';
            }
        }
    }
};

BFS（宽度优先搜索）

思路

和前面的题一致，我们用队列进行宽搜的实现：

首先创建visit数组，用于记录矩阵中的每位是否被遍历过
除了bfs函数思路不同，其余与dfs完全一致，这里主要在于bfs的写法：
- 先将当前位置入队，并在visit中改为true
- 只要队列不为空，持续获取上下左右方向的元素，符合要求的入队更改为true，持续此过程。

代码

class Solution {
public:
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {-1, 1, 0, 0};
    vector<vector<bool>> visit;
    int m, n;

    // bfs将当前位置周围的'O'改为'T'
    void bfs(vector<vector<char>>& board, int x, int y) {
        queue<pair<int, int>> q;
        visit[x][y] = true;
        board[x][y] = 'T';
        q.push({x, y}); // 将起始位置入队
        while(!q.empty())
        {
            auto [x, y] = q.front();
            q.pop();
            for(int k = 0; k < 4; ++k)
            {
                int nx = x + dx[k];
                int ny = y + dy[k];
            if((nx >= 0 && nx < m) && (ny >= 0 && ny < n) && !visit[nx][ny] && board[nx][ny] == 'O')
                {
                    board[nx][ny] = 'T'; // 将'O'改为'T'
                    visit[nx][ny] = true; // 修改为单等号
                    q.push({nx, ny});
                }
            }
        }
    }

    void solve(vector<vector<char>>& board) {
        m = board.size(), n = board[0].size();
        visit.resize(m, vector<bool>(n, false)); // bfs算法中记录该位置是否被检查过

        // 正难则反（将未被'X'围绕的'O'更改，然后遍历矩阵找'O'）
        // 1. 矩阵四边周围的'O' 改为 'T'
        for(int i = 0; i < m; ++i) // 上下边
        {
            if(board[i][0] == 'O') bfs(board, i, 0);
            if(board[i][n - 1] == 'O') bfs(board, i, n - 1);
        }
        for(int j = 0; j < n; ++j) // 左右边
        {
            if(board[0][j] == 'O') bfs(board, 0, j);
            if(board[m - 1][j] == 'O') bfs(board, m - 1, j);
        }

        // 2. 还原：将'O'改为'X' / 将'T'改为'O'
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(board[i][j] == 'O') board[i][j] = 'X';
                if(board[i][j] == 'T') board[i][j] = 'O';
            }
        }
    }
};