需求分析

假设有n个村庄，有些村庄之间有连接的路，有些村庄之间并没有连接的路

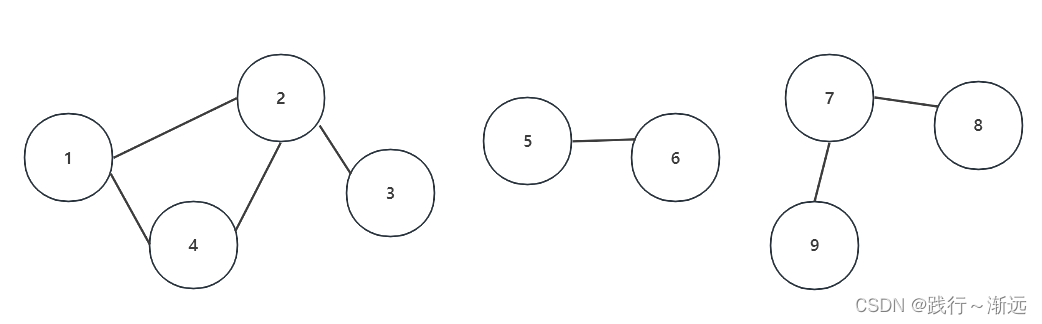
请你设计一个数据结构，能够快速执行2个操作

1. ◼ 查询2个村庄之间是否有连接的路
2. ◼ 连接2个村庄

首先思考在现有的数据结构能否实现上面的功能，数组、链表、平衡二叉树、集合（Set）？貌似可以，但是查询、连接的时间复杂度都是：O(n)，杀鸡用牛刀的感觉！

引出我们今天提出的数据结构并查集，并查集能够办到查询、连接的均摊时间复杂度都是 O（ α n） ，α n < 5，可以认为是常数级别。并查集非常适合解决这类“连接”相关的问题。

并查集（Union Find）

详细介绍：https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Time_complexity
并查集也叫作不相交集合（Disjoint Set）
并查集有2个核心操作

1. ◼ 查找（Find）：查找元素所在的集合（这里的集合并不是特指Set这种数据结构，是指广义的数据集合）
2. ◼ 合并（Union）：将两个元素所在的集合合并为一个集合

◼ 并查集核心接口定义如下：

public interface Union<V>{
	void find(V v1);   //查找
	void union(V v1,V v2);    //合并
}

实现思路

1. ◼ Quick Find 查找时间复杂度为O（1），合并时间复杂度O（n）
2. ◼ Quick Union 查找（Find）的时间复杂度：O(logn)，可以优化至 O（a(n)）,a(n)<5;合并（Union）的时间复杂度：O(logn),可以优化至 O（a(n)）,a(n)<5;

所以我们一般采用第二种Quick Union的思路。

如何存储数据？

假设并查集处理的数据都是整型，那么可以用整型数组来存储数据，一开始，默认一个村庄单独作为一个集合（自己指向自己），之后再通过union 的形式连接 【初始化时，每个元素各自属于一个单元素集合】

连接之后

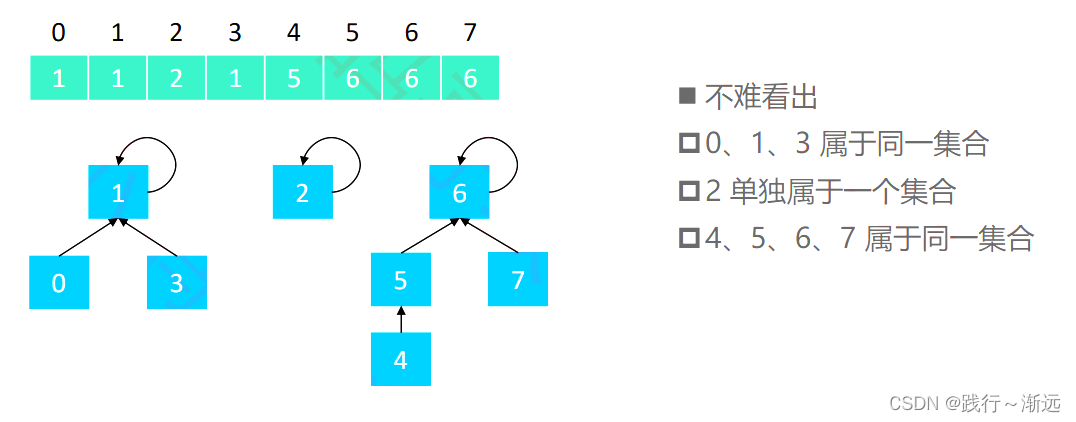
因此，并查集是可以用数组实现的树形结构（二叉堆、优先级队列也是可以用数组实现的树形结构）

---

代码实现（quick union为例，基于ranks的优化【union】，基于路径分裂的优化【find】）

初始化
初始化时，每个元素各自属于一个单元素集合（自己指向自己）


Quick Union 的 union(v1, v2)：让 v1 的根节点指向 v2 的根节点或者v2的根节点指向v1的根节点，这里就有优化的空间了，到底是谁嫁接到谁身上呢？我们的想法是树低的嫁接到树高的节点，这样不会让树的高度变高，搜索的效率可以提高。因此我们还需要维护一个树的高度的数组ranks。初始值高度均为1
因此上面的初始化代码改造为：

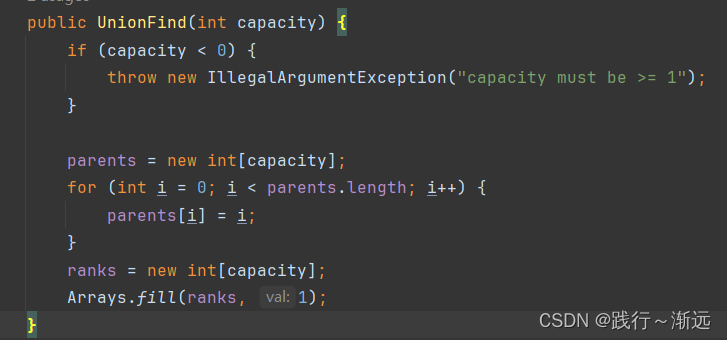
◼ union函数的实现

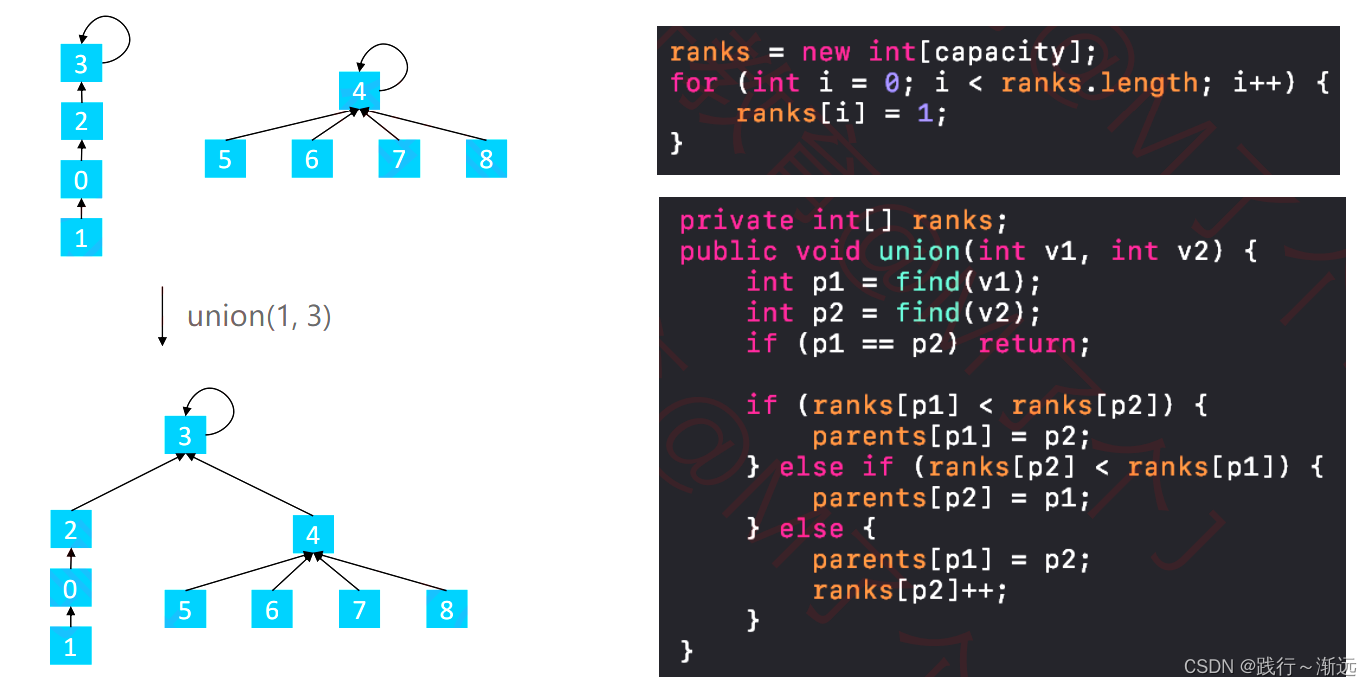
Quick Union 的 find(v1)：找到 v1 的根节点，这里就有优化的空间了，在往上找的过程中，可以降低树的高度，采用路径分裂的思路，将路径上的每一个节点都指向其祖父节点，从而降低树的高度。当然有一种路径压缩的方案，就是将所有节点均指向根节点，这个成本有点高，我们折中考虑采用路径分裂。

◼ find函数的实现

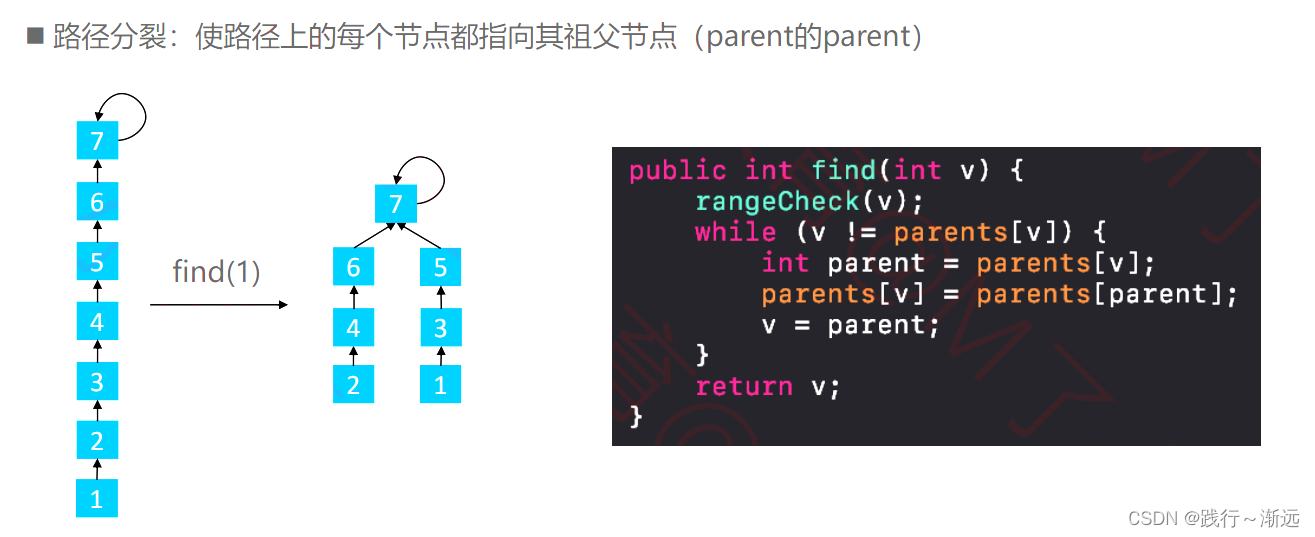
完整代码如下

class Union{
    int[] parenrs;
    int[] ranks;

    public Union(int cap){
        parenrs = new int[cap];
        ranks = new int[cap];
 		for (int i = 0; i < parents.length; i++) {
			parents[i] = i;
		}
		Arrays.fill(ranks,1);
    }
    public int find(int v){
        while(v!=parenrs[v]){
            int p = parenrs[v];
            parenrs[v] = parenrs[p];
            v = p;
        }
        return v;
    }
    public void union(int a,int b){
        int ap = find(a);
        int bp = find(b);
        if(ap==bp){
            return;
        }
        if(ranks[ap]>ranks[bp]){
            parenrs[bp] = ap;
        }else if(ranks[ap]<ranks[bp]){
            parenrs[ap] = bp;
        }else{  
            parenrs[ap] = bp;
            ranks[bp]+=1;
        }

    }
    public boolean isSame(int a,int b){
        return find(a) == find(b);
    }
}

测试代码

	@Test
    public void testTime() {
		Unionu = new Union(100000);
		uf.union(0, 1);
		uf.union(0, 3);
		uf.union(0, 4);
		uf.union(2, 3);
		uf.union(2, 5);
		
		uf.union(6, 7);

		uf.union(8, 10);
		uf.union(9, 10);
		uf.union(9, 11);
		
		Asserts.test(!uf.isSame(2, 7));

		uf.union(4, 6);
		
		Asserts.test(uf.isSame(2, 7));
		
		Times.test(uf.getClass().getSimpleName(), () -> {
			for (int i = 0; i < count; i++) {
				uf.union((int)(Math.random() * count), 
						(int)(Math.random() * count));
			}
			
			for (int i = 0; i < count; i++) {
				uf.isSame((int)(Math.random() * count), 
						(int)(Math.random() * count));
			}
		});
	}

class Asserts {
	public static void test(boolean value) {
		try {
			if (!value) throw new Exception("测试未通过");
		} catch (Exception e) {
			e.printStackTrace();
		}
	}
}
class Times {
	private static final SimpleDateFormat fmt = new SimpleDateFormat("HH:mm:ss.SSS");
	
	public interface Task {
		void execute();
	}
	
	public static void test(String title, Task task) {
		if (task == null) return;
		title = (title == null) ? "" : ("【" + title + "】");
		System.out.println(title);
		System.out.println("开始：" + fmt.format(new Date()));
		long begin = System.currentTimeMillis();
		task.execute();
		long end = System.currentTimeMillis();
		System.out.println("结束：" + fmt.format(new Date()));
		double delta = (end - begin) / 1000.0;
		System.out.println("耗时：" + delta + "秒");
		System.out.println("-------------------------------------");
	}
}