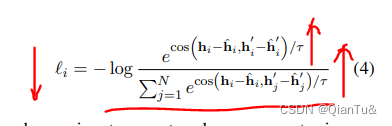简介

CFD的核心问题是求解双曲偏微分方程
$\frac{\partial}{\partial t} u(x, t)+\frac{\partial}{\partial x} f(u(x, t))=0$ 在CFD中，双曲偏微分方程一般使用Godunov型迎风格式求解。但是这种迎风格式往往实施起来比较复杂（需要特征分解），如果能使用中心格式实现离散，则可以简化编程、提高计算效率。

Kurganov-Tadmor格式¹（简称KT）可以实现二阶精度，是一种中心离散格式。根据此格式openFoam开发了rhoCentralFoam求解器，以求解可压缩流。本文仅介绍格式的推导思路，具体在openFoam中的实现方法将由后续文章给出。

KT格式有两种形式，它们的推导方式如下：
（1）全离散形式由分片线性解积分所得。
（2）半离散形式由Rusanov离散格式演化而来。

全离散格式

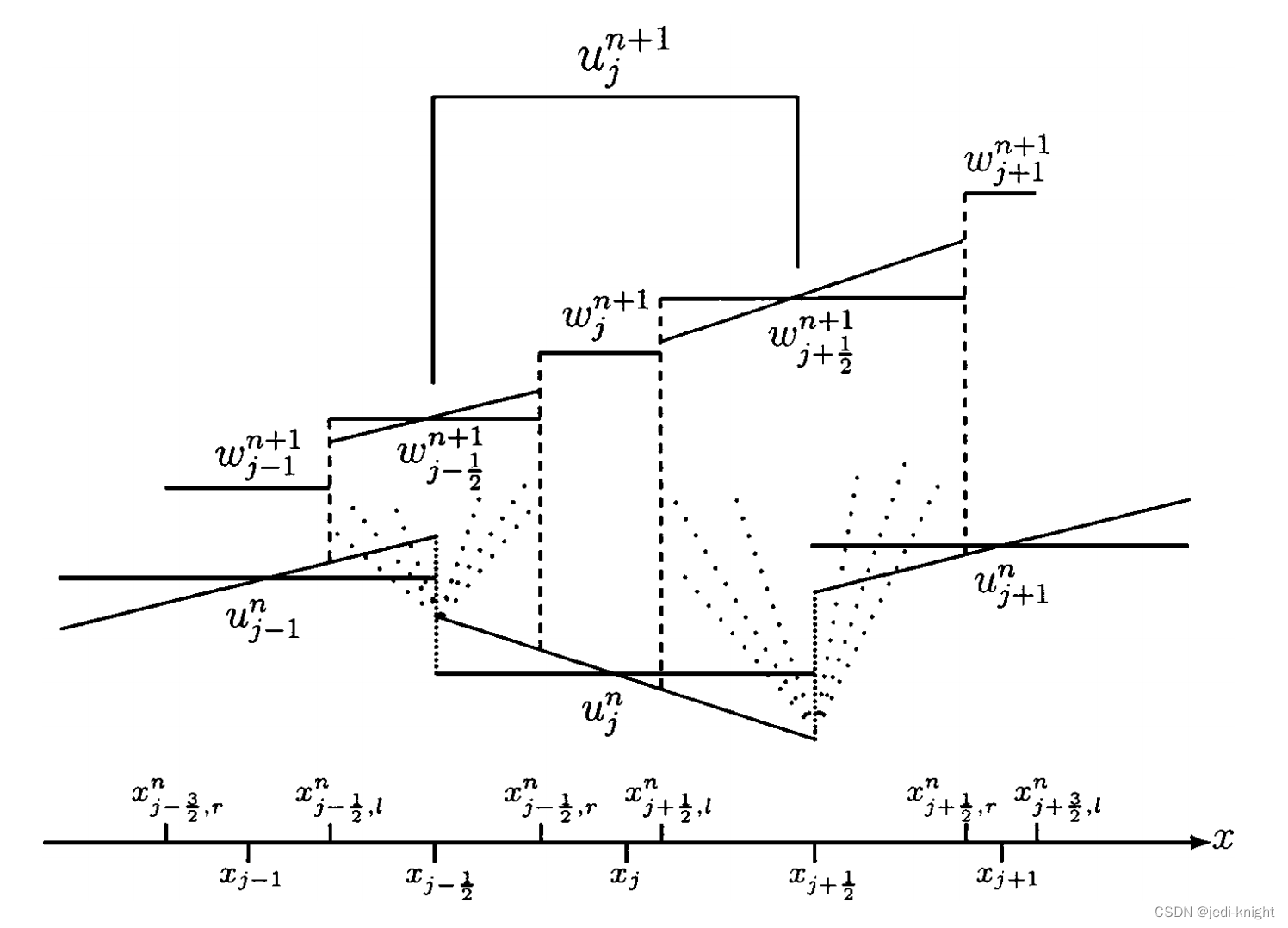在这里插入图片描述使用分片线性函数完成解的重构，重构后的解为
$\tilde{u}\left(x, t^{n}\right):=\sum_{j}\left[\bar{u}_{j}^{n}+\left(u_{x}\right)_{j}^{n}\left(x-x_{j}\right)\right] \mathbf{1}_{\left[x_{j-1 / 2}, x_{j+1 / 2}\right]}, \quad x_{j \pm 1 / 2}:=x_{j} \pm \frac{\Delta x}{2}$
图中 $x_{j + {1 \over 2},l}^n$ 表示在一个时间步后，扰动由 ${x_{j + {1 \over 2}}}$ 向左传播到的位置。所以有
${x_{j + {1 \over 2}}} - x_{j + {1 \over 2},l}^n = a_{j + {1 \over 2}}^n\Delta t$ 同理有
$x_{j + {1 \over 2},r}^n - {x_{j + {1 \over 2}}} = a_{j + {1 \over 2}}^n\Delta t$ 式中 $a_{j + {1 \over 2}}^n$ 是界面处扰动的传播速度。可使用朗金-雨果纽关系式确定。

(1) 在 $\left[ {x_{j + {1 \over 2},l}^n,x_{j + {1 \over 2},r}^n} \right] \times \left[ {{t^n},{t^{n + 1}}} \right]$ 范围内，对双曲守恒方程积分可得

$\begin{aligned} w_{j+1 / 2}^{n+1}= & \frac{u_{j}^{n}+u_{j+1}^{n}}{2}+\frac{\Delta x-a_{j+1 / 2}^{n} \Delta t}{4}\left(\left(u_{x}\right)_{j}^{n}-\left(u_{x}\right)_{j+1}^{n}\right) \\ & -\frac{1}{2 a_{j+1 / 2}^{n}}\left[f\left(u_{j+1 / 2, r}^{n+1 / 2}\right)-f\left(u_{j+1 / 2, l}^{n+1 / 2}\right)\right], \end{aligned}$
式中， $w_{j+1 / 2}^{n+1}$ 表示 $\left[ {x_{j + {1 \over 2},l}^n,x_{j + {1 \over 2},r}^n} \right]$ 范围内的平均积分结果，上角标 $n + 1/2$ 表示半时间步，可用泰勒展开近似
$u_{j+1 / 2, l}^{n+1 / 2}:=u_{j+1 / 2, l}^{n}-\frac{\Delta t}{2} f\left(u_{j+1 / 2, l}^{n}\right)_{x}, \quad u_{j+1 / 2, l}^{n}:=u_{j}^{n}+\Delta x\left(u_{x}\right)_{j}^{n}\left(\frac{1}{2}-\lambda a_{j+1 / 2}^{n}\right)$ 同理有
$u_{j+1 / 2, r}^{n+1 / 2}:=u_{j+1 / 2, r}^{n}-\frac{\Delta t}{2} f\left(u_{j+1 / 2, r}^{n}\right)_{x}, \quad u_{j+1 / 2, r}^{n}:=u_{j+1}^{n}-\Delta x\left(u_{x}\right)_{j+1}^{n}\left(\frac{1}{2}-\lambda a_{j+1 / 2}^{n}\right)$

(2) 在 $\left[ {x_{j - {1 \over 2},r}^n,x_{j + {1 \over 2},l}^n} \right] \times \left[ {{t^n},{t^{n + 1}}} \right]$ 范围内，对双曲守恒方程积分可得
$\begin{aligned} w_{j}^{n+1}= & u_{j}^{n}+\frac{\Delta t}{2}\left(a_{j-1 / 2}^{n}-a_{j+1 / 2}^{n}\right)\left(u_{x}\right)_{j}^{n} \\ & -\frac{\lambda}{1-\lambda\left(a_{j-1 / 2}^{n}+a_{j+1 / 2}^{n}\right)}\left[f\left(u_{j+1 / 2, l}^{n+1 / 2}\right)-f\left(u_{j-1 / 2, r}^{n+1 / 2}\right)\right] \end{aligned}$

综上得到了区间 $\left[ {x_{j + {1 \over 2},l}^n,x_{j + {1 \over 2},r}^n} \right]$ 与区间 $\left[ {x_{j - {1 \over 2},r}^n,x_{j + {1 \over 2},l}^n} \right]$ 上解的均值。

为了得到最终的 $u_j^{n + 1}$ ,需要将区间 $\left[ {x_{j - {1 \over 2}}^n,x_{j - {1 \over 2},r}^n} \right]$ 、区间 $\left[ {x_{j - {1 \over 2},r}^n,x_{j + {1 \over 2},l}^n} \right]$ 和 $\left[ {x_{j + {1 \over 2},l}^n,x_{j + {1 \over 2}}^n} \right]$ 的解积分平均，最终得到
$\begin{aligned} u_{j}^{n+1}= & \frac{1}{\Delta x} \int_{x_{j-1 / 2}}^{x_{j+1 / 2}} \tilde{w}\left(\xi, t^{n+1}\right) d \xi=\lambda a_{j-1 / 2}^{n} w_{j-1 / 2}^{n+1}+\left[1-\lambda\left(a_{j-1 / 2}^{n}+a_{j+1 / 2}^{n}\right)\right] w_{j}^{n+1} \\ & +\lambda a_{j+1 / 2}^{n} w_{j+1 / 2}^{n+1}+\frac{\Delta x}{2}\left[\left(\lambda a_{j-1 / 2}^{n}\right)^{2}\left(u_{x}\right)_{j-1 / 2}^{n+1}-\left(\lambda a_{j+1 / 2}^{n}\right)^{2}\left(u_{x}\right)_{j+1 / 2}^{n+1}\right] \end{aligned}$
这就是全离散K-T格式，具体的minmod斜率限制器可参见论文原文。斜率限制器的目的是使得此二阶格式TVD，在间断解处退回一阶格式。

半离散格式

半离散格式的推导相对简单，首先考虑一阶Rusanov格式
$u_{j}^{n+1}=u_{j}^{n}-\frac{\lambda}{2}\left[f\left(u_{j+1}^{n}\right)-f\left(u_{j-1}^{n}\right)\right]+\frac{1}{2}\left[\lambda a_{j+1 / 2}^{n}\left(u_{j+1}^{n}-u_{j}^{n}\right)-\lambda a_{j-1 / 2}^{n}\left(u_{j}^{n}-u_{j-1}^{n}\right)\right]$
将其写为半离散格式（左端项是时间导数）
${{\partial u} \over {\partial t}} = - {1 \over {\Delta x}}\left( {{{f\left( {u_{j + 1}^n} \right) - f\left( {u_{j - 1}^n} \right)} \over 2} - {{a_{j + 1/2}^n\left( {u_{j + 1}^n - u_j^n} \right) - a_{j - 1/2}^n\left( {u_j^n - u_{j - 1}^n} \right)} \over 2}} \right)$
进一步写为守恒形式
${{\partial u} \over {\partial t}} = - {1 \over {\Delta x}}\left( {{H_{j + {1 \over 2}}} - {H_{j - {1 \over 2}}}} \right)$ 其中
${H_{j + {1 \over 2}}} = {{f\left( {u_{j + 1}^n} \right) + f\left( {u_j^n} \right)} \over 2} - {{a_{j + 1/2}^n} \over 2}\left( {u_{j + 1}^n - u_j^n} \right)$ ${H_{j - {1 \over 2}}} = {{f\left( {u_j^n} \right) + f\left( {u_{j - 1}^n} \right)} \over 2} - {{a_{j - 1/2}^n} \over 2}\left( {u_j^n - u_{j - 1}^n} \right)$
为了将格式提升为二阶，则使用分段线性将解重构，有
$H_{j+1 / 2}(t):=\frac{f\left(u_{j+1 / 2}^{+}(t)\right)+f\left(u_{j+1 / 2}^{-}(t)\right)}{2}-\frac{a_{j+1 / 2}(t)}{2}\left[u_{j+1 / 2}^{+}(t)-u_{j+1 / 2}^{-}(t)\right]$
式中
$u_{j+1 / 2}^{+}:=u_{j+1}(t)-\frac{\Delta x}{2}\left(u_{x}\right)_{j+1}(t), \quad u_{j+1 / 2}^{-}:=u_{j}(t)+\frac{\Delta x}{2}\left(u_{x}\right)_{j}(t)$
$H_{j-1 / 2}$ 的计算公式不再赘述。

这就是半离散K-T格式，具体的minmod斜率限制器可参见论文原文。斜率限制器的目的是使得此二阶格式TVD，在间断解处退回一阶格式。

半离散格式只完成了空间离散，时间离散可使用TVD-龙格库塔法实现。

KURGANOV A, TADMOR E. New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations[J]. Journal of Computational Physics, 2000, 160(1): 241-282. ↩︎

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/131614.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！