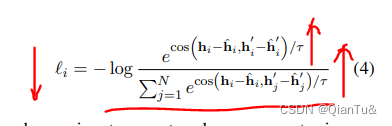深度材料感知跨光谱立体匹配

摘要

跨光谱成像对识别和检测任务很有帮助。通常，多个相机用于跨光谱成像，因此需要图像对齐或双目系统中的视差估计。多相机跨光谱系统逐渐被嵌入到有源RGB-D设备中（例如Kinect和iPhone X中的RGB-NIR相机）。因此，立体匹配提供了在没有主动投影仪的情况下获得深度的机会。然而，由于大的外观差异，匹配来自不同光谱带的图像非常具有挑战性。

• 本文开发了一种基于深度学习的方法，能同时进行跨光谱图像变换和视差估计。

• 在视差预测网络中使用了材料感知损失函数，用于处理具有不可靠匹配的区域，例如光源、挡风玻璃和光滑表面。

• 本文的方法采用无监督学习。

• 构建数据集。为了评估本文的方法，使用车载RGB-NIR立体系统，在一个城市内和周围一系列区域，收集了13.7小时的视频数据。

• 实验结果表明，该方法具有较强的性能和并能达到实时性。

1.介绍

跨光谱成像广泛应用于图像处理和计算机视觉领域：

• 近红外（NIR）、短波红外（SWIR）、中波红外（MWIR）图像能够帮助RGB图像进行人脸识别。

• RGB-NIR图像对用于阴影检测、场景识别和场景推理。

• NIR图像能够对彩色图像进行增强和去雾。

• 蓝色荧光和紫外光图像有助于皮肤表面重建。

• 彩色与热红外图像有助于行人检测。

⭐️动机⭐️

• 多相机-多光谱系统在现代设备中越来越常见（Kinect、iPhone X），由于大多数跨光谱算法需要对齐的图像作为输入，所以跨光谱对齐问题变得至关重要，然而在硬件中使用分束器对齐图像是不切实际的，因为这样会导致显著的光损失，进而需要更长的曝光时间，导致动态模糊。

• 立体匹配可以解决这个问题，先从校正的图像对中估计视差，然后根据获得的视差，通过图像变换得到对齐的图像。立体匹配还可以在没有主动光的情况下获得深度，有助于像检测和跟踪这样的任务。

⭐️挑战⭐️

由于成像光谱段不同，带来的巨大外观差异。

⭐️方法⭐️

采用两个无监督网络，同时进行视差估计和光谱变换。

• 视差估计网络（DPN）

• 光谱转换网络（STN）

损失函数由NIR图像和伪NIR图像的重投影和匹配关系构建。

DPN和STN能应对大部分场景，但是具有某些材料的区域匹配结果不可靠，如光源、玻璃和光滑表面，为了解决这些问题，采用一个材料识别网络（DeepLab）识别出不可靠的区域，然后利用上下文信息对这些区域进行视差推理。

DPN损失根据材料概率和预测的视差评估像素置信度，并利用置信度加权平滑技术将更多梯度反向传播到较低置信度像素。

⭐️数据集⭐️

• 13.7h的RGB-NIR立体对视频帧。

• 在图像的子集上标注了材料分割标签，来训练材料识别网络（DeepLab）。

• 在测试子集上标记稀疏视差用于评估。

2.相关工作

跨模态立体匹配

跨模态立体匹配的关键是计算不同成像模态之间的不变量。

• Chiu等人提出了基于线性通道结合的跨模态自适应方法

• Heo等人提出了一种对不同光照和颜色鲁棒的相似性度量

• Heo等人还提出了一种辐射变化下联合生成彩色一致立体图像和视差方法

• Pinggera等人表明HOG特征有助于可见光-热红外匹配

• Shen等人提出了一种具有鲁棒选择性归一化互相关的两阶段方案

• Kim等人设计了一个基于自相似性的描述符，并将其扩展为深度学习版本 🚀对比方法🚀

• Jeon等人提出了一种在弱光条件下补偿辐射差的彩色-单色匹配方法

这些方法基于特征或区域匹配而没有材料感知，并且对于诸如灯、玻璃或光滑表面的材料是不可靠的

无监督深度估计

无监督深度估计CNN通常用平滑先验和重投影误差来训练。

• Garg等人提出了基于Taylor展开和粗-细训练的单目方法

• Godard等人提出了具有左右一致性的单目深度网络 🚀参考方法🚀

• Zhou等人提出了一种基于运动网络的深度和摄像机姿态预测方法

• Zhou等人提出了一种通过选择可信匹配和训练数据的立体匹配方法

• Tonioni等人表明表明深度立体匹配模型可以用传统立体算法的输出进行微调

所有这些方法只处理RGB图像而不是跨光谱图像，没有考虑困难的非朗伯材料

3.同时预测视差和转换光谱

3.1 模型总览

本文方法包含两个无监督网络，分别为视差预测网络DPN和光谱转换网络STN。

• DPN采用Godard提出的结构，输入为RGB-NIR立体对 { I C l , I N r } \{I^{l}_{C}, I^{r}_{N}\} {ICl​,INr​}，输出为左右视差 { d l , d r } \{d^l, d^r \} {dl,dr}。

• STN输入为RGB左图$I_C^l$，输出伪NIR图像$I_{pN}^l$

两个网络的损失函数主要由重投影误差构成。

重投影左图${\tilde{I}}_N^l=\omega (I_N^r,-d^l)$，重投影右图${\tilde{I}}_{pN}^r=\omega (I_{pN}^l,d^r)$。

然后重投影左图${\tilde{I}}_N^l$和伪NIR左图$I_{pN}^l$计算重投影误差，重投影右图${\tilde{I}}_{pN}^r$和NIR右图$I_N^r$计算重投影误差。

$\tilde{I}(x,y)=\omega (I,d)(x,y)=I(x+d(x,y),y)$为重投影变换

解释${\tilde{I}}_N^l,{\tilde{I}}_{pN}^r$的计算公式：立体图像对中，左图像的对应点x坐标偏右（偏大）。以重投影左图为例，理论上重投影左图在(x,y)处的像素值，对应在NIR右图中偏左（x坐标值偏小）的点，即(x-d(x,y),y)。

3.2 视差估计网络

网络结构可以参考Godard，这里详细解读损失函数，它由三部分组成：

• $L_v$：视图一致性（view consistency）项

• $L_a$：对齐（alignment）项

• $L_s$：平滑（smoothness）项

DPN的总体损失函数：

$$L_{DPN}={\lambda }_v(L_v^l+L_v^r)+{\lambda }_v(L_a^l+L_a^r)+{\lambda }_s(L_s^l+L_s^r)\text{\hspace{1em}(1)}$$

具体来看:

⭐️视图一致性项$L_v^l$描述了左右视差图的一致性：

$$L_v^l=\frac{1}{N}\sum _{p\in \Omega }|d^l(p)-\omega (d^r,-d^l)(p)|\text{\hspace{1em}(2)}$$

N为像素总数，$\Omega$为像素坐标空间，p为某一像素点

⭐️对齐项$L_a^l$描述了伪NIR左图像$I_{pN}^l$和NIR右图像$I_N^r$之前的结构和亮度对齐：

$$L_a^l=\frac{1}{N}\sum _{p\in \Omega }(\alpha \delta (I_{pN}^l,{\tilde{I}}_N^l)(p)+(1-\alpha )|I_{pN}^l(p)-{\tilde{I}}_N^l)(p)|)\text{\hspace{1em}(3)}$$

$\delta (I_1,I_2)$为结构相似性SSIM，$\alpha =0.85$

⭐️平滑项$L_s^l$进行边缘感知，允许边缘存在不连续视差。

$$L_s^l=\frac{1}{N}\sum _{p\in \Omega }((|\frac{\partial d^l}{\partial x}|e^{-|S_x\ast I_C^l|}+|\frac{\partial d^l}{\partial y}|e^{-|S_y\ast I_C^l|})(p))\text{\hspace{1em}(4)}$$

$S_x,S_y$为Sobel算子，经过滤波的RGB彩色图片被平均为单通道图片。

3.3 光谱转换网络

RGB-NIR相机经过辐射测量标定，可以得到下面两种参数

• 白平衡增益：红色增益$g_R$、蓝色增益$g_B$。

• 曝光时间：$\Delta t_C$和$\Delta t_N$。

光谱转换网络STN通过局部滤波、白平衡和曝光校正，将彩色左图转换为伪近红外左图。

设${\mathcal{G}}_{{\theta }_1}$为白平衡操作，${\theta }_1$为可学习参数；${\mathcal{F}}_{{\theta }_2}^{(p)}$为滤波操作，对每个位置p都有对应的滤波参数${\theta }_2$；转换公式为：

$$I_{pN}^l=\frac{\Delta t_N}{\Delta t_C}{\mathcal{G}}_{{\theta }_1}(g_R,g_B){\mathcal{F}}_{{\theta }_2}^{(p)}(I_C^l(p))\text{\hspace{1em}(5)}$$

• ${\mathcal{G}}_{{\theta }_1}$是一个一层神经网络用于学习参数${\theta }_1=({\theta }_{11},{\theta }_{12},{\theta }_{13})$，激活函数为sigmoid。

$${\mathcal{G}}_{{\theta }_1}(g_R,g_B)=\beta h(\frac{{\theta }_{11}}{g_R}+\frac{{\theta }_{12}}{g_B}+{\theta }_{13})\text{\hspace{1em}(6)}$$

$\beta =2$是最大白平衡增益

• ${\mathcal{F}}_{{\theta }_2}^{(p)}$计算彩色图像R、G、B三通道的加权和，每个位置p的权重不一样。

$${\mathcal{F}}_{{\theta }_2}^{(p)}(I_C^l(p))={\theta }_{21}(p)I_R^l(p)+{\theta }_{22}(p)I_G^l(p)+{\theta }_{23}(p)I_B^l(p)\text{\hspace{1em}(7)}$$

$I_R^l,I_G^l,I_B^l$为彩色图的三通道分量，权重${\theta }_2(p)=({\theta }_{21}(p),{\theta }_{22}(p),{\theta }_{23}(p))$由一个滤器波生成网络（FGN）预测得到。

为了防止STN学习视差，本方法使用对称CNN作为FGN。因此，FGN对每个像素周围的左右部分有相同的处理，并且对输入进行移位操作，因此不学习视差。

• FGN的结构和DPN的结构相同，它预测RGB-to-NIR滤波器：

• STN的损失函数为NIR和pNIR的匹配误差：

$$L_{STN}=\frac{1}{N}\sum _{p\in \Omega }(|I_{pN}^l(p)-{\tilde{I}}_N^l(p)|+|I_N^r(p)-{\tilde{I}}_{pN}^r(p)|)\text{\hspace{1em}(8)}$$

4.将材料感知置信度引入视差预测网络

虽然DPN和STN在许多场景下都有较好的效果，但是某些材料会导致不可靠匹配匹配结果，如光源、玻璃和光滑表面等。因为这些材料具有很大的光谱成像差异。

• 不能通过匹配分数和视图一致性判断匹配结果的可靠性。

• 光源在RGB和NIR图中的大小不同，因此边缘的匹配并不可靠。

• 透射或反射的场景预测的视差与实际物理表面并不匹配。

本文的目标是将材料感知置信度估计和DPN的损失韩式相融合。提出了两种新的技术：

• 使用一种新的置信度加权平滑技术将视差从可靠区域传播到不可靠区域。

• 通过创建特定材料的对齐和平滑损失，将DPN损失函数扩展为材料感知DPN损失函数。

4.1 置信度加权视差平滑

平滑技术是一种在不可靠区域推理视差的常用方法。然而，平滑度损失允许不可靠区域通过迫使它们共享相似的视差来误导可靠部分。

置信度加权视差平滑技术，利用可靠的视差来监督不可靠的视差。我们改变平滑损失的反向传播行为，使得它可以嵌入到DPN损失中。

考虑两个临近像素$p_1$和$p_2$，他们的预测视差值为$d_1$和$d_2$。$L_1$平滑损失为$L=|d_1-d_2|$。设$W$为DPN的所有参数，那么就有$\frac{\partial L}{\partial W}=\frac{\partial L}{\partial d_1}\frac{\partial d_1}{\partial W}+\frac{\partial L}{\partial d_2}\frac{\partial d_2}{\partial W}$。假设$p_1$是可信，而$p_2$不可靠。我们希望$d_2$随着$d_1$变化，而并不改变$d_1$。

• 设$\chi (\cdot )$为停止梯度算子（比如PyTorch中的detach)在向前传递中充当身份映射，但在反向传递中阻止梯度通过它反向传播。设置信度感知损失函数$L=|\chi (d_1)-d_2|$，能够防止梯度通过$d_1$反向传播。当反向传播时，直接令$\frac{\partial L}{\partial d_1}=0$，即$\frac{\partial L}{\partial W}=\frac{\partial L}{\partial d_2}\frac{\partial d_2}{\partial W}$，并且它也可以扩展为“平滑”版本。

• 总的来说，让$p_1$和$p_2$具有置信度$c_1$和$c_2$。我们定义相关置信度$r_1=\frac{c_1}{c_1+c_2}$，$r_2=1-r_1$。

• 最终置信度加权损失函数为$L=r_1|\chi (d_1)-d_2|-r_2|d_1-\chi (d_2)|$

在实际应用中，考虑视差图$d(x,y)$及其已知的置信度$c(x,y)$。通过定义x和y方向上的邻域像素，给出了置信度的详细表达式。x方向上的相对置信度$r^{+}$和$r^{-}$为：

$$r^{+}(x,y)=\chi (\frac{c(x+1,y)}{c(x+1,y)+c(x-1,y)})\text{\hspace{1em}(9)}$$

x方向的置信度加权$L_1$平滑损失函数为：

$$L_x(d,c)(x,y)=r^{+}(x,y)|\frac{\chi (d(x+1,y))-d(x-1,y)}{2}|+r^{-}(x,y)|\frac{d(x+1,y)-\chi (d(x-1,y))}{2}|\text{\hspace{1em}(10)}$$

$r^{+},r^{-}$是相对置信度，$\chi ()$防止置信度高的视差进行梯度反向传播。
y方向的置信度加权平滑损失也是同样的原理。

完整的置信度加权平滑损失函数为：

$$L_{cs}(d,c)=L_x(d,c)+L_y(d,c)\text{\hspace{1em}(11)}$$

4.2 材料感知损失函数

使用DeepLab识别不可靠区域。在训练DPN和STN网络之前单独训练DeepLab网络。

有8个种类的材料：$\mathcal{M}=${光源，玻璃，光滑表面，植物，皮肤，衣服，背包，常见物品}

"常见物品"表示不属于这些特殊材料的其他材料，令${\mathcal{M}}^U$表示不可靠材料子集。

立体对作为DeepLab网络的输入，输出为左右图中每个像素属于材料m的概率 { μ m l ( p ) , μ m r ( p ) } \{\mu^{l}_{m}(p),\mu^{r}_{m}(p)\} {μml​(p),μmr​(p)}。

引入材料特定的对齐损失$L_{a,m}^l$和平滑损失$L_{s,m}^l$。重写公式（1）：

$$L_{DPN}={\lambda }_v(L_v^l+L_v^r)+\sum _{m\in \mathcal{M}}{\lambda }_{a,m}(\frac{1}{N}\sum _{p\in \Omega }({\mu }_m^l(p)L_{a,m}^l(p)+{\mu }_m^r(p)L_{a,m}^r(p)))+\sum _{m\in \mathcal{M}}{\lambda }_{s,m}(\frac{1}{N}\sum _{p\in \Omega }({\mu }_m^l(p)L_{s,m}^l(p)+{\mu }_m^r(p)L_{s,m}^r(p)))\text{\hspace{1em}(12)}$$

对于可靠的材料，对齐和平滑项依然使用公式（3）和公式（4）；对于不可靠的材料使用置信度加权平滑损失函数。

接下来描述如何根据${\mu }_m^l,{\mu }_m^r$计算公式（11）中的置信度c。

4.3 不可靠材料损失项示例

定义不可靠材料 M U = { ′ 光 源 ′ , ′ 玻 璃 ′ , ′ 光滑表 面 ′ } \mathcal{M}^U=\{'光源','玻璃','光滑表面'\} MU={′光源′,′玻璃′,′光滑表面′}，同时给出它们的损失项。

⭐️光源

驾驶场景中的尾灯、刹车灯、公交路线指示灯和车头灯等光源会导致不可靠匹配。

• 对齐损失项：光源部分在RGB和NIR图像中的大小不一致，本身就没有对齐，因此计算对齐损失意义不大，所以设对齐损失项$L_{a,light}^l=0$。

• 平滑损失项：假设光源区域和临近非光源区域的视差一致，置信度$c^l=1-{\mu }_{light}^l$，光滑损失项有：

$$L_{s,light}^l=L_{cs}(d^l,1-{\mu }_{light}^l)\text{\hspace{1em}(13)}$$

⭐️ 玻璃

玻璃既能反射也能透射。

• 对齐损失项：同样的，玻璃在RGB和NIR图像中也是不对齐的，因此令$L_{a,glass}^l=0$。

• 平滑损失项：像上面的图中显示的，普通材料通过玻璃反射或者透射的距离都要比实际距离要大。因此，可以在相近的场景中，分配更高的置信度给视差较大的区域。假设玻璃材料只由’玻璃‘，’光滑面‘和’普通材料‘支撑，它的置信度$c^l=({\mu }_{common}^l+{\mu }_{glass}^l+{\mu }_{glossy}^l)e^{\frac{d^l}{\sigma }}$，那么平滑损失项为：

$$L_{s,glass}^l=L_{cs}(d^l,({\mu }_{common}^l+{\mu }_{glass}^l+{\mu }_{glossy}^l)e^{\frac{d^l}{\sigma }})\text{\hspace{1em}(14)}$$

深度与视差成反比，视差越大深度越小，因此置信度越大，$\sigma =0.005$是超参数。

⭐️ 光滑表面

光滑表面具有很复杂的光谱反射。

• 对齐损失项：考虑到它依然有许多可靠的匹配，故采用普通材料的对齐损失项，也就是公式（3）

• 平滑损失项：由于反射的场景具有更小的视差，采用玻璃材料的平滑损失项，也就是公式（14）。

5.RGB-NIR立体数据集

• 硬件参数：一个RGB相机和一个NIR相机组成基线为56mm的车载立体系统，分辨率为1164×858

• 曝光条件：在20Hz的自动曝光算法中，在短、中、长曝光之间交替进行。三种曝光水平均匀分布。

• 数据量：一共13.7h,被分为12个视频。

• 拍摄场景：校园路，高速公路，乡下，公园和住宅区；包括晴天，多云和夜晚；同时包括多种材料，如光源，玻璃，光滑表面，植物，皮肤，衣服和背包等。

• 拍摄条件：70%的数据都是在可靠的GPS和车辆状态（速度、车辆姿态、转向半径和行驶距离）下采集的。

在实验中，所有的图片分辨率被缩放到582×429

• 标签：在中间曝光图像的子集添加材料和视差标签；3600帧标有8类材料分割标签；在所有8种材料的2000个测试图像上的5030个稀疏点有视差标签。

• 分组：视频分为两组，用于训练（8个视频）和测试（4个视频）。

没有使用深度传感器，因为它们经常在玻璃和光源上失效。

6.实验结果

⭐️ 参数

DPN预测视差和图像宽度之间的比率。缩放因子为$\eta$：

• DPN的$\eta =0.008$

• STN的$\eta =\frac{1}{3}$

对于所有的材料，视图一致性权重和对齐权重分别是:

• ${\lambda }_v=2$

• ${\lambda }_a=1$

对于平滑权重${\lambda }_s$

光源	玻璃	光滑表面	其他
3000	1000	80	25

⭐️ 训练与测试

• DeepLab网络先在ImageNet，COCO和Pascal VOC数据集上训练，再进行微调。

• DPN和STN使用Adam优化器从40000个中等曝光的图像中训练网络。

批次为16，学习率为0.00005；
前4轮训练不使用材料感知损失；之后使用材料感知损失至少训练12轮；
测试只需要使用DPN；
负视差直接置为0；

⭐️ 对比方法

• CMA

• ANCC

• DASC

在DASC中，SIFT流搜索受对极几何约束，来获得整个图像的视差。

对比指标包括：视差均方根误差，执行时间和定性结果。

• 定量结果

• 定性结果

⭐️ 消融实验

尝试3种网络结构：

• 只有RGB作为DPN的输入

• RGB三通道图像取平均作为STN

• STN中使用对称CNN

“w/o"表示"without”
表2显示，总体而言，完整方法优于其他选择
表2还显示了置信度平滑是有用的。

表2和图8显示忽略光源、玻璃或光滑表面将会在这些区域预测失败，在其他材料上也有小的波动。这意味着特定材料损失发挥了它的作用。

7.总结与讨论

• 提出了一种基于深度学习的无深度监督跨光谱立体匹配方法

• 同时预测视差并将RGB图像转换为NIR图像。

• 利用对称CNN来分离几何和光谱差异。

• 引入材料感知和置信度加权平滑度来处理由光源、玻璃和光滑表面引起的问题。

• 建立了一个具有挑战性案例的大型RGB-NIR立体数据集进行评估。

我们的方法优于比较的方法，特别是在具有挑战性的材料上，尽管它在一些具有较大的光谱差异的服装、阴影边缘和暗噪声区域上效果不好。

重新设计损失函数可能有助于解决这些问题。未来，可以把工作扩展到其他光谱（SWIR、MWIR、热光谱）和从移动消费设备获得的数据。